BP神经网络原理与应用-基于电影评分预测案例

BP神经网络简介

BP神经网络（Back Propagation Neutral Network）是1986年由Rumelhart和McCelland为首的科学家小组提出，是一种按误差逆传播算法训练的多层前馈网络，是目前应用最广泛的神经网络模型之一。BP神经网络使用最速下降法，通过反向传播不断调整网络的权值和阈值，是网络的误差平方和最小，从而实现模式识别等功能。

BP神经网络组成的结构包括有输入层、隐含层以及输出层，而每一层都有一定个数的神经元来接收、处理并输出数据。输入层主要负责接收输入参数，输入层神经元的数量取决于模型的输入特征数量，隐含层的层数以及每层所包含的神经元数量取决于对模型精度以及训练速度的要求，输出层神经元的数量取决于模型所要求的输出特征个数。

BP神经网络的训练在于对网络中各参数（神经元之间的权重以及阈值）的调整，使得整个模型误差最小。研究认为具有至少三层（单隐含层）的BP神经网络，考虑权重以及阈值的存在，可以无限逼近于任何有理函数。因此，不同于传统的多元线性回归方法，BP神经网络在解决非线性问题方面有着很好的优势，如异或（XOR）问题。

BP神经网络数学原理

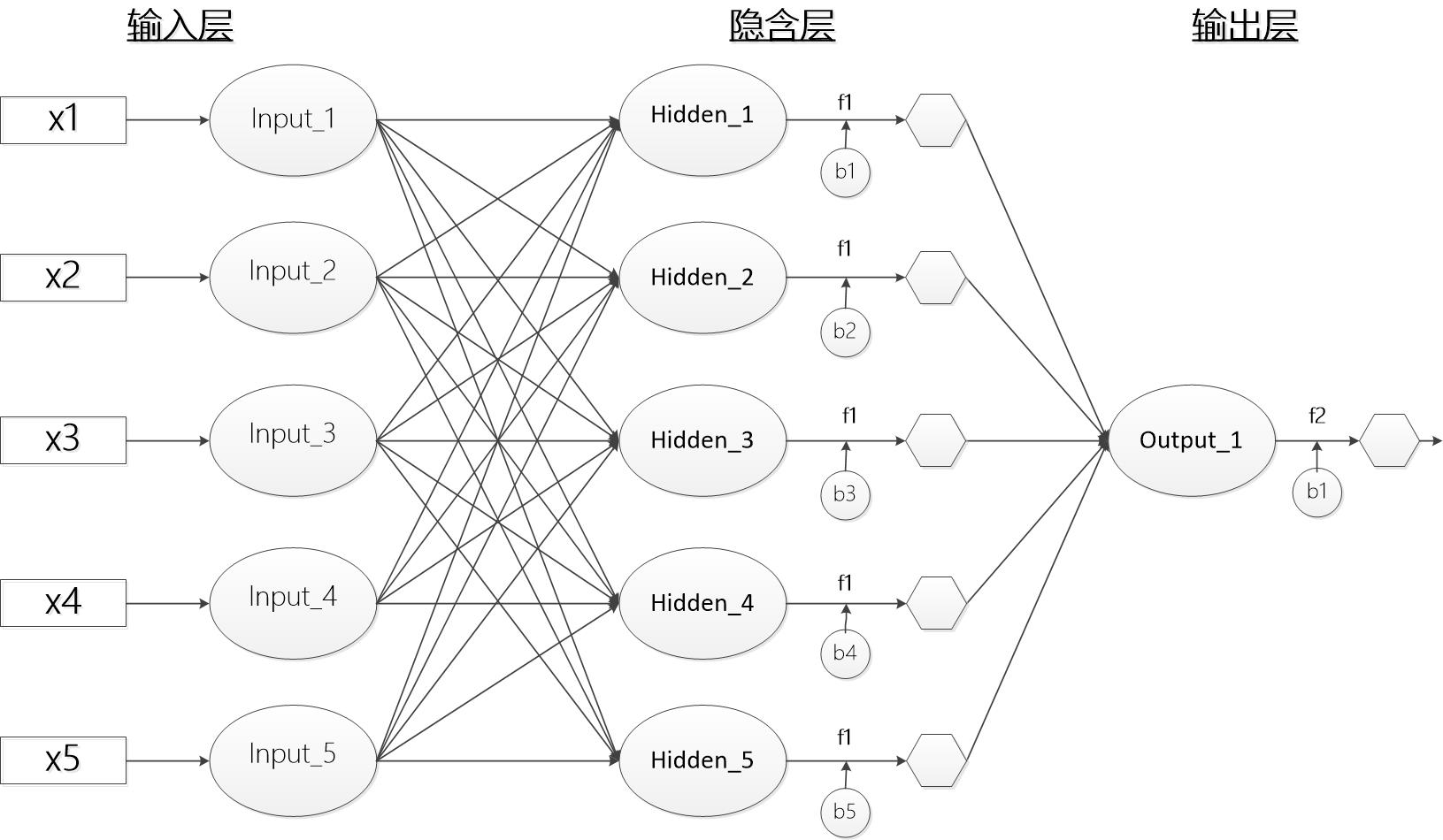
BP神经网络结构图

上图显示了一个基本的BP神经网络构造图，其中包括5个输入节点（特征），5个隐含层节点，以及1个输出层节点

BP神经网络数学原理

• 本部分数学公式按照下部分案例进行讲解，设置输入层节点5个，隐含层节点5个，输出层节点1个
• 本案例中所有的激活函数，均采用$tan()$函数，没有采用不同的激活函数

1.参数定义

• 输入层输入值：$x_i(i为输入层节点个数)$->$\{x_1,x_2,x_3, x_4, x_5\}$
• 隐含层净值：$net_{Hj}(j表示隐含层节点个数)$->$\{net_{H1},net_{H2},net_{H3},net_{H4},net_{H5}\}$
• 隐含层激活值：$act_{Hj}$-> { actH1,actH2,actH3,act