-
导数
导数(Derivative)是
微积分中的重要基础概念。当函数y=f(x)的
自变量x在一点x
0上产生一个增量Δx时,函数输出值的增量Δy与自变量增量Δx的比值在Δx趋于0时的
极限a如果存在,a即为在x
0处的导数,记作f'(x
0)或df(x
0)/dx。
目录
起源
大约在1629年,法国数学家
费马研究了作曲线的切线和求函数
极值的方法;1637年左右,他写一篇手稿《求最大值与最小值的方法》。在作切线时,他构造了
差分f(A+E)-f(A),发现的因子E就是我们所说的导数f'(A)。
[2]
发展
17世纪生产力的发展推动了自然科学和技术的发展,在前人创造性研究的基础上,大数学家
牛顿、
莱布尼茨等从不同的角度开始系统地研究微积分。牛顿的微积分理论被称为“流数术”,他称变量为流量,称变量的变化率为
流数,相当于我们所说的导数。牛顿的有关“流数术”的主要著作是《求曲边形面积》、《运用无穷多项方程的计算法》和《流数术和
无穷级数》,流数理论的实质概括为:他的重点在于一个变量的函数而不在于多变量的方程;在于自变量的变化与函数的变化的比的构成;最在于决定这个比当变化趋于零时的极限。
[2]
成熟
1823年,
柯西在他的《无穷小分析概论》中定义导数:如果函数y=f(x)在变量x的两个给定的界限之间保持连续,并且我们为这样的变量指定一个包含在这两个不同界限之间的值,那么是使变量得到一个无穷小增量。19世纪60年代以后,
魏尔斯特拉斯创造了ε-δ语言,对微积分中出现的各种类型的极限重加表达。导数的定义也就获得了今天常见的形式。
微积分学理论基础,大体可以分为两个部分。一个是
实无限理论,即无限是一个具体的东西,一种真实的存在;另一种是
潜无限理论,指一种意识形态上的过程,比如无限接近。
就数学历史来看,两种理论都有一定的道理。其中实无限用了150年,后来极限论就是现在所使用的。
就数学历史来看,两种理论都有一定的道理。其中实无限用了150年,后来极限论就是现在所使用的。
光是电磁波还是粒子是一个物理学长期争论的问题,后来由波粒二象性来统一。微积分无论是用现代极限论还是150年前的理论,都不是最好的方法。
设
函数y=f(x)在点x
0的某个
邻域内有定义,当自变量x在x
0处有增量Δx,(x
0+Δx)也在该邻域内时,相应地函数取得
增量Δy=f(x
0+Δx)-f(x
0);如果Δy与Δx之比当Δx→0时
极限存在,则称函数y=f(x)在点x
0处可导,并称这个极限为函数y=f(x)在点x
0处的导数记作
①f'(x
0) ;
②y'│
x=x0 ;
③
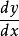 │
x=x0, 即
│
x=x0, 即
需要指出的是:
两者在数学上是等价的。
导函数
如果函数y=f(x)在开区间内每一点都可导,就称函数f(x)在区间内可导。这时函数y=f(x)对于区间内的每一个确定的x值,都对应着一个确定的导数值,这就构成一个新的函数,称这个函数为原来函数y=f(x)的
导函数,记作y'、f'(x)、dy/dx或df(x)/dx,简称导数。
几何意义
函数y=f(x)在x
0点的导数f'(x
0)的几何意义:表示函数曲线在点P
0(x
0,f(x
0))处的切线的斜率(导数的几何意义是该函数曲线在这一点上的切线斜率)。
简单函数
这里将列举14个
基本初等函数的导数。
| 函数 | 原函数 | 导函数 |
|---|---|---|
|
(即
常数)
|
|
|
| 指数函数 |
|
|
| 幂函数 |
|
|
| 对数函数 |
|
|
| 正弦函数 |
|
|
| 余弦函数 |
|
|
| 正切函数 |
|
|
| 余切函数 |
|
|
| 正割函数 |
|
|
| 余割函数 |
|
|
| 反正弦函数 |
|
|
| 反余弦函数 |
|
|
| 反正切函数 |
|
|
| 反余切函数 |
|
|
|
|
|
复杂函数
y=f(x)的反函数是x=g(y),则有y'=1/x'。
复合函数对自变量的导数,等于已知函数对中间变量的导数,乘以中间变量对自变量的导数(称为
链式法则)。
4、变限积分的求导法则:
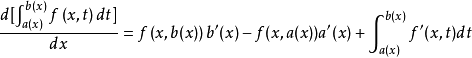
(a(x),b(x)为子函数)
导数的计算
计算已知函数的导函数可以按照导数的定义运用变化比值的极限来计算。在实际计算中,大部分常见的解析函数都可以看作是一些简单的函数的和、差、积、商或相互复合的结果。只要知道了这些简单函数的导函数,那么根据导数的求导法则,就可以推算出较为复杂的函数的导函数。
导数的求导法则
由基本函数的和、差、积、商或相互复合构成的函数的导函数则可以通过函数的求导法则来推导。基本的求导法则如下:
1、求导的线性:对函数的线性组合求导,等于先对其中每个部分求导后再取线性组合(即①式)。
2、两个函数的乘积的导函数:一导乘二+一乘二导(即②式)。
3、两个函数的商的导函数也是一个分式:(子导乘母-子乘母导)除以母平方(即③式)。
4、如果有复合函数,则用链式法则求导。
高阶求导
高阶导数
的求法
1.直接法:由高阶导数的定义逐步求高阶导数。
一般用来寻找解题方法。
2.高阶导数的运算法则:
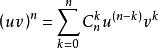 (
二项式定理)
(
二项式定理)
3.间接法:利用已知的高阶导数公式,通过
四则运算,变量代换等方法。
注意:代换后函数要便于求,尽量
靠拢已知公式求出阶导数。
口诀
为了便于记忆,有人整理出了以下口诀:
-
常为零, 幂降次
-
对倒数( e为底时直接倒数,a为底时乘以1/lna )
-
指不变(特别的,自然对数的指数函数完全不变,一般的指数函数须乘以lna )
-
正变余,余变正
-
切割方(切函数是相应割函数(切函数的倒数)的平方 )
-
割乘切,反分式
单调性
⑴若导数大于零,则单调递增;若导数小于零,则单调递减;导数等于零为函数
驻点,不一定为
极值点。需代入驻点左右两边的数值求导数正负判断单调性。
⑵若已知函数为递增函数,则导数大于等于零;若已知函数为递减函数,则导数小于等于零。
⑵若已知函数为递增函数,则导数大于等于零;若已知函数为递减函数,则导数小于等于零。
根据
微积分基本定理,对于可导的函数,有:
如果函数的导函数在某一区间内恒大于零(或恒小于零),那么函数在这一区间内单调递增(或单调递减),这种区间也称为函数的单调区间。导函数等于零的点称为函数的驻点,在这类点上函数可能会取得极大值或极小值(即极值可疑点)。进一步判断则需要知道导函数在附近的符号。对于满足的一点,如果存在使得在之前区间上都大于等于零,而在之后区间上都小于等于零,那么是一个极大值点,反之则为极小值点。
x变化时函数(蓝色曲线)的切线变化。函数的导数值就是切线的斜率,绿色代表其值为正,红色代表其值为负,黑色代表值为零。
凹凸性
可导函数的凹凸性与其导数的单调性有关。如果函数的导函数在某个区间上单调递增,那么这个区间上函数是向下凹的,反之则是向上凸的。如果二阶导函数存在,也可以用它的正负性判断,如果在某个区间上恒大于零,则这个区间上函数是向下凹的,反之这个区间上函数是向上凸的。曲线的凹凸分界点称为曲线的
拐点。
双曲函数
均能较快捷地求得结果。
对于
 有更直接的求导方法。
有更直接的求导方法。
下面对
 进行求导
进行求导
由
指数函数定义可知,y>0
等式两边取
自然对数
等式两边对x求导,注意y是y对x的
复合函数
幂函数
幂函数同理可证。
导数说白了它其实就是曲线一点切线的斜率,函数值的变化率。
上面说的分母趋于零,这是当然的了,但不要忘了分子也是可能趋于零的,所以两者的比就有可能是某一个数,如果分子趋于某一个数,而不是零的话,那么比值会很大,可以认为是
无穷大,也就是我们所说的导数不存在。
设y=x/x,若这里让x趋于零的话,分母是趋于零了,但它们的比值是1,所以极限为1。
连续不可导的曲线
例如,
魏尔斯特拉斯函数(Weierstrass function)就是一类处处连续而处处不
可导的实值函数。魏尔斯特拉斯函数是一种无法用笔画出任何一部分的函数,因为每一点的
导数都不存在,画的人无法知道每一点该朝哪个方向画。魏尔斯特拉斯函数的每一点的
斜率也是不存在的。魏尔斯特拉斯函数得名于十九世纪的德国数学家
卡尔·魏尔斯特拉斯(Karl Theodor Wilhelm Weierstrass,1815–1897)。历史上,魏尔斯特拉斯函数是一个著名的数学反例。魏尔斯特拉斯之前,数学家们对函数的连续性认识并不深刻。许多数学家认为除了少数一些特殊的点以外,连续的函数曲线在每一点上总会有斜率。魏尔斯特拉斯函数的出现说明了所谓的“病态”函数的存在性,改变了当时数学家对连续函数的看法。
科学应用
导数与物理,几何,代数关系密切:在几何中可求
切线;在代数中可求瞬时变化率;在物理中可求速度、加速度。
如一辆汽车在10小时内走了 600千米,它的平均速度是60千米/小时。但在实际行驶过程中,是有快慢变化的,不都是60千米/小时。为了较好地反映汽车在行驶过程中的快慢变化情况,可以缩短时间间隔,设汽车所在位置s与时间t的关系为:

那么汽车在由时刻t
0变到t
1这段时间内的平均速度是:

当 t
1无限趋近于t
0时,汽车行驶的快慢变化就不会很大,平均速度就近似等于t
0时刻的瞬时速度,因而就把此时的
极限 作为汽车在时刻t
0的瞬时速度,即
 ,这就是通常所说的速度。这实际上是由平均速度
类比到瞬时速度的过程 (如我们驾驶时的限“速” 指瞬时速度)。
[1]
,这就是通常所说的速度。这实际上是由平均速度
类比到瞬时速度的过程 (如我们驾驶时的限“速” 指瞬时速度)。
[1]
导数另一个定义:当x=x
0时,f'(x
0)是一个确定的数。这样,当x变化时,f'(x)便是x的一个函数,我们称他为f(x)(关于x)的导函数(derivative function),简称导数。
物理学、几何学、经济学等学科中的一些重要概念都可以用导数来表示。如:导数可以表示运动物体的瞬时速度和加速度(就直线运动而言,位移关于时间的
一阶导数是瞬时速度,
二阶导数是加速度),可以表示曲线在一点的
斜率,还可以表示经济学中的边际和弹性。
[1]
以上说的经典导数定义可以认为是反映局部
欧氏空间的函数变化。为了研究更一般的
流形上的
向量丛
截面(比如
切向量场)的变化,导数的概念被推广为所谓的“联络”。有了联络,人们就可以研究大范围的几何问题,这是微分几何与物理中最重要的基础概念之一。
2.导数为零的点不一定是
极值点。当函数为
常值函数,没有增减性,即没有
极值点。但导数为零。(导数为零的点称之为驻点,如果驻点两侧的导数的符号相反,则该点为极值点,否则为一般的驻点,如
 中f'(0)=0,x=0的左右导数符号为正,该点为一般驻点。)
中f'(0)=0,x=0的左右导数符号为正,该点为一般驻点。)
求导方法(定义法):
①求函数的增量
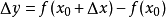 ;
;
②求平均变化率;
③取极限,得导数。








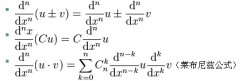
















 1361
1361

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








