【论】 The bike sharing rebalancing problem: Mathematical formulations and benchmark instances

The bike sharing rebalancing problem: Mathematical formulations and benchmark instances

@article{2014rebalancingmath,
title = {The bike sharing rebalancing problem: Mathematical formulations and benchmark instances},
journal = {Omega},
volume = {45},
pages = {7-19},
year = {2014},
issn = {0305-0483},
doi = {https://doi.org/10.1016/j.omega.2013.12.001},
url = {https://www.sciencedirect.com/science/article/pii/S0305048313001187},
author = {Mauro Dell'Amico and Eleni Hadjicostantinou and Manuel Iori and Stefano Novellani},
keywords = {Integer programming, Routing, Traveling salesman, Vehicle scheduling},
}

集锦

• 自行车共享再平衡问题是一个非常新且有趣的问题。
• 我们用四种公式对问题进行建模，并通过分支切割法解决它们。
• 我们提供了一组从现实世界的自行车共享系统中获得的基准实例。
• 广泛的计算结果表明了所提出算法的有效性

摘要

自行车共享系统提供了一种移动服务，通过该服务，位于城市地区不同站点的公共自行车可供共享。这些系统有助于获得更可持续的流动性并减少汽车运输造成的交通和污染。自 1965 年第一个自行车共享系统在阿姆斯特丹安装以来，此类应用程序的数量显着增加，以至于数百个系统现在在全球范围内运行。

在共享单车系统中，用户可以从车站取一辆自行车，用它完成一段旅程，然后把它留在一个车站，不一定是出发的那个。这种行为通常会导致某些站点变满而其他站点变空的情况。因此，一个平衡的系统需要在车站之间重新分配自行车。

在本文中，我们解决了共享单车再平衡问题 Bike sharing Rebalancing Problem(BRP)，在该问题中，使用一队有容量的车辆来重新分配自行车，以最大限度地降低总成本。这可以被视为一个特殊的单一商品取货和交付能力车辆路径问题。我们提出了这个问题的四个混合整数线性规划公式。值得注意的是，所提出的公式包括指数数量的约束，因此，开发了量身定制的分支切割算法来解决这些问题。

BRP 的数学公式首先使用从意大利雷焦艾米利亚市获得的数据进行了计算测试。我们的计算研究随后扩展到包括来自世界其他地区的自行车共享系统。从研究中获得的信息用于为 BRP 构建一组基准实例，我们在网络上公开了这些实例。对本文提出的分支切割算法进行了广泛的实验，并报告了所提出的数学公式的有趣计算比较。最后，强调了关于问题计算难度的几个见解。

1. Introduction

自行车共享系统提供一种移动服务，其中公共自行车可供共享使用。这些自行车位于遍布市区的车站。该系统的用户可以从车站取一辆自行车，用它去旅行，把它留在车站（不一定是出发车站），然后按使用时间付费。

这些系统是公共行政部门用来获得更可持续的机动性、减少交通和汽车运输造成的污染以及解决与近距离旅行相关的所谓最后一英里问题的重要工具。从 1965 年在阿姆斯特丹安装第一个自行车共享系统开始，它们的数量在接下来的几年里不断增加，到 2011 年仅在欧洲就达到了 400 多个系统，例如，参见 DeMaio [1] 和项目 OBIS [ 2 ]。在北美，自行车共享系统的实施始于 2008 年，参见 Pucher 等人。[3]，但据我们所知，它已经有 20 多个操作系统。正如 Shaheen 等人所讨论的那样，在世界其他地方，系统的数量正在以非常高的速度增长。[4].

车站由不同的插槽组成，每个插槽都有一辆自行车。在现代系统中，站点连接到互联网并实时显示每个插槽的占用状态。通过这种方式，用户可以很容易地检查可以在哪里取放自行车。持续监控系统的使用情况，收集的信息用于提高服务水平。

运营共享单车系统的成本可能差异很大（取决于系统本身、人口密度、服务区域和车队规模），对公共行政预算的影响是一致的。安装系统的设置成本包括购买自行车、停车位和车站的成本，以及用于操作设备的后端系统的成本，例如，参见 DeMaio [1 ]。日常运营成本包括维护、保险、可能的网站托管和电力，最重要的是，由于在站点之间重新分配自行车而产生的成本。事实上，在一天结束时，一些站点通常已满，而另一些站点则空无一人。

一个普遍采用的重新平衡规则是让每个站点只被部分占用，即在一个站点中应该总是有一些被自行车占用的槽位，以允许用户拿起它们，以及一些空闲槽位，以允许用户放下自行车在他们旅程的尽头。让我们假设在清晨在给定的自行车站出现所需的占用水平，然后由于用户的出行行为，自行车的数量可能会在一天中从所需的水平急剧变化。这通常发生在以丘陵地区为特征的城市中，例如，参见 Kaltenbrunner 等人。[5]，用户从位于山顶的车站乘坐自行车，将其留在山脚下，然后使用不同的交通工具返回。对于位于平坦地区的城市也很常见，其中一些站点在一天的不同时间有大量流入或流出。在下一节中，我们将报告在雷焦艾米利亚市（意大利）使用了七个月的系统分析结果。

重新定位Repositioning 通常是通过基于中央仓库的有能力的车辆来完成的，这些车辆从占用水平过高的站点提取自行车并将它们运送到占用水平过低的站点。通常，自行车缓冲区会存放在停车场，用于更灵活的重新分配。由此产生的决定如何安排车辆路线以便以最小成本执行重新分配的优化问题在文献中被称为自行车共享再平衡问题 Bike sharing Rebalancing Problem(BRP)，并且最近引起了该领域许多研究人员和从业者的兴趣。它可以建模为动态或静态优化问题。在静态版本中，拍摄车站占用水平的快照，然后用于规划重新分配。在动态版本中，考虑了系统的实时使用情况，随着时间的推移，一旦决策所需的信息被披露，重新分配计划可能会立即更新。

通常，静态重新平衡与在夜间执行的重新分配过程相关联，此时系统保持关闭或需求非常低，而动态重新平衡与白天运行的重新分配相关联，此时需求可能很高。在我们详细研究的真实案例中，重新分配是在夜间执行的，因此我们关注问题的静态版本。

在本文中，我们提供了几个贡献。在第 2 节中，我们通过分析旅行流量、用户行为和由此产生的车站占用水平，简要介绍了我们在雷焦艾米利亚市进行的真实案例研究。在第 3 节中，我们正式描述了 BRP 并讨论了相关文献。在第 4 节中，我们提出了四种混合整数线性规划(MILP) 公式来对问题进行建模。所有这些公式都涉及指数数量的约束，因此第 5 节介绍了我们为解决这些问题而实施的分支切割算法。我们在第 6 节中展示了大量基准实例，通过分析全球多个自行车系统的使用情况获得；我们在 Internet 上公开这些实例。分支切割算法的广泛计算结果在第 7 节中报告。最后，第 8 节给出了结论，并讨论了未来的研究方向。

2 . Data analysis of a real-world case 一个真实案例的数据分析

我们研究的第一个真实案例是雷焦艾米利亚的自行车共享系统，该城市位于意大利北部非常平坦的地区，拥有约 17 万居民。图1中描绘的系统非常小，现在有一个停车场（图中用0表示）、13个车站和大约100辆自行车。它全天运行，但在夜间保持关闭状态，这对于中小城市的自行车共享系统来说非常普遍。自行车的重新分配是在夜间进行的，通过一辆只访问每个站点一次的车辆。

图 1。雷焦艾米利亚 Reggio Emilia的自行车共享系统。车站用0表示。星号、圆圈和三角形分别代表第一组、第二组和第三组车站。

该市政府向我们提供了与该系统七个月使用情况相关的数据。它包含用户在考虑的时间段内执行的旅程列表，包括每次旅程的出发和到达时间和车站。对于每个站点，我们每天评估自行车的净流量，计算为流入量和流出量之间的差值。这给出了每个车站在一天开始时可用的自行车和一天结束时剩余的自行车之间的差异。然后，我们绘制了该时期内净流量的分布情况，见图2中的分布图。x轴给出差异$\Delta$每天到达和离开车站的时间间隔，y轴给出时间百分比$\Phi$（出现频率）这个数字出现在我们研究的整个时期。我们主要发现了类似正态分布的分布，如图2 (a) 所示的第 4 站，但也发现了第 5 站的双峰分布，见图2 (b)。在这两种情况下，在观察的大部分时间里，站点最终停放的自行车数量与当天开始时的数量不同，这支持了执行重新平衡操作的选择。

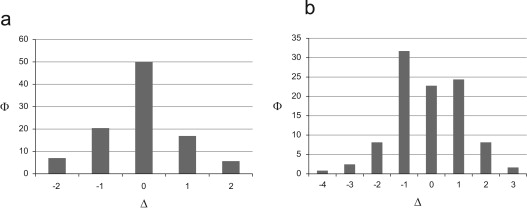
图 2。每天的自行车净流量，遵循 (a) 站点 4 的正态分布和 (b) 站点 5 的双峰分布 ($\Delta$,到达和离开之间的偏差；$\Phi$，出现频率）

此外，通过分析所有站点的每小时净流量，我们已经能够确定客户使用情况的不同可变性。因此，我们可以将站点分为三组，如图3所示。在此图中，x轴表示一天中的时间τ ， y轴表示七个月内进出车站的自行车累计数量ν 。进一步来说：

1. 第一组，见图3 (a)，在早上 7 点到 9 点之间有一个进入自行车的高峰，在下午 1 点到 3 点之间有一个较小的高峰。外出自行车的高峰出现在中午 12 点到下午 2 点和下午 4 点到 6 点之间。这些车站都位于市中心，只有一个车站位于医院附近（1、2、3、4、5 和 13 号车站）。这种用法很符合在市中心工作但住在外面的用户的行为。
2. 第二组与第一组互补，见图3 (b)。这些站点（6、7、8、9 和 12）位于所谓的停车换乘区，用户可以在这里停放汽车并继续骑公共自行车。
3. 第三组，见图3 ©，包含白天到达和离开遵循类似模式的站点。这些车站（10 号和 11 号）靠近全天使用的地方，例如火车站。

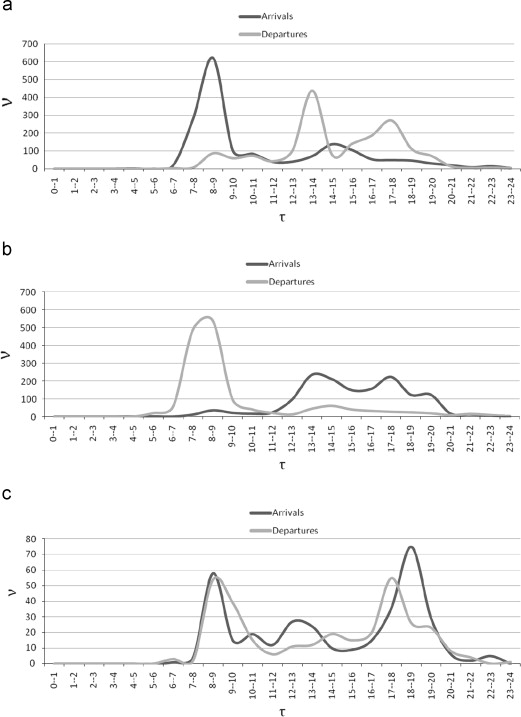
图 3。(a) 第一组、(b) 第二组和 © 第三组车站的典型每小时到达和离开（τ，一天中的小时；ν，累计到达或离开的自行车数量七个月内停止）。

更多关于自行车出行习惯的研究超出了本文的范围，因此有兴趣的读者可以参考相关文献。Vogel 和 Mattfeld [6]提出了自行车共享系统的商业模式。他们借助使用仿真工具解决的系统动力学方法对重新定位活动进行建模。他们得出的结论是，“在重新定位上花费更多的精力可以在客户满意度方面带来更好的企业绩效”。Kaltenbrunner 等。[5]使用当地自行车共享计划站点中的可用自行车数量，对巴塞罗那（西班牙）市区的人员流动数据进行分析。通过使用从运营商网站采样的数据，他们可以检测城市内的时间和地理流动模式。Lin 和 Yang [7]阐述了公共自行车共享系统的战略规划。这些作者提出了一个模型，试图确定自行车站点的数量和位置、用户的出行路径以及连接站点的自行车出行网络结构。

Souffriau 等人研究了最合适的自行车旅行的确定。[8]，针对东佛兰德斯（比利时）出现的一个问题，其动机是骑自行车的人在寻找一定长度的好路线时要处理的问题。他们提出了一个数学模型和一个元启发式算法。元启发式算法获得了良好的计算结果，然后被嵌入到基于网络的自行车路线规划器中。我们还提到 Boctor 等人在不同的背景下也面临类似的问题。[9]，谁研究了在加油站补给问题中分配车辆的行程。

3. Problem description and previous work 问题描述和之前的工作

我们得到了一个完整的有向图$G=(V,A)$，其中顶点集 V = { 0 , 1 , ⋯   , n } V=\{0,1,\cdots,n\} V={0,1,⋯,n}被划分为车站-顶点 0 和车站-顶点集 { 1 , 2 , ⋯   , n } \{1,2,\cdots,n\} {1,2,⋯,n}. 每个站点$i$都有一个请求$q_i$，可以是正的也可以是负的。如果那么$i$是一个拾取节点，其中$q_i$辆自行车应该被移除；如果那么$i$是一个交付节点，其中应该提供$q_i$辆自行车，对于 i ∈ V a ^ § 1 { 0 } i\in V_{â§^1}\{0\} i∈Va^§1​{0}. 从取货节点移除的自行车可以前往交付节点或返回仓库。提供给交付节点的自行车可以来自仓库或取货节点。一个由$m$辆容量为$Q$的相同车辆组成的车队可用于运输自行车。旅行成本$c_{ij}$与每个弧$arc(i,j)\in A$相关联.

BRP 涉及确定如何通过图表最多驾驶m辆车，目的是最小化总成本并确保不违反以下约束：
（i）每辆车执行一条从站点开始和结束的路线，（ ii) 每辆车从空车场开始，或者有一些初始负载（即，自行车数量从 0 到Q不等），（iii）每个站点只访问一次，并且访问它的车辆完全满足其请求，以及（iv）在车辆执行的路线中，被访问站点的请求加上初始负载的总和永远不会为负或大于Q。

在我们的研究中，每个请求$q_i$被计算为执行重新分配时出现在站点$i$ 的自行车数量与站点中最终所需配置中的自行车数量之间的差异。请注意，font color=coral>我们强制要求$q_i=0$的站点必须被访问，即使这意味着没有自行车必须在那里下车或上车。例如，当车辆的司机应该检查车站是否正常工作时，就会出现这种情况。<必须跳过具有空请求的站的情况可以通过在预处理阶段从顶点集合中移除那些站来简单地获得。

允许每辆车以部分自行车开始其路线这一事实扩大了可行的 BRP 解决方案的空间，并允许获得更灵活的重新分配计划。另请注意，我们不会将重新分配的自行车总数强加为空，因此站点上的自行车流量可能是正的也可能是负的。这种考虑对于模拟一些自行车进入或离开停车场进行维修的情况很有用。

在我们的例子中，旅行成本$c_{ij}$被计算为连接$i$和$j$ 的道路网络中路径的最短长度，对于$i,j\in V$. 在有向图上工作很重要，因为我们知道的所有自行车共享系统都位于城市地区，因此单行道通常对车辆在重新分配期间执行的路线选择有很大影响。

表1

BRP 属于范围广泛的取货和送货车辆路由问题Pickup and Delivery Vehicle Routing Problems(PDVRP)，其中车队用于将请求从站点和/或某些节点传输到站点和/或网络中的其他节点。具体来说，一些取件客户需要一定数量的货物由车辆取走，然后运到其他地方，而一些送货客户则需要一定数量的货物送到那里。BRP 概括了著名的容量车辆路径问题 Capacitated Vehicle Routing Problem (CVRP)，其中客户要么都是取货点，要么都是送货点，但不是两者兼而有之，因此它是一个强 NP-hard 问题。

Berbeglia 等人提出了 PDVRP 的详细审查和分类。[10]和 Parragh 等人。[11] , [12]。Battarra 等人提出了最近的调查。[13]涉及货物运输，Doerner 和 Salazar-González [14]涉及人员运输。按照 Berbeglia 等人介绍的符号。[10]，BRP 可以归类为多对多(M–M) 车辆路径问题Many-to-Many (M–M) vehicle routing problem,，其中一个请求有多个起点（在我们的案例中是取货站）和多个目的地（在我们的案例中是送货站）。

M-M PDVRP 类中最基本的问题可能是单一商品取货和送货旅行商问题 One-commodity Pickup and Delivery Traveling Salesman Problem(1-PDTSP)，它需要路由单个有能力的车辆以满足 M-M 请求。1-PDTSP 由 Hernández-Pérez 和 Salazar-González [15]正式引入，他们提出了数学公式和分支切割算法。为问题的对称和非对称版本给出了数学公式，并且基于二元变量$xij$的使用，如果使用边$arc(i,j)$，则取值为 1，否则为 0，非-负变量$f_{ij}$给出单个商品在边$arc(i,j)$上的流量。仅针对通过分支切割算法求解的对称公式提供了计算结果。这种方法的结果后来由 Hernández-Pérez 和 Salazar-González [16]改进，增强的分支切割算法再次在对称公式上工作，但仅利用二进​​制变量$x_{ij}$。为了解决更大的实例，Hernández-Pérez 和 Salazar-González [17]提出了两种简单的启发式算法，而 Hernández-Pérez 等人引入了性能良好的可变邻域下降元启发式算法variable neighborhood descent metaheuristic。[18] . 所有这些工作都考虑了车辆可以带着一些负载离开站点的情况，但所有请求的总和等于零。⭐️非常好的基础

1-PDTSP 也引起了其他研究人员的兴趣。王等。[19]研究了涉及单位负载请求的 1-PDTSP 的一些变体。他们针对路径上的分布情况以及$Q=1$ 或$Q=+\infty$ 的树上的分布情况开发了多项式时间精确算法polynomial-time exact algorithms. 马丁诺维奇等。[20]提出了一种模拟退火方法simulated annealing approach，而 Zhao 等人。[21]开发了一种遗传算法genetic algorithm。这两种元启发式算法的结果后来由 Hosny 和 Mumford [22]通过可变邻域搜索Variable Neighborhood Search(VNS) 进行了改进，但以非常高的计算时间为代价。Mladenović 等人提出了一种更新的 VNS。[23]使用二叉树有效地执行可行性检查并获得了非常好的计算结果。

• 多项式精确算法
• 启发式算法：
  模拟退火
  遗传算法
  可变邻域算法
• 二叉树

Shi 等人正式介绍了多车辆案例，称为单一商品取货和送货车辆路径问题(1-PDVRP)。[24]，他研究了对每条路线施加最大持续时间限制的情况。他们提出了一个遗传算法和一个使用二元变量$x_{ijk}$的三指数数学公式，如果车辆$k$沿边或$arc(i,j)$ 行驶则取值 1 ，否则取 0，非负变量$f_{ij}$表示单个商品在边$arc(i,j)$. 仅针对在一组随机生成的具有对称成本的实例上测试的遗传算法进行了计算实验。

BRP 是 1-PDTSP 的概括，涉及不止一种车辆。实际上，在接下来的部分中，我们将使用[15]、[16]中适用于 BRP 的成功属性和算法思想。此外，BRP 可以看作是 1-PDVRP 的特例，因为它没有考虑最大路由持续时间。

如前所述，近年来，重新平衡自行车共享系统的问题引起了许多研究人员的兴趣。Benchimol 等人。[25]研究重新分配由单个有能力的车辆执行的情况，允许拆分交付 split deliveries（即，可以多次访问一个顶点）并且所有请求的总和平衡为零。它们提供复杂性结果、下界技术和近似算法，但不提供计算结果。

在最近的一篇论文中，Chemla 等人。[26]再次关注单一车辆案例，允许分批交付。具有空需求的顶点不会被强制访问，但可以被车辆用作在其他站点之间运输自行车时的临时缓冲区。在他们的论文中，作者通过解决对顶点可以访问的最大次数施加限制的问题的松弛来获得下界。他们还通过使用禁忌搜索算法获得上限，并在通过修改[15]中随机创建的实例获得的实例上运行他们的边界程序。

在最近的另一篇论文中，Raviv 等人。[27]定义了静态自行车重新定位问题，其中他们不仅最小化了异构车辆车队的总旅行成本，而且还与每个站点的库存水平的凸函数相关联的用户不满。作者提出了两个 MILP 公式，一个是弧索引的，一个是时间索引的，每个公式代表问题的不同版本。它们允许有限或无限制的拆分交付、有限或无限制的转运、停留在每条路线的最长持续时间和同步转运。本文还介绍了用于加快求解公式的计算时间的精确和启发式方法。

孔塔多等人。[28]提出了自行车重新平衡问题的动态版本的公式，允许使用多辆车。他们的目标函数是服务需求的最大化。提出了一种在离散时间范围内工作的弧流公式，并使用 Dantzig–Wolfe 和 Benders 分解求解。对几个随机创建的实例进行了广泛的测试。

4 . BRP 的 MILP 公式

在本节中，我们介绍了BRP 的四种混合整数线性规划Mixed Integer Linear Programming(MILP) 公式。从初步实验中获得的计算证据向我们表明，最好为 BRP 采用双指数公式。

4.1. Formulation F1

上述双指数公式的起点是众所周知的多旅行商问题Multiple Traveling Salesman Problem( m -TSP)，例如参见 Bektas [29]，其中最多$m$ 辆基于中央仓库的无人驾驶车辆必须访问一个一组顶点，每个顶点只被访问一次的约束。通过定义二进制变量$x_{ij}$ ，如果车辆使用$arc(i,j)$则取值 1 ，否则取 0， m -TSP 可以建模为

目标函数（1）最小化旅行成本。约束(2)和(3)强加了除仓库之外的每个节点都被恰好访问一次。约束条件(4)和(5)分别确保最多m辆车离开站点，并且所有使用的车辆在其路线的尽头返回站点。约束(6)是经典的subtour 消除约束，参见，例如，Gutin 和 Punnen [30], 强加了解决方案的连通性。这些约束呈指数增长，因此，像往常一样，我们以分支切割的方式进行，通过调用分离过程来识别违反的约束和未违反的约束，然后在迭代中仅将违反的约束添加到模型中方式。详情将在下一节中介绍。

为了保证关于 BRP 的解决方案的可行性，我们需要在m -TSP 公式中包含额外的约束，以确保满足需求并且不超过车辆容量。这可以以不同的方式完成。

第一个选项是定义一个额外的连续变量${\theta }_j$ ，表示车辆访问节点$j$后的负载，对于$j\in V$. 考虑到如果车辆沿$arc(i,j)$ 行驶，则${\theta }_j$应等于${\theta }_i+q_j$. 上述限制可以由非线性约束施加：

4.2. Formulation F2

4.3. Formulation F3

4.4. Formulation F4

约束(17)、(18)、(19)、(20)、(29)等同于针对公式 F1 讨论的约束，但适用于新的顶点和弧集。约束条件(22)表明，如果车辆沿弧线 ( i , j ) 行驶，则该弧线上的负载和剩余空间之和等于车辆容量。约束(23)强加了进入和离开顶点的负载和剩余容量之间的差异是该顶点需求的两倍。

离开初始站的总负荷在任何情况下都应该是非负的，而且，如果Q tot取负值，它应该不低于这个值。这一事实是由约束(24)强加的。类似地，约束条件(25)表明进入最终站点的总负载在任何情况下都是非负的，并且在为正的情况下不低于所有需求的总和。不等式(26)表明离开车辆段的车辆的自由空间必须不大于m辆车辆的总容量与总容量加上Q tot之间的最小值。最后，约束(27) , (28)对连续变量强制下限和上限。

5. Branch-and-cut algorithm 分支切割算法

上一节中介绍的模型包含指数数量的约束，因此我们使用分支切割(B&C) 算法来解决它们。我们使用 CPLEX 12.2 的 B&C 框架，它在枚举树的每个节点处求解 MILP 模型的线性松弛，然后调用用户开发的分离程序来添加可能的切割。

在第 5.1 节中，我们提出了一些有效的不等式，我们使用这些不等式将算法的收敛性提高到最优，而在第5.2 节中，我们讨论了我们实现的分离程序。由于不等式和分离程序仅基于x ij变量，因此它们直接适用于公式 1-3。对公式 4 的适应是微不足道的，并在第 5.2 节中进行了概述。

5.1. Valid inequalities 有效的不等式

5.2. Separation procedures 分离程序

本节的目的是介绍我们用来确定我们在第 5.1 节中提出的有效不等式是否被给定解决方案违反的程序$\bar{x}$（可能是分数）。

分离S1和 S2Separations S1 and S2：通过枚举所有可能的顶点i和j对，计算集合S ij，然后评估涉及的不平等超过一个。在下文中，我们将(30)、(31)的分离分别称为分离S1和分离S2 separation S1 and separation S2,。

6 . 基准实例

在我们解决真实世界实例的尝试中，我们从 22 个规模各异的自行车共享系统的网站收集了真实数据。我们研究的城市包括：意大利的巴里、布雷西亚、贝加莫、拉斯佩齐亚、帕尔马、罗马、都灵、特雷维索和雷焦艾米利亚；爱尔兰都柏林；美国的波士顿、丹佛、麦迪逊、迈阿密、明尼阿波利斯和圣安东尼奥；加拿大渥太华和多伦多；墨西哥的墨西哥城和瓜达拉哈拉；阿根廷的布宜诺斯艾利斯和巴西的里约热内卢。

我们已经与这些城市的共享单车运营商取得联系，特别是那些负责自行车重新定位的人员，以获取有关站点位置、理想占用水平、可用车队特征和类型的信息执行的重新定位。并非所有这些都向我们提供了所有必需的信息。一般来说，我们可以说他们中的一些人在夜间进行重新定位，而另一些人也在白天进行。我们从网站上收集了车站和车站的坐标。如果没有可用的车站信息，我们假设车站与其中一个车站位于同一地点。我们使用地理信息系统来计算最短行驶距离$c_{ij}$（以米为单位）每对点之间，考虑两个可能的方向。然后，我们拍摄了每个站点夜间占用水平的快照，并将站点的需求固定为遇到的占用水平与站点所需占用水平之间的差异。事实上，根据大多数运营商提供的信息，最常见的重新平衡站点的规则是每个站点填充一半的插槽，因此我们将站点的期望占用水平设置为其插槽数量的一半. 另请注意，对于那些将站点分配给自行车站的城市，我们将该站的需求设置为 0。

根据我们收集的数据，实践中遇到的最常见的车辆容量是每辆车30辆、20辆和10辆自行车。我们将这三个值应用于为每个城市获得的数据。在某些情况下，使用的最小车辆容量设置为 max ⁡ i ∈ V { ∣ q i ∣ } \max_{i\in V} \{|q_i|\} maxi∈V​{∣qi​∣}，当后者的数量超过 10 时。对于最大需求为 20 的布宜诺斯艾利斯，我们只测试了 20 和 30。我们总共生成了 65 个实例，总结在表 2中。值 min ⁡ { q i } ， a v q { q i } , max ⁡ { q i } , 和 d e v { q i } \min \{q_i\}，avq\{q_i\},\max\{q_i\}, 和dev\{q_i\} min{qi​}，avq{qi​},max{qi​},和dev{qi​}, 是分别给出最小、平均和最大需求，以及标准偏差。为距离$c_{ij}$提供了类似的信息。顶点数从 13 到 116 个站不等。所有测试实例都在离开停车场的自行车数量上有变化（因为平均不为 0）。所有距离均以米为单位。所有实例都可以在http://www.or.unimore.it/resources.htm在线获得。网址似乎打不开了

7 . 计算结果

BRP 的 4 MILP 公式、5 分支裁剪算法中描述的所有算法均使用 C/C++ 编码，并在 Intel Core i3-2100 CPU、3.10 GHz、4.00 GB 上运行。我们使用 CPLEX 12.2 作为 MILP 求解器，强制选择单个处理器。公式 F1–F4 在第 6 节中描述的问题实例上进行了计算测试。为清楚起见，表 3中给出了我们测试的配方的计算实施细节，其中我们还包括第 5.2 节中描述的额外分离程序。

在本节中，我们将介绍使用公式 F1–F4 的 B&C 算法的计算结果。B&C 算法在找到最佳解决方案或经过预定时限时终止。施加的时间限制是 3600 CPU 秒。表 4报告了完整的 65 个问题实例集的计算结果。在此表中，为每个问题实例提供了以下信息：

• city$(|V|,Q)$:与给定问题实例关联的城市名称，由顶点数唯一标识|V|相应有向图的数量和用于在指定城市运输自行车的车辆容量Q。
• UB：B&C 算法使用公式 F1–F4 找到的最佳可行解的值
• $Ga{p}_1-Ga{p}_4$：与UB的百分比偏差$L{B}_1-L{B}_4$，B&C 算法使用核心配方 F1–F4 获得的最佳下限，分别包括每个配方的附加分离集，如表 3所示。$Ga{p}_i=100/(1-L{B}_i/UB)，fori=1,\cdots ,4$.
• Time：运行 B&C 算法的计算时间，以 CPU 秒为单位。

为了比较公式 F1-F4 在整个问题实例上的平均性能，表 4中给出了以下附加信息：

• opt:在 3600 s 内 B&C 算法最优解的问题实例总数 。
• $\#nodes$:：B&C 算法探索的平均节点数（在所有实例中）。
• $\#Cuts$:B&C算法生成的平均切割数。

如表 4所示，前 25 个问题实例和大量其他实例可以在几秒钟内通过所有公式轻松解决。公式 F1 在平均差距、计算时间和生成的切割数量方面给出了最差的结果，而公式 F2 和 F4 在所有性能指标上都表现出相似的性能。另一方面，F3 在平均水平的所有配方中表现最佳$Ga{p}_3=2.24$它以最佳方式解决了所有问题实例，包括最多 50 个顶点。实际上，公式 F3 在平均 15 分钟的时间内为 65 个实例中的 49 个找到了最优解， 平均生成大约 1200 个 B&C 节点。然而，值得注意的是，对于一些较大的实例，Gap 3大于Gap 2（例如，Ciudad de Mexico (90, 17)）或Gap 4（例如，迈阿密 (82, 10)）。通过计算评估每个分离过程对在 B&C 树的根节点计算的最困难问题实例的结果百分比差距的影响，进一步了解了最佳表现公式 F3。

在表 5中，我们测试了核心配方 F3（参见表3），以及通过一次仅包含一个分离程序获得的配方。我们用$Ga{p}_{core}$表示核心版本获得的下限与UB的百分比偏差，而我们使用$Ga{p}^{+}(S_x)$表示核心版本加上分离 $S_x$的结果。

在表 6中，我们展示了配方 F3 的完整版本（即核心配方加上所有分离程序）的结果，以及通过一次从中去除一个分离程序而获得的结果。我们用$Ga{p}_{full}$表示从完整版本获得的下限与UB的百分比偏差，而我们使用$Ga{p}^{-}(S_x)$表示完整版本减去分离 $S_x$的结果。

表 5中报告的结果表明，核心配方 F3 的平均差距接近 7%，但在最坏的情况下略大于 25%——墨西哥城 (90, 20)。通过单独添加分离 S1、S2 或 S5，平均间隙$Ga{p}_{core}$仅略有改善；然而，值得注意的是，分离 S1、S2 和 S5 的计算速度非常快。从表 6中显示的结果可以明显看出分离 S3 以及更清楚地 S4 的重要性，即从完整配方 F3 中去除 S3 和 S4 导致与平均值的百分比差距分别增加$Ga{p}_{full}=7.53$到$Ga{p}^{-}(S3)=8.18$Gap^-(S4)$ 。值得注意的是，对于明尼阿波利斯 (116, 10) 的分离 S4，这一差距从 18.52% 增加到 36.39%。

基于本节中呈现的总体计算结果，我们注意到实例的计算难度不仅像预期的那样随着顶点数量的增加而增加，而且随着车辆容量的减少而增加。Hernández-Pérez 和 Salazar-González [15]也注意到了 1-PDTSP 的这种行为，这是由于小容量车辆被迫执行长而复杂的取货和送货路线。图 4给出了一个说明性示例，它描述了针对以下情况在 Reggio Emilia 出现的问题实例获得的三个最优解：
(i): Q =10，需要3条车辆路线。第一辆车访问了 2、6、13、5、8 和 7 站，第二辆车访问了 1、3、10、4、9 和 11 站，但第三辆车仅访问了 12 号站。总行驶距离为 32.5 公里.
(II):Q =20，需要两条车路。第一个访问站点 13、2、10、4、6、3、1、5、8 和 7，而第二个车辆访问站点 9、11 和 12。总行驶距离为 23.2 公里。
(III):Q =30，单条车路按7、5、8、13、2、10、4、6、3、1、11、9、12的顺序访问所有站点（行驶16.9公里）。

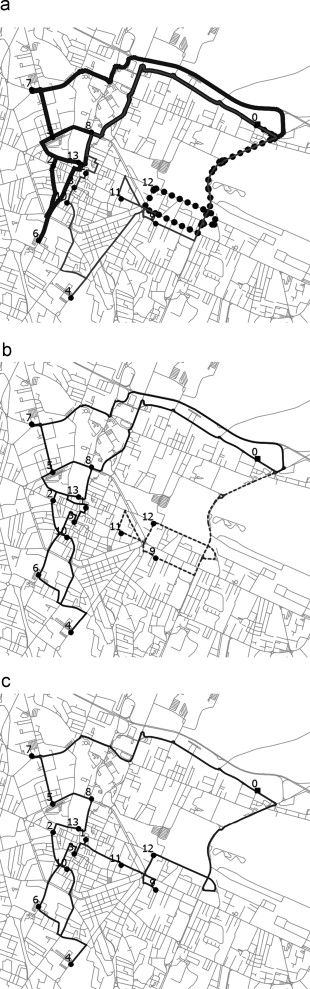
图 4。Reggio Emilia 的最优解 (a) Q =10，(b) Q =20，© Q =30。

7.1. Randomly generated instances 随机生成的实例

结果证实了从解决现实世界实例中获得的计算经验。当增加顶点数量和车辆容量时，实例变得更难解决。具有更好结果的配方再次是 F3。如表 7所示，15 个实例中有 12 个被 F3 求解到最优，最佳上限和最佳下限之间的百分比差距平均低于 0.20%。平均求解时间小于 15 分钟。总的来说，对随机生成实例的测试证实了所提出的算法和公式的质量。

8 . 结论和未来的研究方向

在本文中，我们考虑了自行车重新平衡问题，该问题要求使用一队有能力的车辆以最低成本重新定位自行车共享计划的公共自行车。我们对问题进行了建模，提出了四种不同的公式，其中考虑了不同类型的变量和约束。所有公式都涉及指数数量的约束，因此我们使用分支切割算法解决了它们。

通过从几个网站收集数据，我们制作了一个包含 65 个实例的有趣测试台。我们公开了测试台，并用它来计算评估分支切割算法。计算证据表明最好的计算结果是由配方 F3 产生的。该公式有效地解决了最多 50 个顶点的实例，但可能无法 在标准 PC 上用 1 小时的计算时间解决一些更大的问题。一个有趣的未来研究方向是尝试通过启发式和元启发式算法来解决这些实例。

表2

表4

表5

表6

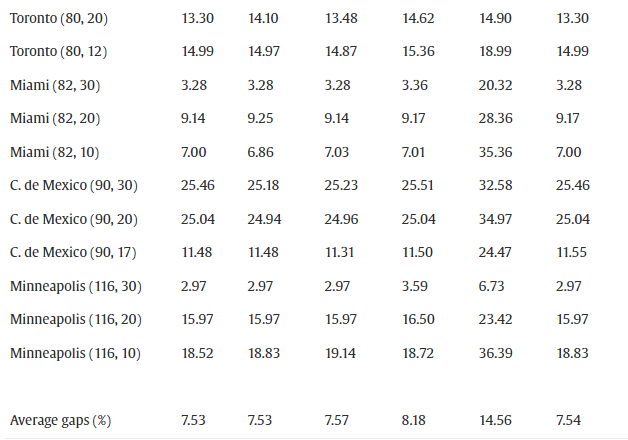
表7