[未]An exact algorithm for the static rebalancing problem arising in bicycle sharing systems

《An exact algorithm for the static rebalancing problem arising in bicycle sharing systems》

@article{SBRP2015,
author = {Erdoğan, G{\"{u}}neş and Battarra, Maria and {Wolfler Calvo}, Roberto},
doi = {https://doi.org/10.1016/j.ejor.2015.03.043},
issn = {0377-2217},
journal = {European Journal of Operational Research},
keywords = { Branch-and-cut, Multiple visits, Pickup and delivery,Bicycle sharing systems},
number = {3},
pages = {667--679},
title = {{An exact algorithm for the static rebalancing problem arising in bicycle sharing systems}},
url = {https://www.sciencedirect.com/science/article/pii/S0377221715002659},
volume = {245},
year = {2015}
}

亮点

突出
•研究了自行车共享系统中出现的路线优化问题。（有桩的）
•提出了该问题的第一个精确算法。
•基础公式是使用从一般整数到二进制变量的变量转换开发的。
•该算法是一种分支和切割算法，它使用组合弯曲者切割。
•最多具有 60 个站点的实例将得到最佳求解。

摘要

自行车共享系统可以显着减少交通、污染和市中心对停车位的需求。自行车共享系统成功的关键之一是再平衡操作的效率，其中每个站点的自行车数量必须由卡车通过提货和送货操作恢复到其目标值(the number of bicycles in each station has to be restored to its target value by a truck through pickup and delivery operations)。静态自行车再平衡问题旨在确定单个车辆要访问的站点的最小成本序列以及每个站点要收集或交付的自行车数量。允许多次访问一个车站，以及将车站用作临时存储。本文从文献中提出了针对基准实例上的问题和计算测试结果的精确算法。计算实验表明，最多 60 个站点的实例可以在 2 小时的计算时间内求解到最优。

一、引言

由于城市中心的公民和服务急剧增加和聚集，城市交通是大城市的一个关键问题。拥塞是一个频繁且主要的问题，相关的决策问题非常复杂。自布坎南报告（布坎南，1963年）以来，土木工程师提出了许多有效的技术来减轻城市化对交通的影响。共享移动系统提供了最有前途的解决方案之一，并有可能减少城市地区的拥堵。特别是，自行车共享系统被证明是解决“最后一英里”问题的有效解决方案（Liu，Jia，&Cheng，2012《Solving the last mile problem: Ensure the success of public bicycle system in Beijing》）。

De Maio（2009）调查了从1960年代开始的自行车共享系统的发展，当时Witte Fiesten（白色自行车）首次在阿姆斯特丹推出。虽然第一代共享单车没有被证明是成功的，但由于更强大和专用的自行车和基于硬币的支付系统，1990年代初在丹麦推出的第二代自行车更有效。第三代于1996年在英国朴茨茅斯大学首次推出，学生可以使用智能卡租用自行车。这一代自行车被证明是成功的，大大减少了盗窃和损坏自行车的数量。人们很快就发现，能够跟踪自行车、存储有关其使用情况的信息以及有关用户的数据的 IT 工具对于提高服务质量和降低自行车被盗/损坏率是必要的。De Maio（2009）报告说，截至2009年，大约有120个自行车共享系统在运行，其中一些由数万辆自行车组成。在增加自行车使用量、减少一氧化碳方面取得了令人印象深刻的成果2还报告了气体排放以及随之而来的公共卫生改善。共享单车系统的效率很大程度上取决于网络运营商实施的运营策略的有效性。

De Maio（2009）确定的第四代自行车共享系统的关键要求之一是良好的再分配系统。尽管采取了旨在促进用户重新分发自行车的举措，但将自行车从高供应/低需求地区转移到低供应/高需求的地区最常用的技术是使用卡车。使用大型卡车可能很昂贵并且具有沉重的一氧化碳2因此，许多城市转向电动汽车或开始使用车辆路线优化软件来降低运输成本和燃料消耗。

在本文中，我们研究了由Benchimol，Benchimol，Chappert，De La Taille，Laroche，Meunier和Robinet（2011）引入的静态自行车再平衡问题（SBRP）。SBRP旨在为在仓库开始和结束服务的车辆找到一条最低成本路线，并通过根据需要拾取和交付自行车，将每个自行车站的库存水平恢复到目标值(The SBRP aims to find a minimum cost route for a vehicle that starts and ends its service at a depot, and restores the inventory level at every bicycle station to its target value by picking up and delivering bicycles as necessary)。车辆可以多次访问任何站点，并且可以将站点用作自行车的临时存储（即抢占）(The vehicle may visit any station more than once, and may use stations as temporary storage for bicycles (i.e., preemption))。术语静态是指假设每个站点的自行车数量是事先知道的，并且在取货和交付操作期间不会改变，而不是动态问题，其中由于用户租用和归还自行车，自行车数量在操作期间可能会发生变化。SBRP对许多在夜间重新平衡车站的自行车共享系统感兴趣。尽管Chemla，Meunier和Wolfler Calvo（2013）已经研究了SBRP，但作者成功地提供了强大的下限和有效的启发式解决方案方法，但不是精确的算法。在这项研究中，我们提出了一种精确的SBRP算法，并从文献中对基准实例提出了广泛的计算结果。

本文的其余部分组织如下。在第2节中，我们提供了有关自行车共享系统中出现的自行车再平衡问题的文献综述。在第 3 节中，我们介绍了 SBRP 的数学问题定义。在第 4 节中，陈述了 SBRP 的确切算法的元素。在第 5 节中，我们提出了一个简单的启发式方法来生成上限。在第 6 节中，我们提供了计算实验的结果。最后，我们在第7节中作结论性发言。

2. Literature survey

人们对自行车共享系统中出现的优化问题越来越感兴趣。研究的问题包括自行车共享系统与其他交通系统的集成（Chow&Sayarshad，2014），在单向车辆共享系统中保留停车位的问题（Kaspi，Raviv和Tzur，2014），白天自行车使用的动态（Agatz，Erera，Savelsbergh，&Wang，2011），以及燃料价格变化对自行车使用的影响（史密斯和考尔曼，2011）。最近，自行车再平衡问题引起了研究界的极大兴趣。鉴于高度的复杂性，已经提出了元启发式来解决更大的实例和多个车辆的问题。我们向感兴趣的读者推荐Rainer-Harbach，Papazek，Raidl，Hu和Kloimüllner（2014），Papazek，Raidl，Rainer-Harbach和Hu（2013），Gaspero，Rendl和Uli（2013）以及Schuijbroek，Hampshire和van Hoeve （2013）的启发式论文。 在下文中，我们将重点研究自行车再平衡问题的确切方法。

Nair和Miller-Hooks（2011）通过使用随机规划研究重新平衡共享移动系统的动态问题，其中每个站点的需求使用一组场景进行建模。他们的建模方法使用机会约束，这保证了重新分发计划将满足给定百分比的方案。目标是尽量减少重新分发成本。但是，此模型不返回任何操作路由决策。Contardo，Morency和Rousseau（2012）使用在时空网络上定义的流公式解决了动态再平衡问题，旨在最小化整体未满足的需求。该公式通过嵌入在列生成框架中的 Benders 分解来解决。我们推荐感兴趣的读者阅读Chemla，Meunier，Pradeau，Wolfler Calvo和Yahiaoui （2013）以进一步阅读动态问题。

Raviv，Tzur和Forma（2013）研究了多车辆静态再平衡问题，其目标是同时最小化路线成本和客户不满。后者使用车站自行车数量的分段线性凸函数进行建模。当车站已满（客户将无法归还自行车）或空（客户将无法租用自行车）时，车站的客户不满意功能达到最大值。假设最多访问一次车站，考虑服务时间，并且每辆车的总行程时间是有限的。作者提出了两种数学公式，优势规则和有效不等式。它们的配方在多达 60 个站点和一两辆车的人工实例上进行测试。作者还介绍了受华盛顿特区首都共享单车启发的实例，该实例最多有 104 个车站。这两种公式都难以解决两辆车相对于一辆车的情况。此外，作者指出，单次访问的限制是限制性的，可能会大大限制所实现的解决方案的质量。

Chemla，Meunier和Wolfler Calvo（2013）提出了一个在时间扩展图上定义的SBRP的数学公式，其中每个站点被复制的次数与对该站点的可能访问次数的上限一样多。该公式使用四个指数变量，对于中型 SBRP 实例来说变得棘手。因此，作者引入了两个松弛，第一个放宽使用两组双索引变量，分别对应于每个弧的遍历次数和每个弧上携带的自行车数量。第二个松弛仅使用表示弧遍历次数的变量。事实证明，这两种松弛是等效的，但由于更强的容量约束，第二个松弛的线性松弛提供了更高质量的下限。还开发了禁忌搜索算法，并生成了一组基准实例，最多可访问100个站点。作者报告说，目前容量为 Q = 20 辆自行车的车辆在巴黎访问的车站数量通常为 50 辆，每个车站可容纳 30 辆自行车。对于实际大小的实例，最佳上限解决方案和下限之间的差距约为 2%，对于最多具有 5 个站点的实例，差距最高为 100%。

Erdoǧan， Laporte， and Wolfler Calvo （2014） 通过假设重新定位后车站的自行车数量应该在给定的时间间隔内而不是特定的目标数量，并且最多可以访问一次车站，从而扩展了单车静态再平衡问题。作者使用两种方法精确地解决了这个问题，一种是基于Benders分解的分支和切割算法(a Benders decomposition based branch-and-cut algorithm)，另一种是传统的分支和切割算法(a traditional branch-and-cut algorithm)。利用该问题与一个商品取货和送货旅行推销员问题(One Commodity Pickup and Delivery Traveling Salesman Problem )（1-PDTSP）的相似性，他们采用了Hernández-Pérez，Salazar-González，2004年，Hernández-Pérez，Salazar-González，2007年深入研究的有效不等式。 具有多达 50 个站点的实例已被求解到最佳状态，并且观察到基于 Benders 分解的分支和切割算法优于传统的分支和切割算法。

Dell’Amico，Hadjicostantinou，Iori和Novellani（2014）解决了多车辆静态问题，其中整体运输成本最小化，每个车站必须恰好访问一次。比较了四种备选的混合整数线性数学公式，并使用不等式来加强公式。

3. Problem definition

我们现在提供 SBRP 的数学定义。我们得到一个完全的有向图(a complete directed graph) $G=(V，A)$。顶点集 V = { 0 ， 1 , . . . , n } V = \{0， 1,..., n\} V={0，1,...,n}, 由depot（顶点 0，车辆的到达和离开节点）和bicycle station V \ { 0 } V\backslash \{0\} V\{0} 组成。车站 i ∈ { 1 , . . . , n } i ∈ \{1,..., n\} i∈{1,...,n} 的自行车数量最初为$p_i$，自行车的目标数量为$q_i$，而 $i$站的容量为$C_i$.请注意，容量是必需的，因为允许抢占。因此，最初平衡的station（即$p_i=q_i$）也可以以临时停车或收集自行车为目的进行访问。每个弧 $(i，j)$都有相关的行程成本$c_{ij}$，可能表示油耗、行驶时间或 CO2排放。车辆一次最多可以携带Q自行车。目标是最大限度地降低整体解决方案成本，确保车辆出发并到达仓库，并在旅行结束时将目标数量的自行车分配给每个站点。

SBRP已被证明是$\mathcal{NP}-hard$ by Benchimol et al. (2011)(Balancing the stations of a self-service bike hire system)，以及其完整图和单位成本二分图的特殊情况。作者还提出了一种针对一般情况的 9.5 近似算法，一种用于具有完整图形和单位成本的特殊情况的 2 近似算法，以及下界技术。Chemla，Meunier和Wolfler Calvo（2013)(Bike sharing systems: Solving the static rebalancing problem)证明，验证在SBRP实例的仓库开始和结束的顶点序列是否代表可行的解决方案的问题是一个搜索问题（即，多项式时间算法能够为每个行进的弧找到车辆上自行车的可行分配， 如果存在任何可行的分配）【the problem of verifying if a sequence of vertices starting and ending at the depot for an instance of SBRP represents a feasible solution is a search problem (i.e., a polynomial time algorithm is capable of finding a feasible assignment of bicycles on the vehicle for each arc traveled, if any feasible assignment exists)】。另一方面，如果唯一可用于表示解决方案的信息是网络中每个弧被遍历的次数，则确定此信息是否对应于可行解决方案的问题为$\mathcal{NP}-complete$

NP-hard与NP-complete可以查看资料：
《算法时间复杂度及P、NP、NP-Complete、NP-Hard问题》
《怎么理解 P 问题和 NP 问题？》
《如何证明一个问题是NP-Hard或NP-Complete?》

我们现在提出了Chemla，Meunier和Wolfler Calvo（2013）对SBRP第二次放宽的简化版本，它将作为完整配方的垫脚石。作者将站$i\in V$ 的不平衡定义为$d_i=p_i-q_i$，站点的子集 S ∪ V \ { 0 } S \cup V\backslash \{0\} S∪V\{0}的净不平衡表示为为 $d(S)={\sum }_{i\in S}{d}_i$，并引入一个函数 $\mu (S)$，如果至少有一个站 $i\in S$ 使得 $|d_i|>0$，否则为 0。根据这些定义，它们对连接和容量使用两组单独的约束。这两组约束可以表示为通过定义和使用单个函数去计算站点集 S ⊆ V \ { 0 } S ⊆ V\backslash \{0\} S⊆V\{0} 的最小车辆要求的单个集合,为

S是一个站点子集，并不知道是否包含不平衡点$|d_i|>0$
$d(S)=\{\begin{array}{ll}1,& S中至少有一个不平衡站点\\ 0,& 都是平衡站点\end{array}$
花括号中第一值，表示车辆装满了的最高次数
$r(S)$：最小的车辆数目
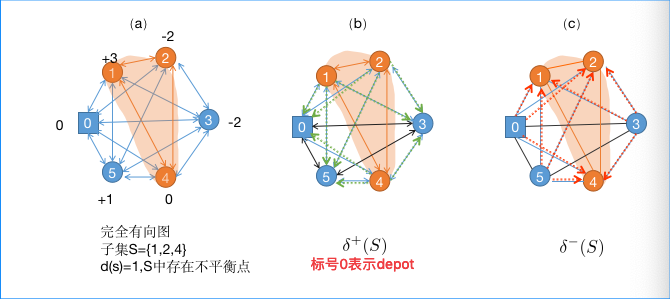
G=（V,A）是一个完整的有向图，所以弧(i,j)和弧(j,i)是不相同的。示意图如下。

• ${\delta }^{+}(S)=\{(i,j)\in A:i\in S，j\notin S\}$ : $(i,j)$是弧集合A中的arc,其中$i$是子集S中的节点，j不是子集S中的节点。
• ${\delta }^{-}(S=\{(i，j)\in A：i\notin S，j\in S\}$: $(i,j)$是弧集合A中的arc,其中$i$是子集S中的节点，j不是子集S中的节点。
  

此外，我们分享了 ${\delta }^{+}(S)=\{(i,j)\in A:i\in S，j\notin S\}$ 和 δ − ( S ） = { （ i ， j ） ∈ A ： i ∉ S ， j ∈ S } δ ^-(S） = \{（i， j） ∈ A： i∉S， j ∈ S\} δ−(S）={（i，j）∈A：i∈/S，j∈S}的定义。令$x_{ij}$等于遍历弧$(i,j)\in A$的次数【 Let xij be equal to the number of times arc (i, j) ∈ A is traversed】。我们写$x(S)$表示为${\sum }_{(i,j)\in S}{x}_{ij}$. Chemla， Meunier， and Wolfler Calvo （2013）《Bike sharing systems: Solving the static rebalancing problem》 证明，两个站之间具有正不平衡值或两个负不平衡值的弧线不需要多次遍历【an arc between two stations with both positive or both negative imbalance values need not be traversed more than once】。当旅行成本受三角不等式约束(the travel costs respect the triangle inequality)时，我们观察到arcs $(i,j)\in A:d_i>0,d_j<0or{d}_i<0,d_j>0$ ,最大遍历次数等于不平衡绝对值的最小值(the maximum number of traversals is equal to the minimum of the absolute values of the imbalances)（即，每次通过时至少运送一辆自行车）。因此，我们将弧可以遍历的最大次数表示为

举例说明：弧可以遍历的最大次数$u_{ij}$,

• (1,2): 节点1为+3，节点2为-2，$min(|+3|,|-2|)=2$
• (1,5):节点1为+3，节点5为+1，遍历次数为1
• (1,4):节点1为+3，节点4为0，遍历次数为1

• (3): $x_{ij}$是遍历有向弧(i,j)的次数，$c_{ij}$是弧(i,j)的成本。–>将总的旅行成本将至最低。
• (4):${\delta }^{-}(i)$是流向节点i的弧集合，$x({\delta }^{-}(i))$是节点i的入流量。–>流量守恒约束。
• (5):${\delta }^{+}(0)$是流出depot的弧集合，$x({\delta }^{+}(0))$是驶出depot的数量。$d_0$是仓库包含的数量，Q是vehicle的最大容量，$\lceil |d_0|\rceil /Q$是需要几趟车的数目。–>驶出depot的最小行程数量。
• (6): S是一个站点集合的子集，$r(S)$是集合S需要的vehicle的数目，$x({\delta }^{+}(S))$是离开集合S的流量。–> 规定了离开集合S的流量的下线。
• (7)变量的取值范围。

（SBRP-R）有两个缺点，使它无法成为一个完整的配方。🐸首先，如上一节所述，证明（SBRP-R）的integral solution(整数解？积分解？)是可行的,因为SBRP是一个NP完全决策问题(an integral solution for (SBRP-R) is feasible for the SBRP is an NP-complete decision problem)。🐸其次，没有直接的方法来分离integral solution,它被认为对于SBRP是不可行的。为了观察这一点，假设我们有这样的解决方案 $x^{\ast }$。若要分离此解决方案，应将以下约束添加到约束集中。

where y i j k ∈ { 0 , 1 } , ∀ ( i , j ) ∈ A , k ∈ { 0 , ⋯   , ⌊ log ⁡ 2 ( u i j ⌋ ) y_{ijk}\in \{0,1\},\forall (i,j) \in A,k\in \{0,\cdots,\lfloor \log_2(u_{ij}\rfloor) yijk​∈{0,1},∀(i,j)∈A,k∈{0,⋯,⌊log2​(uij​⌋). 注意到$u_{ij}:{\log }_2(u_{ij})=\lfloor {\log }_2(u_{ij}\rfloor$,转换允许${\sum }_{k=0}^{\lfloor {\log }_2(u_{ij}\rfloor }{2}^k{y}_{ijk}>u_{ij}$,但提供$u_{ij}$上限是为了加快算法而不是可行性。

• $x_{ij}$表示遍历弧(i,j)的次数。
• (8)的左侧表示 A中任意弧上的两个 遍历次数 差值总和，要求大于1。表明解x与$x^{\ast }$是不同的。
• 对于二进制变量，可以通过下面方法线性化它

$|x_{ij}-x_{ij}^{\ast }|=\{\begin{array}{ll}{x}_{ij},& x_{ij}^{\ast }=0\\ 1-x_{ij},& x_{ij}^{\ast }=1\end{array}$

• x i j ∈ { 0 , 1 , 2 , ⋯   , u i j } x_{ij}\in \{0,1,2, \cdots,u_{ij}\} xij​∈{0,1,2,⋯,uij​},$u_{ij}$弧可以遍历的最大次数(根据定义式计算得来的)
• 由于一般的整数变量$x_{ij}$没有有效办法进行线性化，因此使用了公式(9)的转化整数变量。

给定一个整数解$y^{\ast }$, 让我们定义$I_0(y^{\ast })=\{(i,jk):y_{ijk}^{\ast }=0\}$,即变量(们)的索引集等于0.类似的，我们可以定义$I_1(y^{\ast })=\{(i,jk):y_{ijk}^{\ast }=1\}$，即变量(们)的索引集等于1.最后，我们定义不可行的指示函数$I_f(y^{\ast })$,如果$y^{\ast }$是一个整数解对于SBRP是不可行的，则返回1；否则，返回0.基于这些定义，可以用组合Benders’cut分离出对SBRP不可行的整数解（Codato & Fischetti，2006）。

公式(8)可以转化为公式(10),其中的一般整数变量$x_{ij}$可以根据公式(9)变化；(8)中的绝对值也可以去掉了(根据$x^{\ast }$是一个二进制变量)

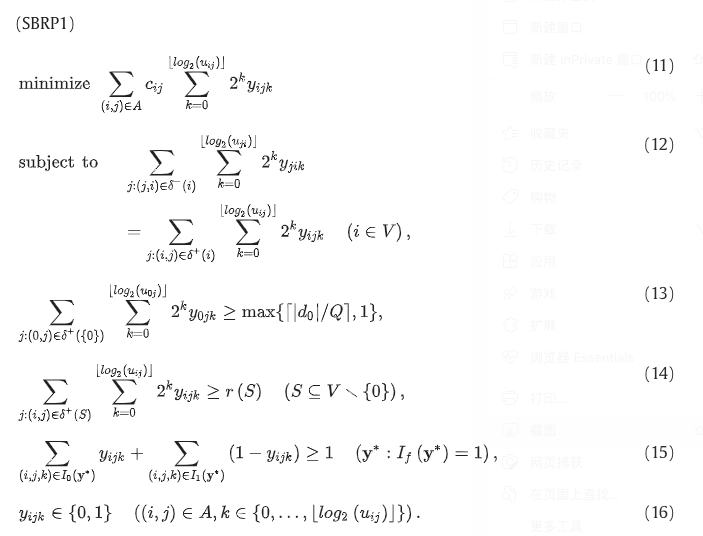
同理，我们将(SBRP_R)中的一般变量改为二进制变量。

与 SBRP-R 一样，目标函数 （11） 最小化总行驶成本，约束集 （12） 是流量守恒约束，约束集 （13） 表示离开车辆段的最小行程次数，约束集 （14） 规定了车辆必须离开 S 的次数下限。约束集 （15） 分隔对 SBRP 不可行的整数可行解。最后，（16）声明所有变量y艾克是二进制的。为了分离约束集（14），我们使用了Hernández-Pérez和Salazar-González （2007）中描述的1-PDTSP分离算法。（15） 的分离算法将在下一节中详细介绍。

4. Separation algorithms

在本节中，我们提供了分离组合弯曲者切割的算法，并提出了分离算法的修改，以允许解决不允许抢占的 SBRP。

4.1. Separation algorithm for combinatorial Benders’ cuts

来自 Chemla、Meunier 和 Wolfler Calvo （1） 基准实例集的测试实例 n20q10C 的 SBRP2013 最优解如图 1 所示，其中从 i ∈ V 到 j ∈ V 的弧数计算为 ${\sum }_{k=0}^{\lfloor {\log }_2(u_{ij}\rfloor }{2}^k{y}_{ijk}$.每个顶点旁边是与顶点对应的初始和目标库存级别。顶点 2、10、12 和 16 的入度数为 2，而其余顶点仅访问一次。如上一节所述，检查此解决方案是否对应于 SBRP 的可行解决方案是一个 NP 完全决策问题。现在，我们提供了一种算法来检查SBRP1的整数可行解对于SBRP的可行性。
图 1.配方SBRP1对实例n20q10C的最佳解。

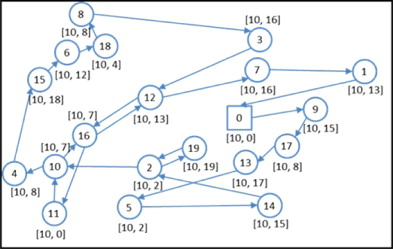
该算法基于两个观察结果。首先，任何穿过公式 SBRP1 解弧的 SBRP 解对应于在仓库开始和结束的欧拉回路，在由xij.其次，在仓库开始和结束的欧拉回路可以表示为时间扩展网络，其中顶点的时间维度由它们的访问顺序定义。SBRP解决方案的可行性可以通过解决该网络上的流量问题来检查。基于这些观察结果，我们可以得出结论，约束集（15）的精确分离算法应该（隐式或显式）枚举SBRP1解的所有欧拉电路，并通过求解相应时间扩展网络上的流问题来检查每个欧拉电路的可行性。如果它包含的至少一个欧拉回路对相应的流动问题具有可行的解，则宣布该解可行。否则，可以通过从约束集 （15） 中添加不等式来分离解。

…未完，以后再补充吧