
@article{BRP2021brokenbikes,
address = {Univ Hong Kong, Dept Civil Engn, Pokfulam Rd, Hong Kong, Peoples R China},
author = {Wang, Yue and Szeto, W Y},
doi = {10.1016/j.trc.2020.102895},
issn = {0968-090X},
journal = {TRANSPORTATION RESEARCH PART C-EMERGING TECHNOLOGIES},
mendeley-groups = {rebike21-23},
title = {{An enhanced artificial bee colony algorithm for the green bike repositioning problem with broken bikes}},
volume = {125},
year = {2021}
}
突出
• This study tackles a static green bike repositioning problem with broken bikes.
本研究解决了自行车断裂的静态绿色自行车重新定位问题。
•We proposed a hybrid heuristic based on the Enhanced Artificial Bee Colony algorithm.
我们提出了一种基于增强人工蜂群算法的混合启发式算法。
• We use the Enhanced Artificial Bee Colony algorithm to generate the vehicle route.
我们使用增强型人工蜂群算法来生成车辆路线。
•We propose a linear program and a heuristic to compute loading quantities at visited stops. 我们提出了一个线性程序和一个启发式方法来计算所访问站点的装载量。
• The proposed hybrid heuristic outperforms two benchmark methods.
所提出的混合启发式方法优于两种基准方法。
摘要
近年来,自行车重新定位问题(Bike Repositioning Problem)(BRP)引起了许多研究人员的关注,以提高自行车共享系统(BSS)的服务质量。它主要是设计车辆在站点之间转移自行车的路线和装载说明,以达到理想的状态。本研究涉及静态绿色BRP,旨在最大限度地减少重新定位车辆的 二氧化碳排放量,同时在时间预算内尽可能多地实现车站的目标库存水平(This study tackles a static green BRP that aims to minimize the CO2 emissions of the repositioning vehicle besides achieving the target inventory level at stations as much as possible within the time budge)。考虑两种类型的自行车,包括可用自行车和破损自行车(usable and broken bikes)。采用增强型人工蜂群(Enhanced Artificial Bee Colony)(EABC)算法生成车辆路线。提出启发式和精确两种方法,并将其纳入EABC算法,以计算每个停靠点的装卸量。在具有 10-300个站点的真实实例 上进行计算实验。结果表明,所提出的基于启发式加载方法的求解方法能够为小型实例提供最优解。对于大规模实例,它可以产生比文献中的两种基准方法更好的可行解决方案。
1. Introduction
在自行车共享系统(Bike Sharing Systems)(BSS)中,人们可以租用共享自行车来满足短途旅行的需求,例如家庭和地铁站之间的连接,或者只是休闲旅行。但是,由于存在不对称的自行车流,一些站点可能会用返回的自行车填充,而其他一些站点则是空的(due to the existence of asymmetric bike flows, some stations may be filled-in with returned bikes while some others are empty.)。例如,在早高峰期间,住宅区的自行车站可能是空的,而商业区的自行车站可能已经满了。在丘陵地区,底部的车站可能已满,而顶部的车站可能是空的,因为下坡旅行通常比上坡旅行更多。因此,自行车需要在一段时间后在所有站点之间重新分配,以便在每个站点保持理想的库存水平,以满足即将到来的用户的需求。此操作问题称为Bike Repositioning Problem自行车重新定位问题 (BRP)。
重新定位操作主要是使用专用的卡车或拖车车队在站点之间运输自行车,以达到每个站点的预期库存水平(Raviv et al., 2013)。通常有两种类型的重新定位:静态和动态。对于当前大多数研究关注的静态重新定位(例如,Cruz et al., 2017, Ho and Szeto, 2017, Liu et al., 2018, Szeto and Shui, 2018),假设每个站点的自行车库存和需求水平随着时间的推移相对稳定。动态重新定位考虑了一天内自行车库存和需求水平随时间的变化(参见Ghosh等人,2017年,Zhang等人,2017年,水人和司徒,2018年,Brinkmann等人,2019年)。这两种类型的重新定位考虑了不同的应用场景。
在大多数BRP研究中,目标主要集中在两个方面:用户相关因素,如未满足的需求或用户不满(user-related factors such as the unmet demand or user dissatisfaction),以及与运营商相关的因素,如运营成本或行驶距离(operator-related factors such as the operating costs or travel distances)。有人指出,许多城市在规划自行车重新定位活动时开始使用优化软件来降低油耗(Erdoğan et al., 2015)。因此,除了满足客户需求外,BSS的运营商,尤其是那些国有运营商,可能还希望尽量减少重新定位造成的排放或油耗。Wang和Szeto,2018,Shui和Szeto,2018分别在静态和动态重新定位问题中捕捉到了这一点。除了排放最小化目标函数外,Wang和Szeto(2018)还考虑了除了在车站之间重新定位可用自行车外,还需要运回车辆段的破损自行车。然而,他们提出的数学模型不能被商业求解器有效地求解。因此,需要一种启发式方法来解决此类问题。
在本文中,我们提出了一种启发式方法来解决Wang和Szeto(2018)引入的破损自行车的静态绿色自行车重新定位问题(green bike repositioning problem)(GBRP),但仅考虑单辆车,时间预算和修改的目标函数。该问题旨在设计重新定位车辆的路线和装载指令,以便将与目标库存水平的绝对偏差、车站自行车损坏造成的罚款以及重新定位车辆的二氧化碳排放量的加权和最小化(The problem aims to design the route and loading instructions for the repositioning vehicle such that the weighted sum of the absolute deviation from the target inventory level, the penalty caused by broken bikes at stations, and the CO2 emissions of the repositioning vehicle are minimized)。车辆从仓库开始,在自行车站之间转移自行车以使库存水平接近目标值,并在时间预算内收集损坏的自行车,然后在仓库结束(The vehicle starts from the depot, transfers bikes among bike stations to bring the inventory level close to the target value, and collects broken bikes before ending at the depot within the time budget)。所有车站和车站都可以多次参观。假设该仓库具有无限的容量和自行车供应。挑战在于确定每次访问中车站和仓库的两种类型自行车的装卸数量,以便将绝对偏差、罚款和排放的加权总和降至最低(The challenge lies in determining the loading/unloading quantities of two types of bikes at a station and the depot in each visit so that the weighted sum of absolute deviations, penalty, and emissions can be minimized)。在这项研究中,我们采用了Szeto等人(2011)提出的增强人工蜂群(EABC)算法作为所提方法的支柱,以求解多达300个站点的大型实例。采用自适应本地搜索来提高求解质量。装载/卸载量通过求解线性规划模型或启发式方法确定。为了证明所提方法的准确性和效率,我们将结果与 CPLEX 在最多 30 个站点的实例上的结果进行了比较。计算实验也使用规范遗传算法和Alvarez-Valdes等人(2016)提出的方法进行。 结果表明,EABC算法在此类问题上优于其他两种算法。
本文的贡献如下:
- We propose a first model for the bike repositioning problem considering the emissions of the repositioning vehicle, broken bikes, and the time budget simultaneously.
我们提出了自行车重新定位问题的第一个模型,同时考虑了重新定位车辆的排放、损坏的自行车和时间预算。 - We develop an EABC algorithm incorporating an adaptive local search procedure to solve the green BRP with broken bikes.
我们开发了一种EABC算法,其中包含自适应本地搜索程序,以解决自行车损坏的绿色BRP。 - We provide two methods to determine the loading/unloading quantities of two types of bikes at a station and the depot in each visit.
我们提供两种方法来确定每次访问中车站和仓库的两种类型自行车的装卸数量。
本文的其余部分组织如下。第 2 节回顾了 BRP 中的目标函数、自行车类型和现有方法。 第 3 节介绍了问题表述。第 4 节提供了 EABC 算法的算法结构。在第5节中,演示了所提出的求解实际实例的方法的性能。最后,第6节结束了本文,并提出了未来的工作。
2. Literature review
在本节中,我们首先回顾BRP中目标函数中考虑的因素。然后,我们研究了考虑损坏自行车或多种类型自行车的研究。之后,我们将讨论解决BRP的现有方法。
如前所述,目前大多数关于BRP的研究都考虑了目标函数中的用户相关因素或/和操作员相关因素。用户相关因素主要关心用户的需求。例如,未满足未来需求的预期数量(Brinkmann等人,2019),不满足自行车或储物柜需求的惩罚成本(Ho和Szeto,2017),预期的用户不满意(Zhang等人,2017),以及与目标库存水平的偏差(Kloimüllner等人,2014,Di Gaspero等人,2016)。运营商相关因素主要反映运营成本,例如总旅行时间(Angeloudis 等人,2014 年,Dell’Amico 等人,2016 年)、路线成本(Cruz 等人,2017 年)、装卸操作(Rainer-Harbach 等人,2015 年,Liu 等人,2018 年)等。总之,在规划重新定位工作时,始终会考虑自行车用户和系统操作员的收益/成本。
BRP 与车辆配送问题密切相关,因为两者都需要确定车辆路线。在车辆路线问题上,许多研究考虑了环境问题,以促进绿色物流(更多例子见Lin等人(2014))。对于BRP来说,除了自行车用户和系统运营商的收益/成本外,重新定位自行车对环境的影响也引起了我们的注意。大多数静态重新定位工作是由化石燃料卡车进行的,因为与自行车拖车或其他重新定位车辆相比,它们的容量更大,续航里程更长(Wang和Szeto,2018)。然而,排放污染物和一氧化碳 可能违背开发BSS的初衷。 现代技术通过提高燃烧效率或净化除二氧化碳以外的废气,可以减少尾气中的有害物质 (Kopfer 等人,2014 年)。其中一些污染物,如CO和CH,在进一步氧化 后被烧成CO2。二氧化碳 是温室气体的主要成分(约26%),导致影响气候和生态系统的温室效应。在BRP中考虑环境问题的研究有限。据我们所知,只有Wang和Szeto,2018,Shui和Szeto,2018在BRP的客观函数 中捕获了CO2的排放成本。
为了在BRP的目标函数 中捕获CO2的排放成本,需要一个CO 2 排放模型。Demir等人(2011)研究了不同的CO 2 排放模型,考虑了三类因素:车辆相关因素,如车辆类型vehicle type,有效载荷payload,发动机engine和燃料 fuel;与环境相关的因素,如路况和天气;和交通状况。实验结果表明,油耗和CO 2 排放量对车速、负载和道路坡度的变化很敏感(fuel consumption and consequently CO2 emissions are sensitive to the change in vehicle speed, load, and road gradient)。对于通常在夜间发生的静态重新定位问题,可以假设车速恒定。此外,道路坡度可以集成到不对称距离矩阵中(Wang和Szeto,2018)。如果忽略微不足道或无法测量的因素,二氧化碳排放量可以表示为行驶距离和车辆负载的函数。Xiao等人(2012)发现油耗率与车辆负载之间存在线性关系。基于这项研究,Zhang等人(2014)将其扩展到CO 2 排放模型如下:
 其中
e
e
e是 CO 2 排放量,
C
E
R
CER
CER是CO 2 排放率,
ρ
0
\rho_0
ρ0和
ρ
∗
\rho^*
ρ∗分别是车辆空载和满载时的油耗率,
Q
Q
Q是车辆容量,
d
d
d 是负载 q 的行驶距离.此功能与 BRP 中的其他差旅成本函数不同,因为它不仅涉及行驶距离,还涉及车辆负载和行驶距离的乘积。这个性质意味着简单的贪婪加载启发式(例如,Rainer-Harbach等人。,2013)可能不起作用,因为在停车时装载太多自行车可能会加剧排放。Wang和Szeto(2018)也表明,较短的距离不一定会导致较低的排放。此外,对于多次访问的情况,每个站点装载到车辆上的自行车数量可能会影响排放,而不会改变行驶距离()0for the multiple-visit case, the number of bikes loaded onto the vehicles at each stop may affect the emissions without changing the travel distance)。因此,在排放最小化目标下处理所访问站点装载指令的策略应与距离最小化目标下的策略不同。
其中
e
e
e是 CO 2 排放量,
C
E
R
CER
CER是CO 2 排放率,
ρ
0
\rho_0
ρ0和
ρ
∗
\rho^*
ρ∗分别是车辆空载和满载时的油耗率,
Q
Q
Q是车辆容量,
d
d
d 是负载 q 的行驶距离.此功能与 BRP 中的其他差旅成本函数不同,因为它不仅涉及行驶距离,还涉及车辆负载和行驶距离的乘积。这个性质意味着简单的贪婪加载启发式(例如,Rainer-Harbach等人。,2013)可能不起作用,因为在停车时装载太多自行车可能会加剧排放。Wang和Szeto(2018)也表明,较短的距离不一定会导致较低的排放。此外,对于多次访问的情况,每个站点装载到车辆上的自行车数量可能会影响排放,而不会改变行驶距离()0for the multiple-visit case, the number of bikes loaded onto the vehicles at each stop may affect the emissions without changing the travel distance)。因此,在排放最小化目标下处理所访问站点装载指令的策略应与距离最小化目标下的策略不同。
据我们所知,除了对Shui和司徒(2018)的研究外,现有的BRP研究都没有提出一种策略来处理考虑到排放最小化目标的访问站点的装载指令(a strategy to deal with the loading instructions at visited stations considering an emission-minimization objective)。但我们的研究在以下方面与他们不同:🐸首先,我们的研究考虑了两种类型的自行车,而 Shui 和 Szeto (2018) 只考虑了可用的自行车;🐸其次,我们的研究允许在一个规划范围内多次访问车辆段和车站,但司徒和水(2018)要求车辆在每个时期最多访问每个节点一次。因此,需要一种在排放最小化目标下处理所访问站点装卸量的方法。
除了上述排放最小化目标函数外,我们还考虑了BSS中的破损自行车。 在BSS中,损坏的自行车几乎是不可避免的,并且意味着用户的不满,因为它们不能用于满足自行车需求,并且额外占用了停车的储物柜(Kaspi等人,2017)。因此,损坏的自行车需要收集并运走进行维修。一份关于西雅图自行车共享的报告显示,在 2019 年第 3 季度,工作状态不佳的自行车比例达到 18.4%(西雅图交通部,2019 年)。这个比例不小,不容忽视。因此,在 BRP 中捕获损坏的自行车非常重要。
很少有研究提出在BRP中考虑破损自行车的方法。 Alvarez-Valdes等人(2016)在他们的研究中考虑了可用和破损的自行车。他们首先解决了最小成本流程问题,并使用插入算法来处理可用的自行车。之后,损坏的自行车入路线。然而,没有考虑弧流对目标函数的影响。Chang等人(2018)在他们的研究中考虑了一个错误的共享单车回收问题,但他们没有同时考虑可用自行车的重新定位。Zhang等人(2018)使用混合离散粒子群优化算法为可用和损坏的自行车解决了BRP问题的整数线性规划模型。装卸数量预先确定为车站的需求/供应。Wang和Szeto(2018)提出了一个MILP来制定一个BRP,其中同时考虑了排放成本目标函数,可用自行车和破损自行车,但如果不采用启发式方法,确切的方法就无法解决大型实例。因此,解决自行车破损的BRP仍在探索中。
除了破损的自行车,BRPs中也考虑了其他类型的自行车。 Li等人(2016)研究了多种类型自行车可用的情况。这些自行车可能有不同的替代和占用策略。例如,单座自行车可以占据两座自行车的车厢,但不能满足双座自行车的需求。相反,双座自行车可以满足单座自行车的需求,但不能使用单座自行车的隔间。他们的研究与我们的研究之间的区别在于,单座和双座自行车都可以使用。贪婪启发式方法可用于计算装载/卸载量,因为目标函数与车辆负载无关。但是,这种方法不能应用于我们的问题。
为了求解BRP,精确的方法可以在合理的时间内为小型BSS提供最优解。例子包括Dantzig-Wolfe分解和Benders分解方法(Contardo等人,2012)以及分支和切割算法(Dell’Amico等人,2014,Erdoğan等人,2014)。Erdoğan等人(2015)也提出了一种利用组合本德斯切割的精确方法。然而,确切的方法受到问题大小的限制。Dell’Amico 等人(2014)的最佳公式只能有效求解多达50个站点的实例。Erdoğan等人(2015)仅求解了多达60个站点的实例。当站点数量增加时,计算时间呈指数级增长。因此,在求解大型实例时,启发式方法是必不可少的(When the number of stations increases, the computational time increases exponentially. As a result, the heuristic method is essential when solving large instances.
).
已经开发了各种启发式方法来解决BRP,例如大型邻域搜索(Vogel等人,2014,Di Gaspero等人,2016),变量邻域搜索(Rainer-Harbach等人,2013),禁忌搜索(Ho和Szeto,2014),人工蜂群算法(Szeto和Shui,2018),混合遗传算法(Li等人,2016)和化学反应优化(Li等人, 2018). 它们可以在较短的计算时间内提供令人满意的结果。表 2-1 总结了一些优化方法。


 人工蜂群(ABC)算法也属于启发式方法,最早由Karaboga(2005)提出,用于解决单峰和多模态数值优化问题。它已被用于解决各种优化问题,包括有能力的车辆路径问题(例如,Szeto et al., 2011)、灵活的作业车间调度问题(例如, Li et al., 2011)、负载调度问题(例如, Hemamalini and Simon, 2010)、旅行推销员问题(例如, Karaboga and Gorkemli, 2011)等等。感兴趣的读者可以参考Karaboga等人(2014)的论文。ABC算法的广泛应用可能是由于几个原因。首先,ABC算法的机制简单,因此可以直接应用于各种优化问题。其次,它通过不同类型的蜜蜂在多样化和集约化程序之间取得了很好的平衡。第三,它具有与其他方法杂交的灵活性。因此,ABC算法已经应用于BRPs以生成车辆路线(例如,参见Szeto and Shui (2018) ),并且在我们的研究中也被采用
人工蜂群(ABC)算法也属于启发式方法,最早由Karaboga(2005)提出,用于解决单峰和多模态数值优化问题。它已被用于解决各种优化问题,包括有能力的车辆路径问题(例如,Szeto et al., 2011)、灵活的作业车间调度问题(例如, Li et al., 2011)、负载调度问题(例如, Hemamalini and Simon, 2010)、旅行推销员问题(例如, Karaboga and Gorkemli, 2011)等等。感兴趣的读者可以参考Karaboga等人(2014)的论文。ABC算法的广泛应用可能是由于几个原因。首先,ABC算法的机制简单,因此可以直接应用于各种优化问题。其次,它通过不同类型的蜜蜂在多样化和集约化程序之间取得了很好的平衡。第三,它具有与其他方法杂交的灵活性。因此,ABC算法已经应用于BRPs以生成车辆路线(例如,参见Szeto and Shui (2018) ),并且在我们的研究中也被采用
综上所述,自行车重新定位对环境的影响在BRP的文献中缺乏足够的关注,其中大多数仅考虑了自行车用户和系统操作员的收益/成本。破自行车的存在也引起了我们的注意。然而,考虑到这些特性,现有的精确方法不足以解决BRP。鉴于ABC算法在许多其他优化问题中取得了巨大的成功,我们看到了在解决所描述问题方面改进它的潜力。因此,在下一节中,我们将详细解释我们改进版 ABC 算法的算法结构。
3. Problem formulation
在这项研究中,我们考虑了一个具有一个仓库和多个自行车站的 BSS。从公共重新定位运营商的角度制定绿色BRP,尽可能重新平衡BSS,同时减少重新定位过程中产生的CO 2 排放。表示
S
S
S 为站点集,
S
0
S_0
S0为包括depot和stations的节点集。假设该仓库具有无限的容量和自行车供应。假设我们有关于每个站点
i
∈
S
i∈S
i∈S 的完美信息(perfect information),包括其容量
c
i
c_i
ci ,可用自行车
p
i
p_i
pi 和破自行车的初始库存水平
b
i
b_i
bi ,以及可用自行车的目标库存水平
q
i
q_i
qi 。所有节点对
i
,
j
∈
S
0
i,j∈S_0
i,j∈S0 之间的行进距离( travel distances)
d
i
j
d_{ij}
dij 和行进时间(travel times)
t
i
j
t_{ij}
tij 是已知的。自行车站定义为 接送站(pickup station),如果的
p
i
>
q
i
p_i>q_i
pi>qi; 下车站(drop-off station), if
p
i
<
q
i
p_i<q_i
pi<qi;或平衡站(balanced station)
p
i
=
q
i
p_i=q_i
pi=qi 。容量 Q 有限的重新定位车辆从depot(
i
−
0
i-0
i−0),从接送站收集自行车,将自行车运送到下车站,在任何站点收集损坏的自行车 ,并在仓库结束。总重新定位时间(total repositioning time),包括车辆的行驶时间(the travel time of the vehicle )和自行车的搬运时间(handling time of bikes),不应超过时间预算
T
T
T 。自行车的装/卸时间用 表示
L
L
L 。车辆在离开仓库时允许初始负载,或/并带着多余的可用自行车返回仓库。多余的可用自行车和破损的自行车从车辆上卸下到仓库。在重新定位工作期间,可以多次访问车辆段和车站。 假设车辆在车站怠速时关闭发动机,因此仅在行驶过程中产生排放,在怠速期间不会产生排放。绿色BRP旨在为重新定位车辆设计路线和装载说明,以便最大限度地减少与目标库存水平的绝对偏差,自行车损坏引起的损失以及车辆的二氧化碳排放量的加权总和(The green BRP aims to design the route and loading instructions for the repositioning vehicle such that the weighted sum of the absolute deviation from the target inventory level, the penalty induced by broken bikes, and the CO2 emissions of the vehicle are minimized.
)。
数学模型中的参数包括以下内容:

决策变量包括以下内容:

辅助变量包括:

然后,所述问题的数学模型可以表述如下:

p i p_i pi:在站点i好的自行车的初始库存
y i a G y_{ia}^G yiaG:在站点i第a次离开的时候装卸的好的自行车数目
q i q_i qi:在站点i的好的自行车的目标库存
第一项就是与目标库存的偏差值
b i b_i bi:在站点i的坏的自行车的初始库存
y i a B y_{ia}^B yiaB:在站点i第a次离开的时候装卸的坏的自行车数目
第二项就是装载的坏的自行车数目
z a z_a za:第a-1次到第a次之间的排放量
第三项就是碳排量总和
目标(3.1)是尽量减少与目标库存水平的绝对偏差、自行车破损引起的损失以及车辆在重新定位期间产生的二氧化碳排放 2 量的加权总和
须符合:


约束 (3.2) 限制车辆在每个停靠点只能访问一个站点。约束 (3.3)、(3.4) 确保车辆从车辆段开始并在车辆段结束。约束 (3.5)、(3.6)、(3.7) 确保在这些未访问的节点上不会发生加载/卸载操作。此外,损坏的自行车只能在车站收集并运送到仓库。约束 (3.8) 是单调性约束,即我们只从接送站装载自行车,然后将自行车卸载到下车站。约束条件(3.9)、(3.10)、(3.11)表示各站各类自行车的最终库存水平必须不低于零,且各站点库存水平每次访问不超过车站容量。约束 (3.12)、(3.13)、(3.14)、(3.15)、(3.16)、(3.17) 定义离开每个停靠点后的车辆负载。约束 (3.18) 是车辆容量限制。约束 (3.19) 定义了下一站所需的最短额外时间。此额外时间包括 (a-1) th 停靠点和停靠点之间的行驶时间,以及在停靠 th th 点装卸自行车的处理时间。约束 (3.20) 定义第一个停靠点(即仓库)所需的处理时间。约束 (3.21) 意味着车辆必须在时间预算内完成其工作。约束 (3.22) 定义了车辆从 (a-1) th 停靠点行驶到 a th 停靠点时产生的 CO 2 排放量。约束 (3.23)、(3.24)、(3.25)、(3.26)、(3.27)、(3.28)、(3.29) 是域约束。
目标函数中来自于站点
i
∈
S
i \in S
i∈S的与目标水平的绝对偏差
可以通过用辅助变量
δ
i
δ_i
δi 替换并引入其他约束 (3.30)、(3.31)、(3.32) 来线性化:

可以添加以下有效不等式以减少搜索空间并加快该公式的运行时间(Raviv 等人,2013 年):
 约束 (3.33) 意味着如果车辆连续两次停靠进入该站点,则之后仍会停留在那里。约束 (3.34) 保证车辆不会在连续两个停靠点访问同一站点。约束 (3.35) 规定,为 a th 停靠点提供服务的最小额外时间是在此停靠点装卸自行车的处理时间与从任何其他节点到停靠 th 点的最短行驶时间之和。约束 (3.36) 使用从 (a-1) th 停靠点到任何其他节点的最小行驶时间替换了先前约束中的后一项。
约束 (3.33) 意味着如果车辆连续两次停靠进入该站点,则之后仍会停留在那里。约束 (3.34) 保证车辆不会在连续两个停靠点访问同一站点。约束 (3.35) 规定,为 a th 停靠点提供服务的最小额外时间是在此停靠点装卸自行车的处理时间与从任何其他节点到停靠 th 点的最短行驶时间之和。约束 (3.36) 使用从 (a-1) th 停靠点到任何其他节点的最小行驶时间替换了先前约束中的后一项。
约束 (3.19)、(3.35) 和 (3.36) 可以通过使用以下约束 (3.37)、(3.38)、(3.39)、(3.40)、(3.41)、(3.42)、(3.43)、(3.44)、(3.45)、(3.46)、(3.47)、(3.48) 进行线性化:
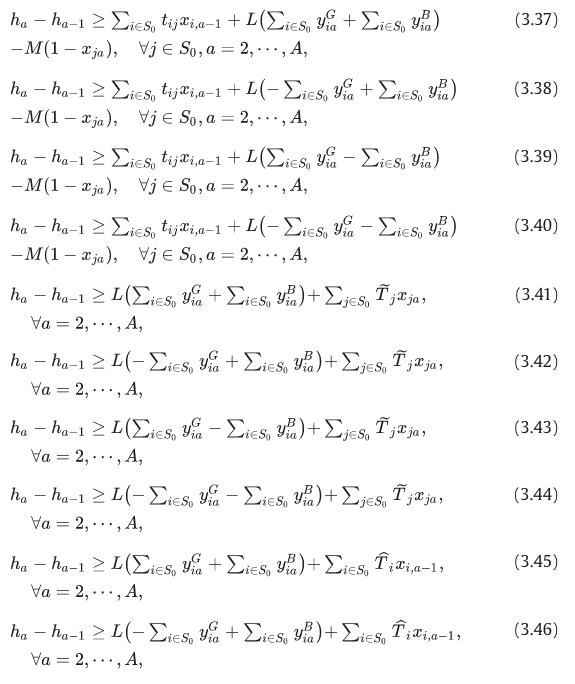









 本文聚焦自行车重新定位问题(BRP),提出增强型人工蜂群(EABC)算法解决破损自行车的静态绿色BRP(GBRP)。考虑可用和破损两种自行车,设计车辆路线与装载指令,最小化目标库存偏差、损坏罚款和二氧化碳排放加权和。实验表明,该算法在求解GBRP上优于其他算法。
本文聚焦自行车重新定位问题(BRP),提出增强型人工蜂群(EABC)算法解决破损自行车的静态绿色BRP(GBRP)。考虑可用和破损两种自行车,设计车辆路线与装载指令,最小化目标库存偏差、损坏罚款和二氧化碳排放加权和。实验表明,该算法在求解GBRP上优于其他算法。


















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








