A Bicycle Origin-Destination Matrix Estimation Based on a Two-Stage Procedure

一、论述
核心问题:如何更有效的进行自行车OD矩阵的估计?
1.1 研究意义:传统模型的局限性
传统交通规划的局限
- 以机动车为中心,忽视非机动车需求(传统的交通规划模型,很大程度上是为汽车量身定做的,自行车略有水土不服,因为行为方式是不同的)
- 缺乏针对自行车网络分析的有效工具(多为统计站点的流量,忽略整个网络上的流量)
- 现有自行车OD估计方法多基于抽样调查或简化模型
现有方法的不足
- 仅能估计部分路段自行车流量,无法全面刻画网络
- 忽略自行车出行的特殊性(如安全、舒适度等)
- 难以满足精细化自行车交通规划的需求
本文的研究价值
弥补现有模型不足,提供更全面的自行车OD估计方法。为自行车交通规划提供更可靠的决策支持。通过两阶段方法,我们能够更准确地估计自行车出行需求,为城市规划提供科学依据。
想了解城市的交通买路,只盯着几个路口观察,未免太片面了。大概是说:统计点的流量,忽略边的流量。总而言之,让我们重视边上的流量吧。它也非常有用,需要去有效的估计。
二、 两阶段模型:核心思想
在第一阶段,采用双约束引力模型(a doubly constrained gravity model)生成初级自行车O-D矩阵(a primary bicycle O-D matix),然后使用PFE( Path Flow Estimator) 来细化初级自行车O-D矩阵.
该模型兼顾了规划数据和观测数据,信息互补。
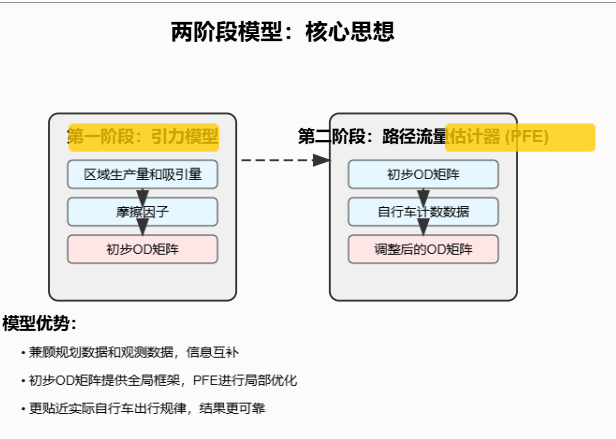

2.1 第一阶段: 引力模型(gravity model)
- 输入规划数据(区域生产量[zonal productions]、区域吸引量[zonal attractions]),利用校准的阻抗函数[impedance function]或者摩擦因子[friction factors],生成初步OD矩阵
利用已有的规划数据,比如各个区域的人口、出行调查数据、就业等信息,来估算大致的出行量
这些数据可以用回归模型或者分类模型等统计方法来完成这个估算。 - 快速、简便,但精度有限
引力模型是基于宏观数据,所以精度有限
步骤简单:- 利用现有规划数据估算区带产量和区带吸引力
- 重力模型中O-D矩阵的初步估计。
普及引力模型
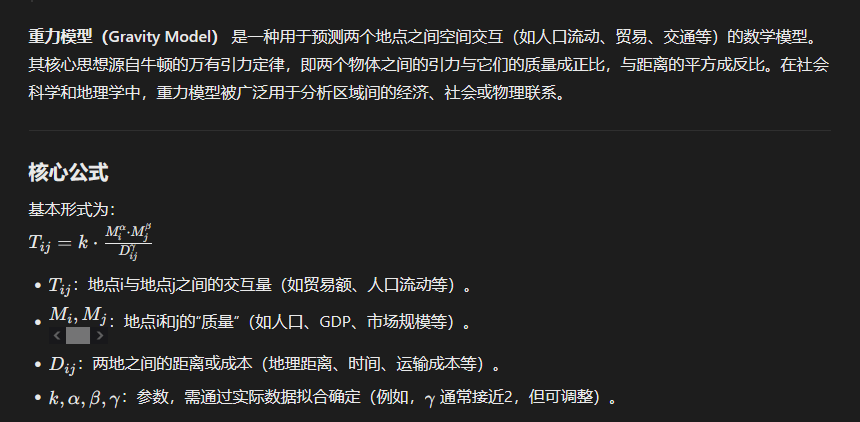
本文中的引力模型


F i j F_{ij} Fij 反应了区域间的空间阻抗或者说出意愿。
此阶段的摩擦因子 F i j F_{ij} Fij和调整因子 K i , K j K_i,K_j Ki,Kj通常需要校准,但有时数据不足,这里简化处理,设置 K i = K j = 1 K_i=K_j=1 Ki=Kj=1.
2.2 第二阶段:路径流量估计器(PFE)
PFE结合在实际道路上观测到的自行车计数数据,对第一阶段生成的初步OD矩阵进行精细调整,并且深入考虑了自行车出行的路径选择行为(精确到边)。
我们开发了一个由路线生成(route generation)和O-D需求调整组成的顺序模型(sequential model)。
步骤一:路径生成
路线生成过程考虑了两个主要因素,即与距离相关的因素(distance-related factors)(例如,route distance)和与安全相关的因素(safety-related factors)(例如,bicycle level of service[BLOS])。

- 考虑距离和安全因素,就可以为每一对OD点生成一系列的自行车路径。
- Route Distance:由路段距离之和和通过路线所经过的交叉口的延迟组成。
由于路段长度单位(例如,公里)和交叉口延迟单位(例如,秒)不同,因此需要在两个测量之间匹配相同的单位。在本文中,延迟(即,分钟)通过转换因子转换为距离单位(即,公里)。路线距离的详细信息,包括方程和描述,可以在[44]中找到。 - BLOS,有许多测量方法可以评估自行车设施的安全性或适用性。关于 BLOS 发展的详细信息可以在 HCM [46]中显示。
- Route Distance:由路段距离之和和通过路线所经过的交叉口的延迟组成。
- 双目标最短路径算法(生成上述路径)
双目标问题一般没有单一的解决方案能够优于其他所有的解决方案。使用帕累托最优原理。
在本文中,我们修改了Climaco [47] 提出的排名方法。首先,使用k最短路径算法根据路线距离属性(即路段距离和交叉口转弯运动惩罚)生成路线,而不超过最大上限(即本研究中的10公里),然后为集合中每个相应的路线计算BLOS分数以确定非支配路线。
步骤二:PFE模型调整
- 输入:初步OD矩阵、观测数据(自行车计数)、路径集—也是3个约束啊
- 输出:调整后的OD矩阵、路径流量、链路流量
目标:找到一组路径流量,是的最终分配到各条路径上的自行车流量,既能满足赶车数据的要求,又能尽可能的接近第一阶段的初步OD矩阵。
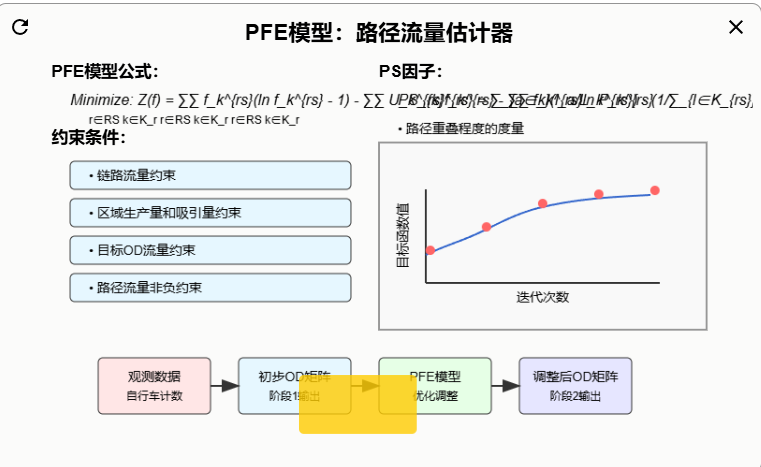
PEF模型公式

目标函数包括三个部分:
- 熵项(鼓励需求分散到多条路径上)
- 系统最优项(倾向于选择总效用最小的路径组合)
- 路径大小PS因子(考虑路径重叠问题,避免过度分配给哪些与其他路径高度重合的路径)
它通过路径长度和路径所经过的链路与其他路径的重叠程度来确定,路径越独特,PS值越高,就越容易被选中。
三、案例研究:温尼伯市自行车OD矩阵估计
研究区域
- 加拿大温尼伯市
- 网络:1067个节点,2555条链路,154个交通分析区域
- 自行车链路:541条(自行车专用车道或者适合骑行)
数据来源
- Emme/4 软件:机动车OD矩阵、链路性能参数
- 温尼伯市政府:自行车网络信息、人口普查数据
研究目的:验证两阶段模型在实际网络中的应用效果
3.1 第一阶段结果
区域生产量和吸引量
- 人口普查数据:自行车通勤者比例 (1.8%)<—2006年的人口普查数据
- 区域生产量:非CBD区域较高
- 区域吸引量:CBD区域较高

初步OD矩阵 - 双重约束引力模型
- 摩擦因子:自行车出行距离
- 调整因子:未使用
3.2 第二阶段结果
路径生成
- 双目标最短路径算法
- 距离上限:10公里(设定上限)
- BLOS上限:7(设定上限)
总共生成了超3万条的有效路径,平均每对OD点有大约5条候选路径。这些路径的平均长度是6.6公里,平均BLOS的等级是3.4,说明生成的路径在距离和安全性上都比较合理。
| 数字 | 含义 |
|---|---|
| 37,263 | 有效路径数 |
| 6.6 | 平均路径距离(km) |
| 3.4 | 平均BLOS |
PFE模型调整
- 观测数据:65个链路自行车计数
Hull等人研究中提供的65个自行车计数点的数据作为观测值。
- 误差界限:30% (自行车计数、区域生产量、吸引量)
不同类型的输入数据,设定了不同的误差界限,前面的为案例
- 流量依赖误差界限 (目标OD流量)
流量越大,允许的误差范围越小
3.3 结果对比:观测值 vs. 估计值
对比指标
- 链路流量
- 区域生产量
- 区域吸引量
- OD需求
对比方法:散点图和均方根误差(RMSE)
结果分析:两阶段模型估计值与观测值吻合度较高
3.4 结果对比:初步OD vs. 调整后OD
结果分析
- 大部分OD对调整幅度较小 (±0.25 trips)
- 95%以上OD对调整幅度小于 ±1.0 trips
- 少部分OD对调整幅度较大 (约2%)
四、结果对比:PSLA vs. PFE 链路流量
结果分析
- CBD区域链路流量调整幅度较大
- 约32%的链路流量差异显著
- PFE模型在链路流量分配上更精细
五、结论和展望
研究结论
- 两阶段模型有效提高了自行车OD矩阵估计精度
- 案例研究表明模型在实际网络中具有应用价值
- PFE模型在链路流量分配上优于传统模型
未来展望
- 参数校准:提高模型精度的关键
- 网络拓扑和自行车设施多样性
- 考虑机动车拥堵和出行模式
- 考虑驾驶技能等个体差异
- 加强数据收集,避免数据不一致性

























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








