阶跃函数（阶跃信号）

听海边涛声

已于 2024-01-29 11:17:22 修改

阅读量8.2k

点赞数 11

文章标签：数学

于 2023-12-27 11:24:17 首次发布

版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

本文链接：https://blog.csdn.net/panghuangang/article/details/135241060

版权

阶跃函数

阶跃函数可以表示为

$f(t)=\left\{\begin{matrix} 0,\; \; \; \; t<0\\ R,\; \; \; \; t\geq 0 \end{matrix}\right.$

更一般的形式，称为“延时的阶跃函数”：

$f(t-t_{0})=\left\{\begin{matrix} 0,\; \; \; \; t<t_{0}\\ R,\; \; \; \; t\geq t_{0} \end{matrix}\right.$

单位阶跃函数

单位阶跃函数用符号 $\varepsilon (t)$ 表示，有的地方也用 $1(t)$ 、或 $u(t)$ 表示：

$1(t)=u(t)=\varepsilon (t)=\left\{\begin{matrix} 0,\; \; \; \; t<0\\ 1,\; \; \; \; t\geq 0 \end{matrix}\right.$

在跳变点 $t=0$ 处，函数值未定义，或在 $t=0$ 处规定函数值 $u(0)=\frac{1}{2}$ 。

单位阶跃函数的波形为

单位阶跃函数的物理背景是，在 $t=0$ 时刻对某一电路接入单位电源（可以是直流电压源或直流电流源），并且无限持续下去。

容易证明，单位斜变函数的导数等于单位阶跃函数。

延时的单位阶跃函数

更一般的形式，称为“延时的单位阶跃函数”：

$1(t-t_{0})=u(t-t_{0})=\varepsilon (t-t_{0})=\left\{\begin{matrix} 0,\; \; \; \; t<t_{0}\\ 1,\; \; \; \; t\geq t_{0} \end{matrix}\right.$

波形为

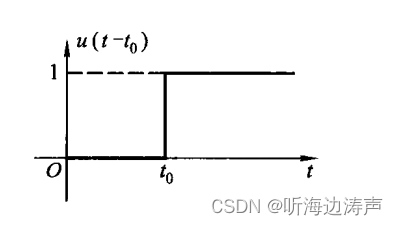
用阶跃信号表示其它信号的接入特性

阶跃信号鲜明地表现出信号的单边特性，即信号在某接入时刻 $t_{0}$ 以前的幅度为零。利用阶跃信号这一特性，可以方便地以数学方式描述各种信号的接入特性。

例如： $f_{1}(t)=(\sin t)u(t)$ 的波形为

$f_{2}(t)=e^{-t}[u(t)-u(t-t_{0})]$ 的波形为

评论

被折叠的条评论为什么被折叠?

到【灌水乐园】发言

查看更多评论

添加红包

成就一亿技术人!

hope_wisdom

发出的红包

实付元

使用余额支付

点击重新获取

扫码支付

钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。