八上：轴对称图形

轴对称图形的确给这个6年级的蒟蒻造成了心理阴影。

这里大概分成2种情况：

无论是什么情况，要根据垂线段最短和对称轴求解。

当然还有一个重要的理论：一个直角三角形中，如果斜边是一个直角边的2倍，那么这个直角边对应的角一定为30°。

怎么证明？其实很容易，只要找来一个90°，60°，30°的三角尺就可以知晓了。

NO.1

第一种用几个字概括：已知对称轴。

给两个动点，给一条角平分线，其中一个动点在角平分线上。

这个时候，不要动平分线上的动点，以角平分线为对称轴，做他的平分点，根据垂线段最短的定理，做一条线段，3点在一条线段才是最短的距离，正是一条底上对应的高。

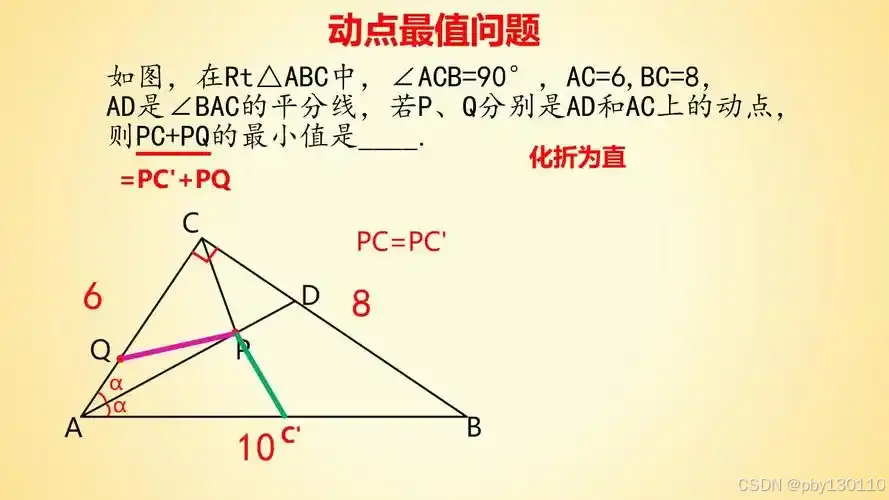
大概如上述图片。

NO.2

第二种用简洁些的语言概括就是未知对称轴。

在这种题型里，大多都是三角形周长最小，注意周长有三条边，通过动点所在的线，设为对称轴，做已知定点的对称点，一定别忘是2个点，周长！周长！

还有将军饮马问题，给一条无限延长的直线l以及与他平行的直线l2，两侧各有一定点A,B，l上有一动点m，l2上有一动点n，m，n必须在一条线段上，这条线段必须与l，l2垂直。

 对于这种问题，将AM平移至N点，形成A1N // AM,变成了平行四边形，此题只是求A1N+NB的长度了，两点之间，线段最短，连接A1和B，在l2上取交点，就是N的位置，根据这个再去找M的位置即可。

这里如图所示，在直线l上有线段MN，长度为1cm，现有两点AB，问如何移动位置才能使AM+MN+NB的长度最短。

MN的长度为定值，我们不必管他，将题目简化为求AM+NB的长度最短。

两点在同侧，无法直接运用两点之间线段最短求解，那就根据l为对称轴，做A的对称点A1，这样就是一个标准将军饮马问题了， 我们令NB平移至M点，得到B1M // NB，问题简化为求A1M+B1M的最短路径问题了，这是使用定理的绝佳时期，直接两点之间，线段最短，将A1与B1相连接，A1B1线段与直线l的交点便是M1，M1向后移1cm便可。

此类题目是将军饮马问题的进阶，通过对称求解。

补充一个知识点：在直角三角形中，斜边上中线的长度是斜边长度的一半。

如有初二大佬耳提面命，吾将洗耳恭听。