二阶预测误差排序的RDH方法

用于可逆数据隐藏的二阶预测误差排序

摘要

可逆数据隐藏（RDH）方案通过生成高度集中的预测误差直方图来相互竞争，这通常通过结合预测策略和排序技术实现。排序技术旨在估计每个像素的局部上下文复杂度，以优化嵌入顺序。本文提出一种用于可逆数据隐藏的新型二阶预测与排序技术。首先，通过利用当前通道和参考通道的预测误差进行通道间二次预测，获得预测误差。实验表明，该预测方法能够生成更尖锐的二阶预测误差直方图。然后，我们引入一种新颖的二阶预测误差排序（SOPS）算法，该算法充分利用来自其他颜色通道的边缘信息以及相邻像素之间的高相关性特征，从而更好地反映当前像素的纹理复杂度。实验结果表明，所提出的方法在预测精度和整体嵌入性能方面均显著优于此前的先进方法。

关键词

可逆数据隐藏 · Channel相关性 · Second顺序预测误差

1 引言

可逆数据隐藏(RDH)[1],作为信息隐藏的一个特殊分支，在过去几年中受到了广泛关注。它不仅关注用户的嵌入数据，还关注载体本身。RDH能够从标记内容中精确且无损地提取原始载体数据和嵌入的信息。这项重要的数据隐藏技术在许多领域（如医学图像）中提供了有价值的功能保护、认证和篡改载体恢复、数字媒体版权保护、军事图像和法律领域，其中在数据提取过程中载体不能受损。数字图像的可逆数据隐藏框架如图1所示。

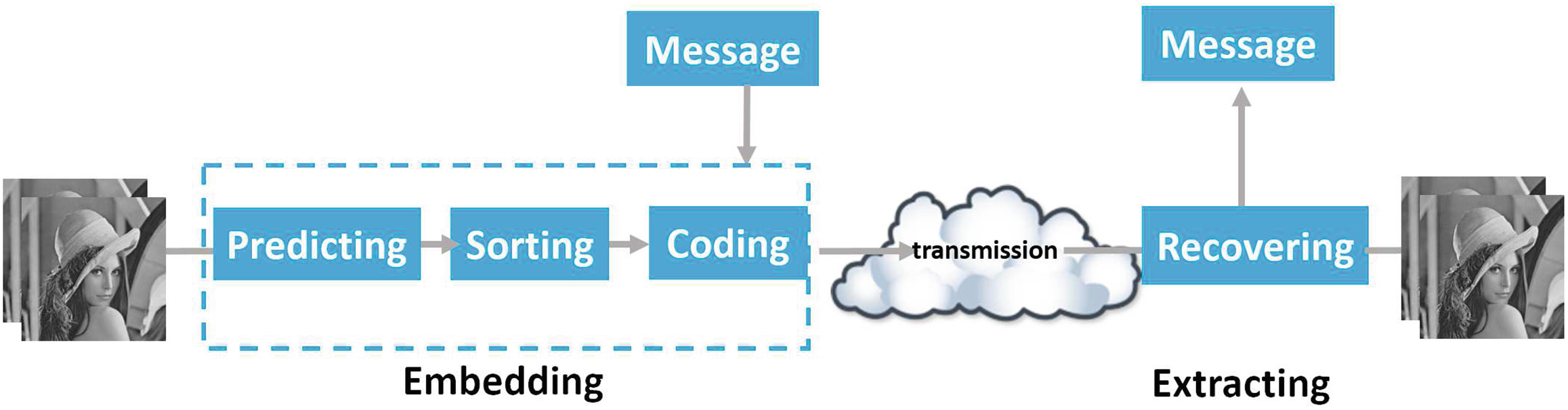
为了提高可逆数据隐藏的效率，研究人员在过去几十年中提出了许多方法。一般来说，预测和排序在可逆信息隐藏过程中起着重要作用。预测的重点是如何更好地利用像素间相关性以获得尖锐分布的预测误差；而排序技术则侧重于利用相邻像素之间的相关性来优化嵌入顺序。

预测精度的提升对于基于直方图平移和差值扩展的可逆数据隐藏（RDH）方案都至关重要。已有一些预测器被提出，如中值边缘检测（MED）、梯度自适应预测（GAP）以及差分自适应游程编码（DARC）。MED预测器在当前位置右侧存在垂直边缘时倾向于选择下方的垂直相邻像素，在其下方存在水平边缘时选择右侧相邻像素，若未检测到边缘则选择上下文像素的线性组合。

GAP算法根据局部梯度对相邻像素进行加权，并将边缘分为三类：强、中、弱，利用七个相邻像素来估计未知像素值。DARC是一种非线性自适应预测器，使用三个相邻像素来估计未知像素。Dragoi和Coltuc提出了用于可逆数据隐藏的扩展梯度选择与加权（EGBSW）方法。EGBSW算法采用四个线性预测器，通过选定梯度对应的预测值之间的加权和来计算输出值，从而获得最终的预测值。

排序[5,6]是利用相邻像素间相关性以优化嵌入顺序的一个基本步骤，因此排序是提高嵌入容量和视觉质量的基础。Kamstra和Heijmans[7]通过排序引入了相较于先前方法的显著性能优势，他们通过有序排列像素对来减小位置映射大小。萨赫涅夫等人[5]使用局部方差值对预测误差进行排序，将区域按局部方差值升序排列，优先在具有较低局部方差值的更平滑的区域进行嵌入。但在某些情况下，这种方法并不能直接达到精确效果。例如，Afsharizadeh[6]在萨赫涅夫等人的工作[5]基础上，采用一种本文提出的高效排序方法进行了扩展技术，这是一种由更精确的排序过程得出的新排序度量。Ou[8]提出了一种简单高效的排序方法，通过计算局部复杂度来进行排序，该局部复杂度是4×4大小邻域中对角空白像素之间绝对差值的总和。较小的局部复杂度表明该像素对位于平滑图像区域，应优先用于数据嵌入。然而，上述算法未考虑预测误差分布的特性。

然而，我们注意到现有的可逆数据隐藏研究通常集中在灰度图像上。在现实生活中，广泛使用的是彩色图像。近年来，彩色图像的可逆数据隐藏在[9,10]中是一个鲜有研究的课题。考虑到颜色通道之间存在相关性，Li等[11]提出了一种基于预测误差扩展的可逆数据隐藏算法，该算法通过利用另一个通道的边缘信息来提高某一颜色通道的预测精度。通过这种方式，统计上降低了预测误差熵。基于彩色图像的通道间相关性，Li等[11],研究了一种新的通道间预测方法，并提出了一种相应的可逆数据隐藏算法。

在本文提出的方法中，通过利用当前通道和参考通道的预测误差进行通道间二次预测，得到预测误差。实验表明，该预测方法能够生成更尖锐的二阶预测误差直方图。接着，我们将引入一种新颖的二阶预测误差排序（SOPS）算法，该算法充分利用了来自另一颜色通道的边缘信息以及相邻像素之间的高相关性，从而更好地反映当前像素的纹理复杂度。实验结果表明，所提出的方法在预测精度和整体嵌入性能方面均显著优于此前的先进方法。

本文的组织结构如下。第2节介绍了本文提出的用于可逆数据隐藏的二阶预测误差排序算法。第3节展示了使用该技术进行的仿真及获得的结果。第4节根据结果简要得出结论。

2 用于彩色图像的二阶预测误差排序（SOPS）

2.1 基于颜色通道间相关性的二阶预测误差

显然，图像的边缘在人类视觉系统（HVS）中起着至关重要的作用，其特征表现为强度上的突变。如何利用这一特性进行像素预测非常重要。针对可逆数据隐藏（RDH），已提出的一些预测器，如中值边缘检测（MED）和梯度自适应预测（GAP）[2]，在粗糙区域可能效果不佳。在这种情况下，由于粗糙区域沿梯度方向的像素差异较大，预测误差通常与像素值相差较大。然而，更精确的预测误差可以通过沿边缘方向的像素获得。特别是对于彩色图像，我们可以充分利用从另一个颜色通道获得的边缘信息以及相邻像素之间的高相关性。在[11], Li等指出，从不同颜色通道提取的边缘信息彼此相似。因此，如果在一个颜色通道中检测到边缘，则在其他通道的相同位置也会存在相同的边缘。

在每个通道中，我们使用Sachnev等人et al.[13],提出的双层嵌入方法，将所有像素划分为阴影像素除集和空白集（见图2）。在第一轮中，阴影集用于嵌入数据，空白集用于计算预测值。而在第二轮中，空白集用于嵌入，阴影集用于计算预测值。由于这两层嵌入过程在本质上相似，我们仅以阴影层为例进行说明。

设pc和pr分别表示像素p在当前通道和参考通道中的样本值。为了判断该像素是否位于图像边缘，我们需要计算两个参数。平均距离Davg和方向距离Ddir可由以下方式给出

$$
D_{avg} = \left| \sum_{k=1}^{8} \alpha_k^{avg} p_k^r - p_r \right|
$$

其中$\alpha_k^{avg}(k = 1,2,… 8)$是八个邻居$p_1^r = p_{nw}^r, p_2^r = p_n^r, p_3^r = p_{ne}^r, p_4^r = p_w^r, p_5^r = p_e^r, p_6^r = p_{sw}^r, p_7^r = p_s^r, p_8^r = p_{se}^r$的系数。如果位于平滑区域，则平均距离Davg应较小；相反，如果pr位于粗糙区域，则Davg会很大。然而，如何确定图像中边缘的方向？接下来，我们通过计算方向距离Ddir来确定方向，如下所示

$$
D_{dir} = \min\left{ \left| \frac{p_w^r + p_e^r}{2} - p_r \right|, \left| \frac{p_n^r + p_s^r}{2} - p_r \right|, \left| \frac{p_{nw}^r + p_{se}^r}{2} - p_r \right|, \left| \frac{p_{ne}^r + p_{sw}^r}{2} - p_r \right| \right}
$$

其中$\left|\frac{p_w^r + p_e^r}{2} - p_r\right|$、$\left|\frac{p_n^r + p_s^r}{2} - p_r\right|$、$\left|\frac{p_{nw}^r + p_{se}^r}{2} - p_r\right|$和$\left|\frac{p_{ne}^r + p_{sw}^r}{2} - p_r\right|$分别表示四个边缘方向，即水平、垂直、对角线和反对角线。取其中最小值作为Ddir。边缘表现为强度的跳跃，例如，最小值意味着像素位于图像的边缘上。

可以用来判断参考样本是否位于$|D_{avg} - D_{dir}|$边缘区域。考虑到所有[11],颜色通道在$|D_{avg}-D_{dir}|$中的边缘分布相似，像素的预测应考虑从另一通道获得的边缘信息。因此，我们可以利用pc来分类当前样本的位置$|D_{avg}-D_{dir}|$。如果pc接近于零或非常小，则意味着当前样本pc位于图像的平滑区域。在这种情况下，从其他通道获取的边缘信息是无用的，我们可以充分利用$|D_{avg} - D_{dir}|$的八个邻居。另一方面，如果ρ大于预设阈值pc，我们认为

$$
\hat{p} c =
\begin{cases}
\left\lfloor \frac{p_w^c + p_e^c + p_n^c + p_s^c}{4} + 0.5 \right\rfloor & |D {avg} - D_{dir}| \leq \rho, \
\left\lfloor P(p_k^c|D_{dir}) + 0.5 \right\rfloor & |D_{avg} - D_{dir}| > \rho.
\end{cases}
$$

其中$P(p_k^c|D_{dir})$根据Ddir。例如，当$D_{dir} = \left|\frac{p_w^r + p_e^r}{2} - p_r\right|$时，则$P(p_k^c|D_{dir}) = \frac{p_w^r + p_e^r}{2}$。当$D_{dir} = \left|\frac{p_n^r + p_s^r}{2} - p_r\right|$时，则$P(p_k^c|D_{dir}) = \frac{p_n^r + p_s^r}{2}$。当$D_{dir} = \left|\frac{p_{nw}^r + p_{se}^r}{2} - p_r\right|$时，则$P(p_k^c|D_{dir}) = \frac{p_{nw}^r + p_{se}^r}{2}$。当$D_{dir} = \left|\frac{p_{ne}^r + p_{sw}^r}{2} - p_r\right|$时，则$P(p_k^c|D_{dir}) = \frac{p_{ne}^r + p_{sw}^r}{2}$。

然后，我们可以得到基于颜色通道间相关性的一阶预测误差如下

$$
\Delta e_c = p_c - \hat{p}_c \quad (3)
$$
$$
\Delta e_r = p_r - \hat{p}_r \quad (4)
$$

其中$\Delta e_c$是当前通道中的一阶预测误差，$\Delta e_r$是参考通道中的一阶预测误差。

接下来，通过以下方式计算二阶预测误差

$$
\Delta^2 e = \Delta e_c - \Delta e_r \quad (5)
$$

当图像的平滑区域中的像素彼此相似时，一阶预测误差$\Delta e_c$和$\Delta e_r$接近于零。因此，二阶预测误差也接近于零。另一方面，当像素位于粗糙区域时，一阶预测误差$\Delta e_c$和$\Delta e_r$相对较大。然而，考虑到所有颜色通道具有相似的边缘分布，并结合从另一个通道获得的边缘信息，二阶预测误差会变得更小。因此，得到二阶预测误差序列$\Delta^2 e = (\Delta^2 e_1, \cdots, \Delta^2 e_N)$。

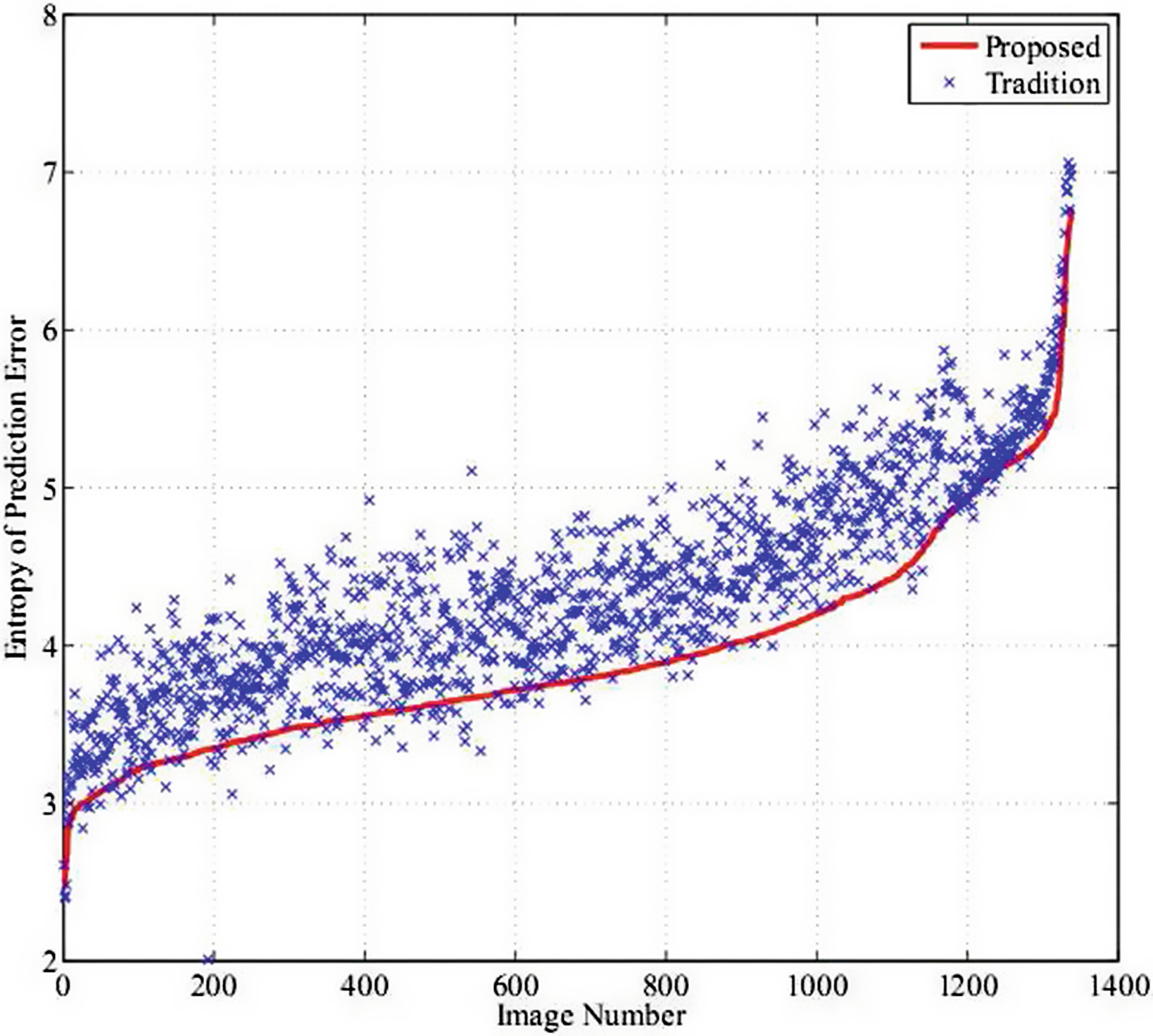
如何评估预测方法？可以使用预测误差的熵值来评估本文提出的预测方法的性能。如果熵值越小，则预测性能越好。反之，如果熵值越大，则预测的性能越差。本文实验中采用了UCID（无压缩彩色图像数据库），该数据库包含超过1300幅无压缩彩色图像。从图3中可以看出，本文提出方法的熵值小于MED、菱形以及基于颜色通道相关性的一阶预测误差等传统方法对应的熵值。

2.2 基于广义正态分布的二阶预测误差排序

广义“误差”分布是正态分布的一种广义形式，它具有天然的多元形式，并且其参数峰度在上方无界，同时包含与正态分布和双指数分布完全相同的一些特例[21]。鉴于预测误差的概率密度函数（PDF）服从广义正态分布或高斯分布，我们考虑使用该模型来描述图3中的预测误差。广义正态分布密度函数由Nadarajah定义[9]。

$$
f(\Delta e|u, \alpha, \beta) = \frac{\beta}{2\alpha\Gamma(1/\beta)} \exp\left(-\left|\frac{\Delta e - u}{\alpha}\right|^\beta\right), \quad (6)
$$

其中$\Delta e$是均值为$u$、方差为$\sigma^2$的预测误差。$\alpha = \sqrt{\sigma^2 \Gamma(1/\beta)/\Gamma(3/\beta)}$是尺度参数，起到决定PDF宽度的方差作用，而$\beta > 0$称为形状参数，用于控制众数附近的衰减速率（$\beta$越高，衰减越慢）。

的分布)

率）。$\Gamma(.)$表示伽玛函数，使得$\Gamma(t) = \int_0^\infty x^{t-1} \exp(-x) dx$。容易看出，当$\beta = 2$时，式（6）退化为正态分布，当$\beta = 1$时，退化为拉普拉斯分布。

根据公式(6)，我们可以很容易得到$\Delta e_c \sim GND(u_c, \alpha_c, \beta_c)$和$\Delta e_r \sim GND(u_r, \alpha_r, \beta_r)$。然后$\Delta^2 e = \Delta e_c - \Delta e_r$可以表示为

$$
f(\Delta^2 e) = -\int_{-\infty}^{+\infty} f_{\Delta e_c - \Delta e_r}(\Delta e_c, \Delta^2 e - \Delta e_c) d\Delta e_c = -\int_{-\infty}^{+\infty} \frac{\beta_c \beta_r}{4\alpha_c \alpha_r \Gamma(1/\beta_c)\Gamma(1/\beta_r)} \times \exp\left(-\left|\frac{\Delta e_c - u_c}{\alpha_c}\right|^{\beta_c} - \left|\frac{\Delta^2 e - \Delta e_c - u_r}{\alpha_r}\right|^{\beta_r}\right) d\Delta e_c \quad (7)
$$

根据公式(7)，似乎不存在闭式表达式。然而，为了简化并降低问题的复杂性，我们取$\beta = 1$作为广义正态分布的一个特例。当$\beta = 1$时，对应于如下拉普拉斯分布

$$
f(\Delta^2 e) = -\int_{-\infty}^{+\infty} f_c(\Delta e_c)f_r(\Delta^2 e - \Delta e_c)d\Delta e_c = \frac{\alpha_c}{2(\alpha_c^2 - \alpha_r^2)} \exp\left(-\frac{|\Delta^2 e - (u_c - u_r)|}{\alpha_c}\right) - \frac{\alpha_r}{2(\alpha_c^2 - \alpha_r^2)} \exp\left(-\frac{|\Delta^2 e - (u_c - u_r)|}{\alpha_r}\right) \quad (8)
$$

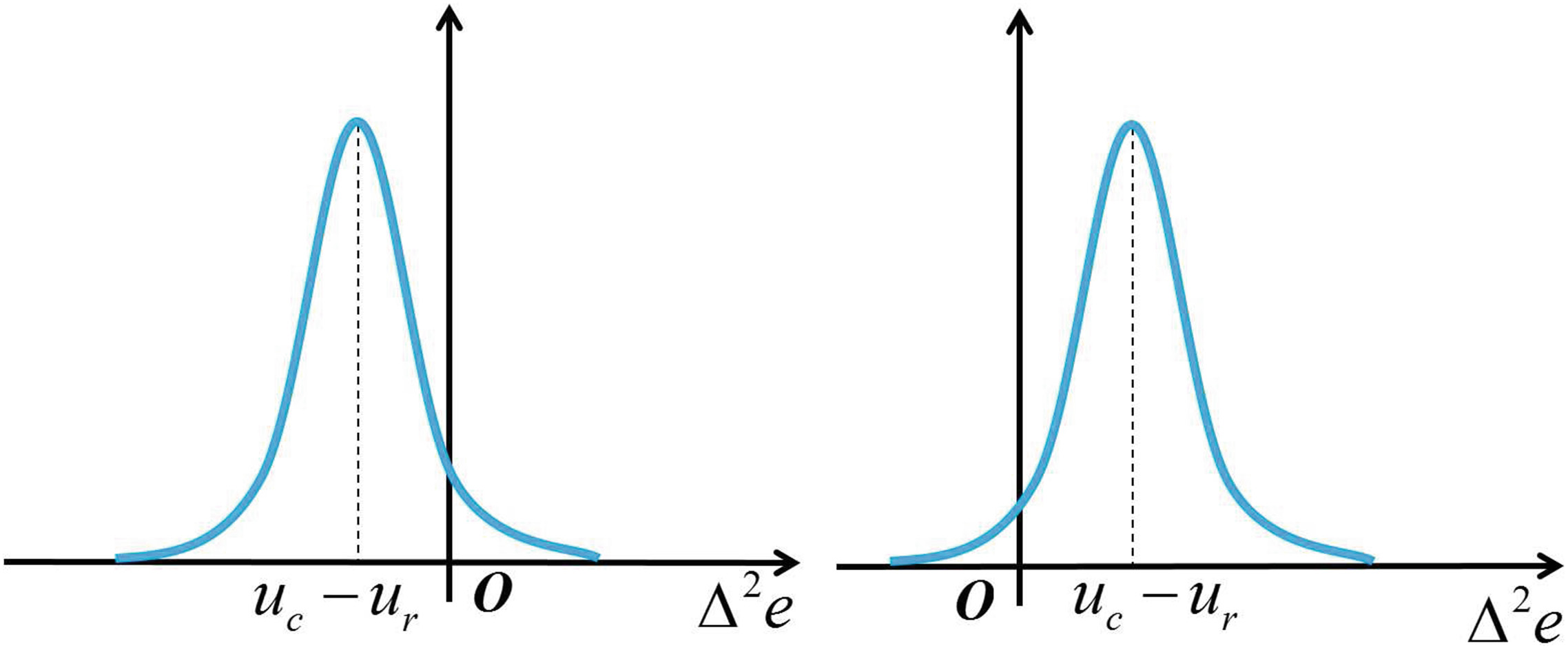
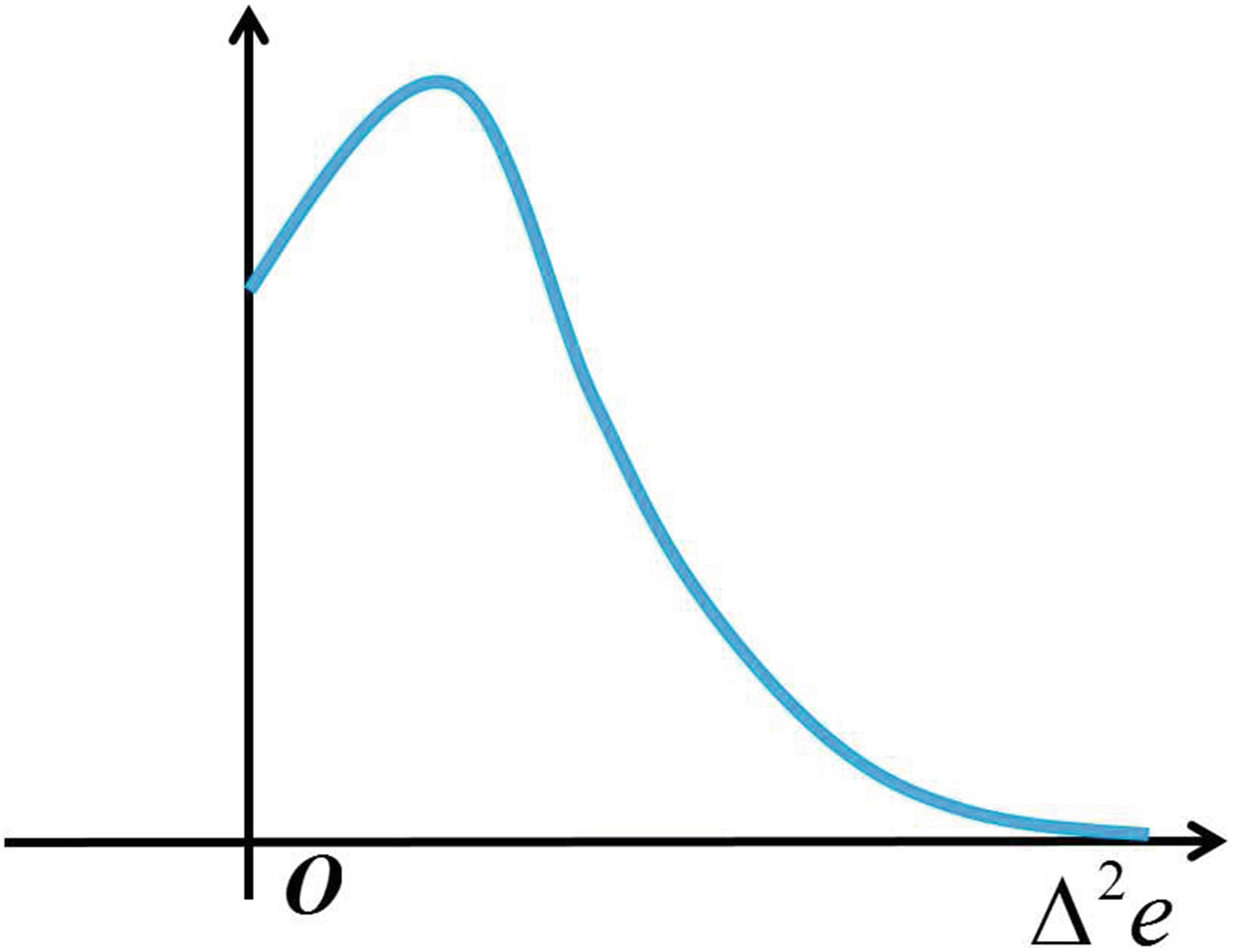
很容易看出，$f(\Delta^2 e)$是在不同权重下具有相同均值的两个拉普拉斯分布之间的差异。$u_c - u_r$二阶预测误差的概率密度函数(PDF)如图4所示。如图4所示，$u_c - u_r$到y轴的距离可用于反映二阶预测误差的准确性。距离越小，预测的准确性越高。由于距离用于衡量预测误差的准确性，因此我们可以得到一个新的函数$\Phi(\Delta^2 e) = |f(\Delta^2 e)|$(图5)。

的分布)

函数$\Phi(\Delta^2 e)$的分布可由下式给出。显然可以看出，函数$E[\Phi(\Delta^2 e)]$的期望与$u_c - u_r$呈正相关。因此它可用于表征二阶预测误差的准确性。

例如，如果$E[\Phi(\Delta^2 e]$
$E[\Phi(\Delta^2 e)]$较小，则说明预测误差的分布更加集中，预测的准确性更高。为了进一步量化这种准确性，我们引入了一个新的排序度量$E[\Phi(\Delta^2 e)]$，它综合反映了像素的局部上下文复杂度和预测误差的集中程度。

具体而言，$E[\Phi(\Delta^2 e)]$依赖于参数$u_c, u_r, \alpha_c, \alpha_r$。这些参数分别代表当前通道和参考通道预测误差的均值与尺度。当这些参数越小，意味着预测误差越接近于零且分布越紧凑，因此预测性能越好。由此，$E[\Phi(\Delta^2 e)]$可以作为一个有效的排序指标，用于指导数据嵌入的优先级。

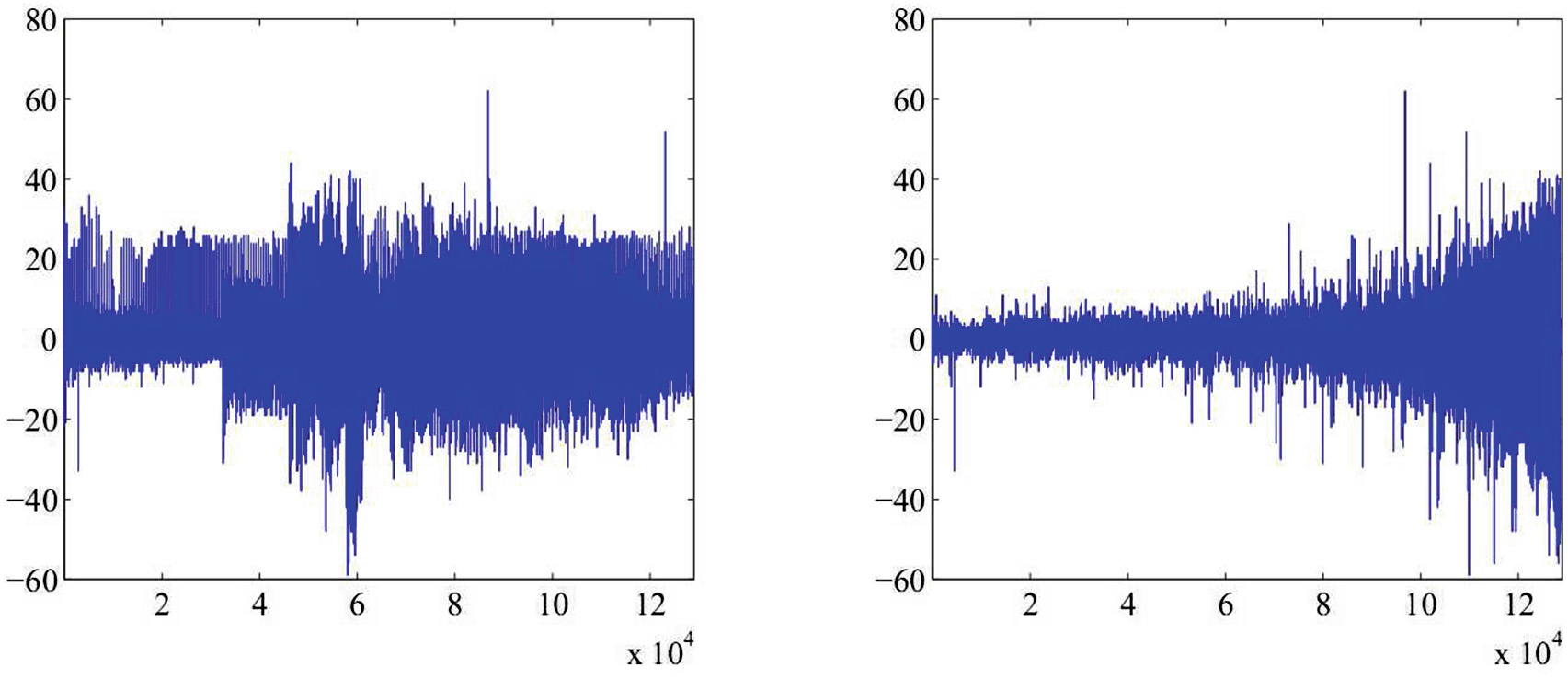
通过设定一个阈值$\lambda$，我们筛选出满足$E[\Phi(\Delta^2 e)] \leq \lambda$的像素进行数据嵌入，其余像素则被跳过。对于给定的嵌入容量$R$，$\lambda$被动态调整为能够容纳所需数据量的最小值。嵌入过程从$E[\Phi(\Delta^2 e)]$最小的预测误差开始，依次处理后续像素，直至完成全部数据嵌入。如图6所示，左侧为Lena图像在排序前的预测误差分布，误差幅度较大且分散；右侧为使用本文方法排序后的结果，明显可见低误差区域被优先排列，熵值更低的部分集中在前端。由于信息被嵌入到预测最准确的区域，图像的质量损失显著减少，视觉效果得以大幅提升。

3 应用、实验与分析

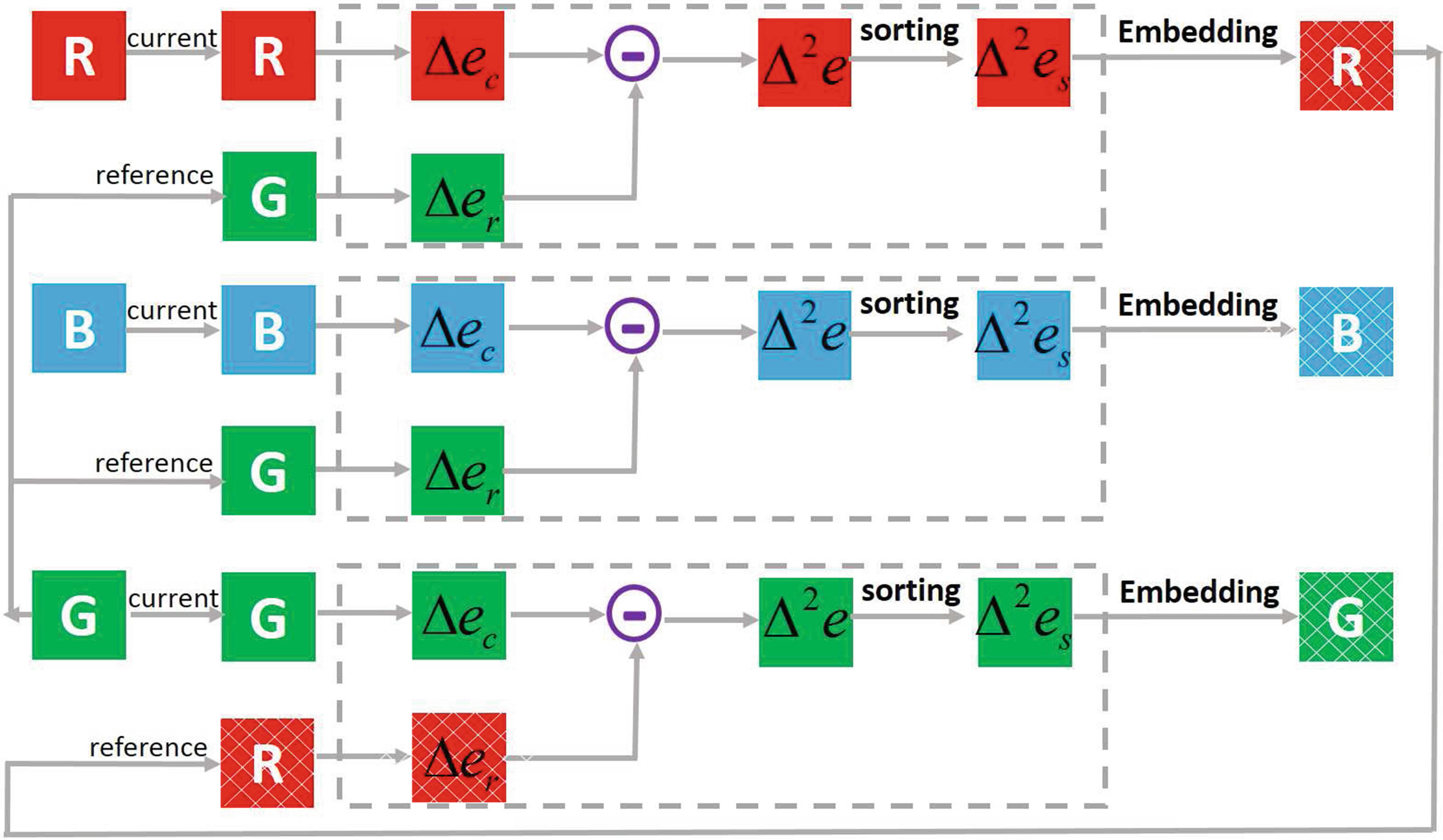
在本节中，我们将二阶预测误差排序（SOPS）算法应用于Li等人的[11]方法。需要强调的是，嵌入和提取过程与[11]中的算法相同。我们仅在实验中替换或添加了预测和排序算法。然后，所提出的用于可逆数据隐藏的SOPS框架如图7所示。如图7所示，我们首先以绿色通道为参考通道，将数据隐藏到红色和蓝色通道中。当将数据隐藏到绿色通道本身时，参考通道为已标记的红色通道。彩色图像的二阶预测误差排序的嵌入过程和提取过程如下：

我们在配备英特尔酷睿i3处理器和4GB内存的计算机上实现了这些方法。程序开发环境为基于微软Windows 7操作系统的MATLAB R2011b。在实验中，我们采用了四个彩色图像（参见图8）用于通过嵌入容量失真曲线测试我们提出的RDH算法的性能。在图8中，前两个标准图像是以TIFF格式保存的，尺寸为$512 \times 512$。而两个柯达图像是数据库中保存的第一个和最后一个（http://r0k.us/graphics/kodak/），采用PNG格式，尺寸为$512 \times 768$。我们的方法通过与Li等人的[11], Li等人[12], Sachnev等人[13], 阿拉塔尔[14], Hu等人[15], 杨和黄[16]这六项近期工作进行比较来评估。对于我们的方法，嵌入量从100,000比特变化到300,000比特或600,000比特，步长为50,000比特。

算法1 用于彩色图像可逆数据隐藏的二阶预测误差排序嵌入过程。

输入 : 当前通道中的一阶预测误差 $\Delta e_c$。参考通道中的一阶预测误差 $\Delta e_r$。嵌入率 $R$。
输出 :
1：通过$\Delta^2 e = \Delta e_c - \Delta e_r$计算二阶预测误差。
2：根据对应的$E[\Phi(\Delta^2 e)]$将二阶预测误差按升序排序。处理满足$E[\Phi(\Delta^2 e)] \leq \lambda$的预测误差以嵌入有效载荷。
3：通过J. Li et al.[11]方法将输入数据隐藏到排序后的序列中。使用LSB替换，将$\lambda$、压缩位置图大小和消息大小嵌入到某些首行像素的最低有效位中。
4：return 此步骤完成后，阴影层嵌入即完成。标记的二阶预测误差序列$\Delta^2 e’ = (\Delta^2 e’_1, \cdots, \Delta^2 e’_N)$。

算法2 彩色图像可逆数据隐藏的二阶预测误差排序提取过程。

输入 : 由$\Delta^2 e$标记的二阶预测误差。参考通道中的一阶预测误差$\Delta e_r$。
输出 :
1：通过读取某些首行像素的最低有效位，确定$\lambda$的值、压缩位置图大小和消息大小。
2：使用相同的预测和扫描顺序获得标记的二阶预测误差序列$\Delta^2 e’ = (\Delta^2 e’_1, \cdots, \Delta^2 e’_N)$。
3：这些预测误差的恢复是通过J. Li et al.[11]中所提出的方法的逆映射实现的。
4：return 恢复原始二阶预测误差序列$\Delta^2 e = (\Delta^2 e_1, \cdots, \Delta^2 e_N)$。然后，恢复原始阴影像素。

从图9可以看出，我们的方法与六项近期工作进行了对比评估。比较结果如图9(a)–(d)所示。根据实验结果可知，所提出的方法优于这些最先进的方法。无论测试图像或容量如何，我们的方法都能提供更高的峰值信噪比。与Li等人的方法[11]相比，实验结果表明，我们的方法在Lena图像上峰值信噪比平均提升0.65dB，在芭芭拉图像上提升3.63dB，在柯达‐01图像上提升2.66dB，在柯达‐24图像上提升0.91dB。与Li等人[11]的方法相比，我们的方法平均获得了1.96dB的峰值信噪比增益；与Sachnev等人[5]的方法相比，峰值信噪比的增益更高（见图10）。

4 结论

本文提出了一种新颖的用于可逆数据隐藏的二阶预测与排序技术。首先，通过利用当前通道和参考通道的预测误差进行通道间二次预测，得到预测误差。当图像处于平滑区域时，像素之间相互相似，一阶预测误差接近于零，因此二阶预测误差也接近于零。另一方面，当像素位于粗糙区域时，一阶预测误差相对较大。然而，考虑到所有颜色通道具有相似的边缘分布，并结合从另一通道获取的边缘信息，二阶预测误差会变得更小。实验表明，该预测方法能够产生更尖锐的二阶预测误差直方图。随后，我们将介绍一种新颖的二阶预测误差排序方法。

(SOPS)算法，该算法充分利用了从另一颜色通道获得的边缘信息以及相邻像素之间的高相关性。因此，它能够反映像素的局部上下文复杂度和预测误差的预测准确性。实验结果表明，所提出的方法相较于Li等人的[11], Li等人[12], Sachnev等人[13], 阿拉塔尔[14], Hu等人[15], 杨和黄[16]六项近期工作取得了更好的结果。