浅析红黑树

红黑树是一棵二叉搜索树，只是它在以前的二叉树的基础上对每个结点增加了一个特性：颜色特性，或为红色或为黑色。红黑树通过保证最长路径不超过最短路径的两倍来保证近似平衡。
红黑树是满足以下特点：
1）每个节点不是红色就是黑色；
2）根节点是黑色的；
3）如果一个结点是红色，它要么没有子节点，要么子节点是黑色。（不能由连续 的红色结点）
4）对于每一个结点，从该节点到叶子结点的路径上黑色结点的个数都是相等的。
满足这个性质，怎么就可以保证最长路径不超过最短路径的两倍？？？
每条路径上黑色结点数量相等，并且红色结点不能连续，加入每条路径上黑色结点的数量是n，那么最短路径上结点数是n，最长路径上结点数是2*n（n个红色结点，每个红色结点都插在黑色结点之间，保证红色结点不连续），这样就保证最长路径不超过最短路径的两倍。
插入
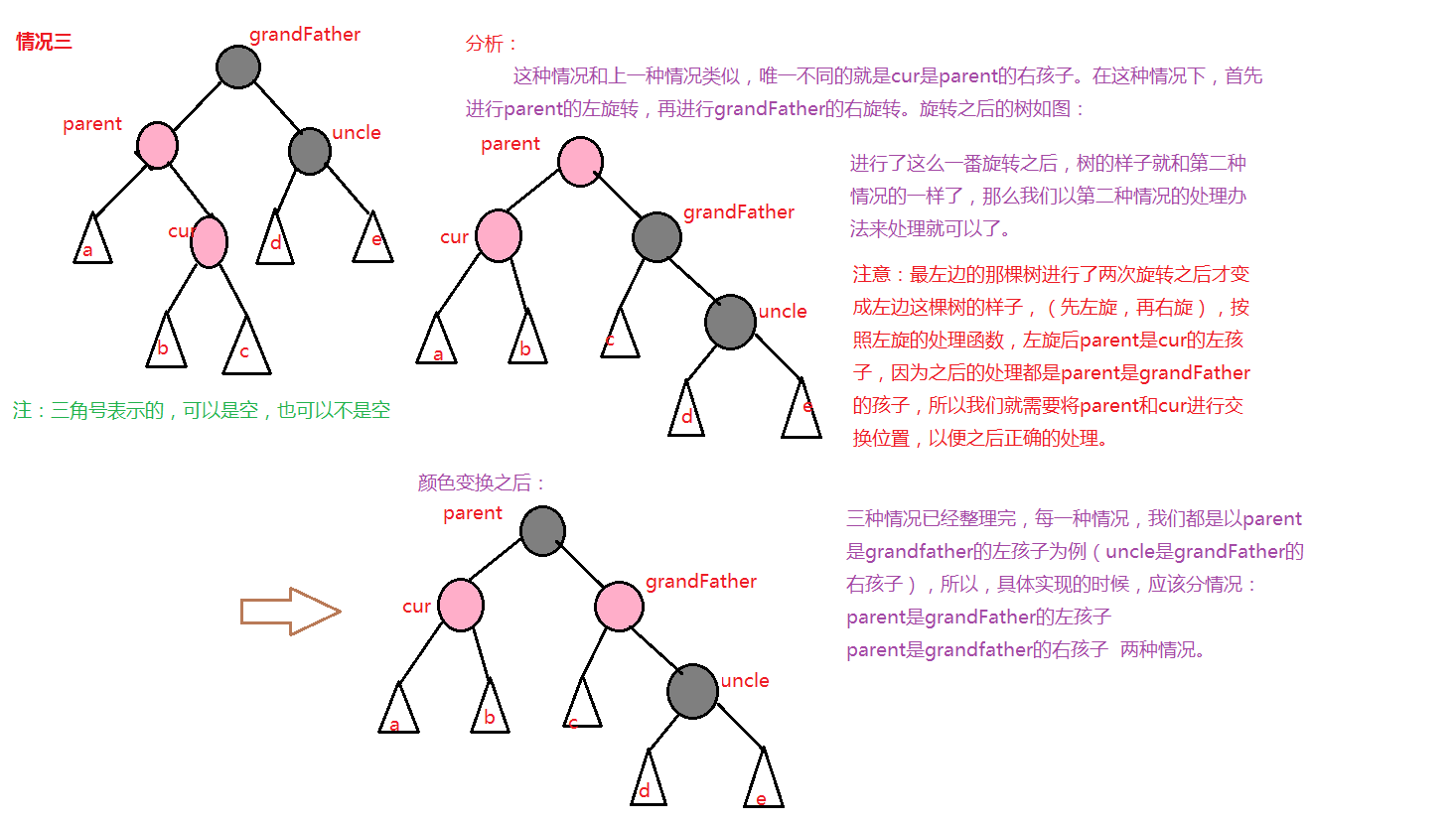
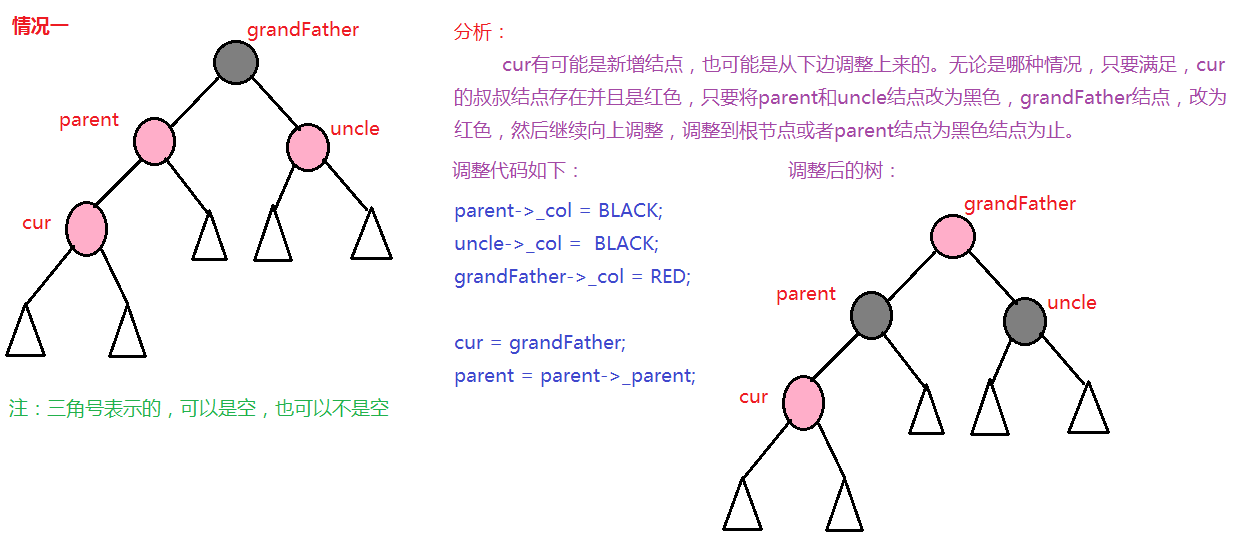
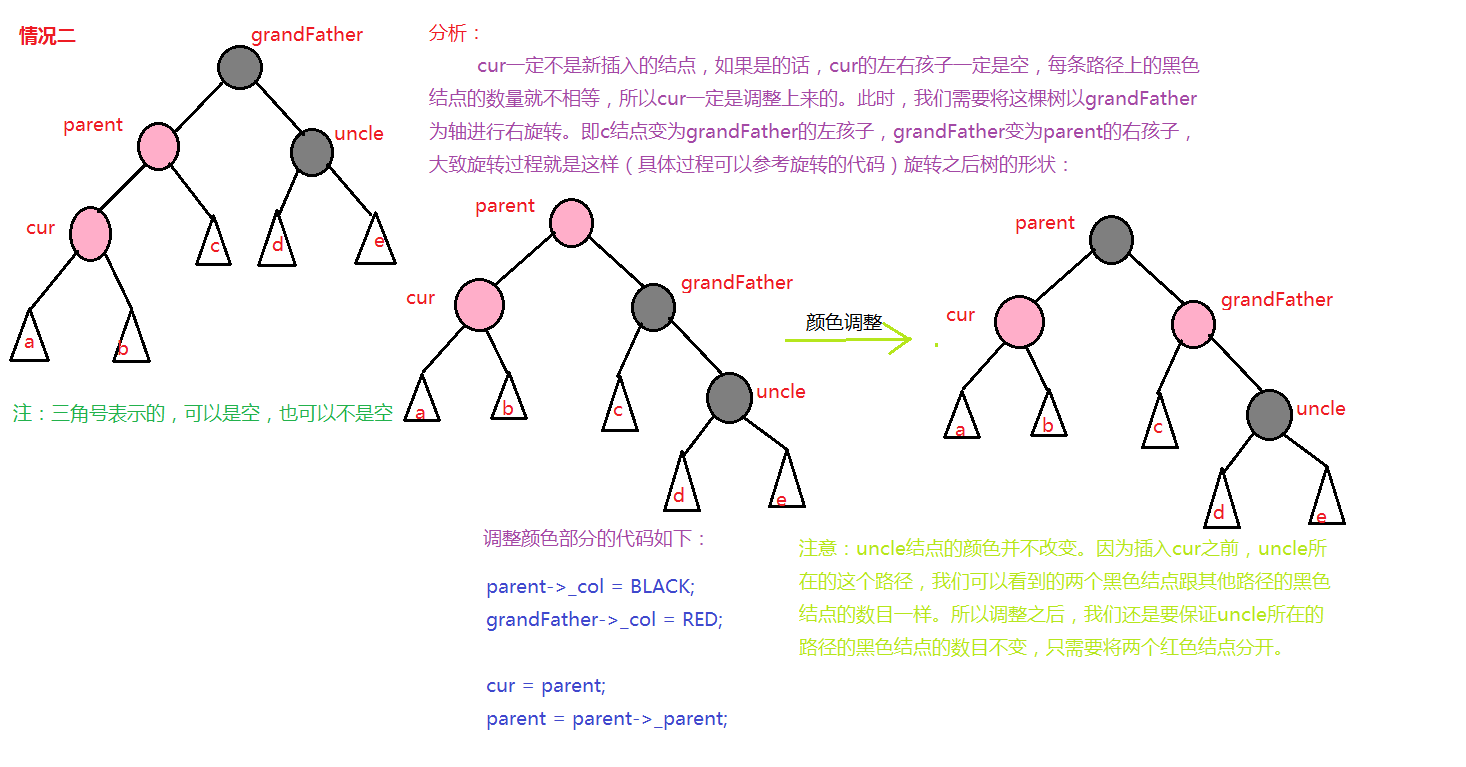
由于红黑树同样是一棵二叉搜索树，所以必须满足二叉搜索树的性质，即左子树的值小于根节点，右子树的值大于根节点。所以插入的时候必须先找到合适的位置。然后利用旋转来保证这棵树 成为红黑树。插入结点时，先让这个结点为红色，然后进行处理；假设给成黑色，这样就一下子改变了路径上黑色结点的个数，树就不是红黑树。所以默认给成红色。下边给出插入一个结点之后的几种情况(插入之前肯定满足红黑树)：

---

---

---

---

这样红黑树的插入操作的几种情况就已经分析完毕，那么如果给定一棵树，我们怎么判断是不是一棵红黑树？？这里，我们需要从红黑树的性质入手去一条一条检查。根节点是黑色结点，这一条很明显。主要是，红色结点不要连续和每条路径上的黑色结点的数量相同这两条性质的验证。
思路：对于判断是否有连续的红色结点这个比较好判断（每个结点和它的parent不同时为红色），对于每条路径的黑色结点的个数呢。我们可以采用任意给出一条路径的黑色结点的数目用来做基准，对于黑色结点的计数器k，我们采用传值的方式，因为，每一级的改变不需要也不能改变其上一级。
下边给出代码实现：
提供给外部的函数：

bool Blance()
    {
        if(_root == NULL)
        {
            return true;
        }
        int count = 0;//保存某一个路径上黑色结点的个数
        int k = 0;
        Node* cur = _root;
        while(cur)
        {
            if(cur->_col == BLACK)
            {
                ++count;
            }           
            cur = cur->_left;
        }
            return _Blance(_root,count,k);  
    }

内部调用函数：

//count表示任意一条路径上黑色结点的数目，用来做基准
    bool _Blance(Node* root,const int& count,int k)
    {
        if(root == NULL)
        {
            return k == count;
        }
        if(root->_col == BLACK)
        {
            ++k;
        }
        //相邻的红色结点
        if(root->_col == RED && root->_parent->_col == RED)
        {
            cout<<root->_key<<endl;
            return false;
        }
        return _Blance(root->_left,count,k) &&
                _Blance(root->_right,count,k);
    }

这样就可以判断一个树是不是红黑树。
对于红黑树的删除操作，同样是根据红黑树的性质进行旋转，调整颜色等等，由于情况多，这里不给出代码。
下边给出插入操作和判断平衡部分的所有实现代码：

#pragma once
#include<iostream>
using namespace std;
#include<stack>

enum COLOR
{
    RED,
    BLACK
};

template<typename K,typename V>
struct RBTreeNode
{

    K _key;
    V _value;

    RBTreeNode<K, V>* _parent;
    RBTreeNode<K, V>* _left;
    RBTreeNode<K, V>* _right;

    COLOR _col;

    RBTreeNode(const K& key,const V& value = 0)
        :_key(key)
        ,_value(value)
        ,_parent(NULL)
        ,_left(NULL)
        ,_right(NULL)
        ,_col(RED)
    {}
};
template<typename K,typename V>
class RBTree
{
    typedef RBTreeNode<K, V> Node;
public:
    RBTree()
        :_root(NULL)
    {}

    bool Insert(const K& key)
    {
        if (_root == NULL)
        {
            _root = new Node(key);
            _root->_col = BLACK;
            return true;
        }
        Node* cur = _root;
        Node* parent = NULL;
        while (cur)
        {
            if (cur->_key < key)
            {
                parent = cur;
                cur = cur->_right;
            }
            else if (cur->_key > key)
            {
                parent = cur;
                cur = cur->_left;
            }
            else//找到有相同的元素
                return false;
        }

        cur = new Node(key);
        //parent必不为NULL
        if (parent->_key < key)
            parent->_right = cur;
        else
            parent->_left = cur;
        cur->_parent = parent;
        //调整
        while (cur != _root && parent->_col == RED)
        {
            Node* grandFather = parent->_parent;//grandFather必不为空
            Node* uncle = NULL;
            if (parent == grandFather->_left)
            {
                uncle = grandFather->_right;
                //1.uncle存在且是红色
                if (uncle && uncle->_col == RED)
                {
                    parent->_col = BLACK;
                    uncle->_col = BLACK;
                    grandFather->_col = RED;
                    //向上调整
                    cur = grandFather;
                    parent = cur->_parent;
                }
                //2.uncle存在且是黑色
                //3.uncle不存在
                else
                {
                    if (cur == parent->_right)
                    {
                        _RotateL(parent);
                        swap(parent,cur);
                    }

                    _RotateR(grandFather);

                    //cur->_col = RED;
                    parent->_col = BLACK;
                    grandFather->_col = RED;

                    cur = parent;
                    parent = cur->_parent;
                }
            }

            else             //if (grandFather && parent == grandFather->_right)
            {
                uncle = grandFather->_left;
                if (uncle && uncle->_col == RED)
                {
                    parent->_col = BLACK;
                    uncle->_col = BLACK;
                    grandFather->_col = RED;
                    //向上调整
                    cur = grandFather;
                    parent = cur->_parent;
                }
                else
                {
                    if (cur == parent->_left)
                    {
                        _RotateR(parent);
                        swap(cur,parent);
                    }
                    _RotateL(grandFather);

                    //cur->_col = RED;
                    grandFather->_col = RED;
                    parent->_col = BLACK;

                    cur = parent;
                    parent = cur->_parent;
                }
            }
        }
        _root->_col = BLACK;
        return true;
    }
    void InOrderNonR()
    {
        if (_root == NULL)
        {
            cout << endl;
            return;
        }
        Node* cur = _root;
        stack<Node*> s;
        while (cur || !s.empty())
        {
            while (cur)
            {
                s.push(cur);
                cur = cur->_left;
            }
            Node* top = s.top();
            s.pop();
            cout << top->_key << " ";
            cur = top->_right;
        }
        cout << endl;
    }
    bool Blance()
    {
        if(_root == NULL)
        {
            return true;
        }
        int count = 0;//保存某一个路径上黑色结点的个数
        int k = 0;
        Node* cur = _root;
        while(cur)
        {
            if(cur->_col == BLACK)
            {
                ++count;
            }           
            cur = cur->_left;
        }
            return _Blance(_root,count,k);  
    }
protected:
    //count表示任意一条路径上黑色结点的数目，用来做基准
    bool _Blance(Node* root,const int& count,int k)
    {
        if(root == NULL)
        {
            return k == count;
        }
        if(root->_col == BLACK)
        {
            ++k;
        }
        //相邻的红色结点
        if(root->_col == RED && root->_parent->_col == RED)
        {
            cout<<root->_key<<endl;
            return false;
        }
        return _Blance(root->_left,count,k) &&
                _Blance(root->_right,count,k);
    }



    void _RotateL(Node* parent)
    {
        Node* subR = parent->_right;
        Node* subRL = subR->_left;
        Node* ppNode = parent->_parent;

        //连接parent和subRL
        parent->_right = subRL;
        if (subRL)
            subRL->_parent = parent;

        //连接parent和subR
        subR->_left = parent;
        parent->_parent = subR;

        //连接ppNode和subR
        if (ppNode == NULL)
        {
            _root = subR;
            _root->_parent = NULL;
        }
        else
        {
            if (parent == ppNode->_left)
                ppNode->_left = subR;
            else
                ppNode->_right = subR;
            subR->_parent = ppNode;
        }
    }
    void _RotateR(Node* parent)
    {
        Node* subL = parent->_left;
        Node* subLR = subL->_right;
        Node* ppNode = parent->_parent;
        //连接parent和subLR
        parent->_left = subLR;
        if (subLR)
            subLR->_parent = parent;
        //连接parent和subL
        subL->_right = parent ;
        parent->_parent = subL;

        if (ppNode == NULL)
        {
            _root = subL;
            _root->_parent = NULL;
        }
        else
        {
            if (parent == ppNode->_left)
                ppNode->_left = subL;
            else
                ppNode->_right = subL;
            subL->_parent = ppNode;
        }
    }
private:
    Node* _root;
};

关于红黑树，就简单整理到这里~~~