pezhzh的快乐寒假作业[2024/1/22]

最新推荐文章于 2024-08-10 20:38:44 发布

pezhzh

最新推荐文章于 2024-08-10 20:38:44 发布

阅读量941

点赞数 13

文章标签：算法

本文链接：https://blog.csdn.net/pezhzh/article/details/138826401

版权

这次的题目集只有两题！
耶 ↑
但是标签全是“数学”、“构造”！
欧 ↓

A - Koishi Loves Construction

洛谷：P3599；

两个Task，分别是要前缀和的 mod n 各项不相同与前缀积的 mod n 各项不相同；

一个个看吧！

Task 1：

看着官方的样例，我承认我确实试过倒序输出 n；

遗憾 0 分；

那就打个表看一下吧~

不难看出，1以外的奇数都无法完成；

而所有其他情况都只能将 n 放在第一个；
（因为要是将 n 放在其他地方就会导致 s [ n - 1 ] % n == s [ n ] % n）
毕竟 n % n = 0 嘛；

在然后可以找到规律，偶数位为 1,3,5,7 奇数位为倒序的 2,4,6,8；

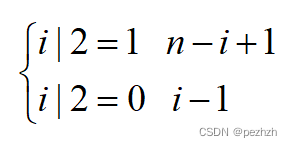
通项公式 ↑

试提交后成功拿到 50 分；

Task 2：

有了 T1 的经验，再来看看 T2 有没有什么规律吧？

先理性分析，因为前缀和是不能有 [ L , R ] 之和 mod n 为 0，

那前缀积同理就不能有 [ L , R ] 之积 mod n 为 0；

且不能有 [ L , R ] 之积 mod n 为 1；

前缀和第一个必须是 n；

前缀积第一个必须是 1，最后必须是 n；

因为几乎对于所有的合数，都有 p * q = n ( p != q ) ，所以不合法；

唯一的例外是 4，因为 4 = 2 * 2，不存在 ( p != q )；

那么，答案就只有一个了！(误，答案不唯一，只是有了一种而已)

使前缀积 mod n 为 1 ~ n；

#include <bits/stdc++.h>
#define FOR_(I, S, N) for (int I=(S), END=(N); I<=END; I++)
using namespace std;
typedef long long ll;
const int C = 1e5 + 10;

int x, t, n, cnt = 0;
int p[C], h[C];

void prime()
{
	for(int i = 2; i < C; i ++)
	{
		if(!p[i])
		{
			h[cnt ++] = i;
			for(int j = 2; j * i < C; j ++)
				p[j * i] = 1;
		}
	}
}

ll Pow(ll a, int x){
	ll res = 1;
	for(; x; a = a * a % n, x >>= 1)
		if(x & 1) res = res * a % n;
	return res;
}

int main()
{
	cin >> x >> t;
	if(x == 1)
	{
		while(t --)
		{
			cin >> n;
			if(n == 1) cout << "2 1" << endl;
			else if(n % 2) cout << 0 << endl;
			else
			{
				cout << 2;
				for(int i = 1; i <= n; i ++) cout << ' ' << (i % 2 ? n - i + 1 : i - 1);
				puts("");
			}
		}
	}
	else
	{
		prime();
		while(t --)
		{
			cin >> n;
			if(n == 1) cout << "2 1" << endl;
			else if(n == 4) cout << "2 1 3 2 4" << endl;
			else
			{
				if(p[n]) cout << 0 << endl;
				else
				{
					cout << 2;
					ll tmp = 1, sum = 1;
					for(int i = 1; i < n; i ++){
						cout << ' ' << tmp;
						tmp = Pow(sum, n - 2) * (i + 1) % n;
						sum ++;
					}
					cout << ' ' << n << endl;
				}
			}
		}
	}
}

AC；

B - 伤痕

洛谷：P5441；

这里必须先指明，作者无法做出同难度同类型的题；

所以其实这是一个别人的题解的转述（

首先这是一道数学题，咱们以数学方法来分析：

要求国王选择的方案数最大，那便是要求能互相直达的四点组合足够多；

同理，则是要使无法互相直达的四点组合最小；

四点组合到底有多少呢

在 n 个点里取 4 个点的不同组合自然是 $C_{n}^{4}$ ；

而奇数点的单项向边数便是 $\frac{n*(n-1)}{2}-n=\frac{n*(n-3)}{2}$ ，其中前一项是总边数，第二项是双向边的数量；

无法互相直达的四点组合分类

四点直接的路径大致长这样

1.有个点进不去

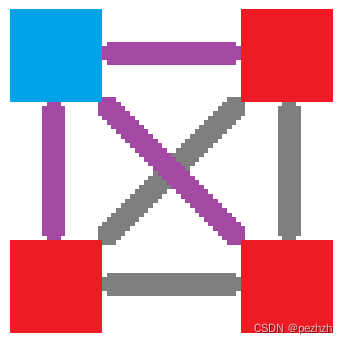
2.有个点出不来

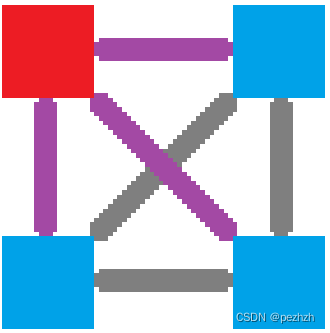
3.有两个点与另两个点只能单向传送

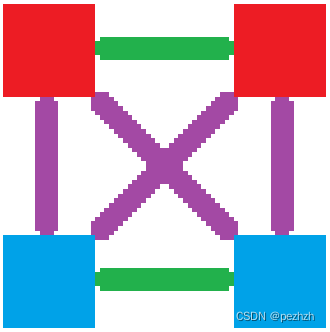
在上述图中，蓝色代表出得去的点，红色代表进得来的点，紫色代表单向路，绿色代表双向路；

该三种情况囊括了所有的无法互相直达的四点集合类型；

减少他们出现的方法我们一个个讨论；

第一种情况，

我们设城市 $i$ 有 $S_{i}$ 条向外的单行道，如果 $S_{i}\geqslant 3$ 那么它就可以和其中三个城市组成类型一，所以对于城市 $i$ 的类型一的总数有 $C_{S_{i}}^{3}$ 个；

对于所有城市则有： $\sum_{i=1}^{n}C_{S_{i}}^{3}$

而且我们已知单向路的总数为 $\frac{n*(n-3)}{2}$

得出： $\sum_{i=1}^{n}S_{i}=\frac{n*(n-3)}{2}$

要使得类型一总数最小，就得使得 $S_{i}$ 之间的差最小，因此我们让所有 $S_{i}$ 相等，也即取值 $\frac{n-3}{2}$

那么第一类的总数为： $n*C_{\frac{n-3}{2}}^{3}=\frac{n(n-3)(n-5)(n-7)}{48}$

其他情况，

有一种构造能使得第二种与第三种情况减少至0；

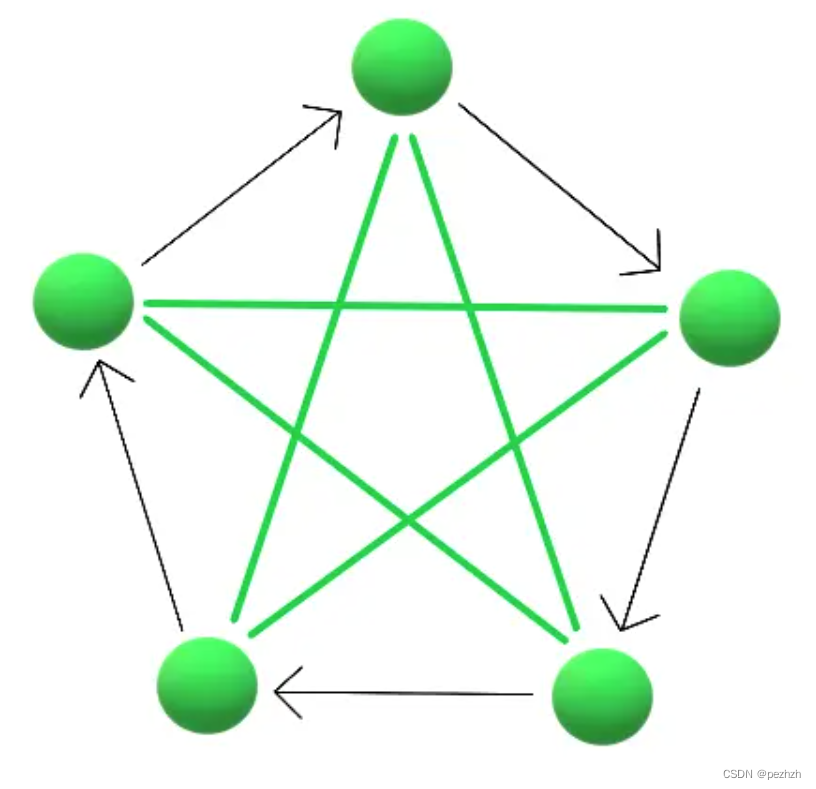
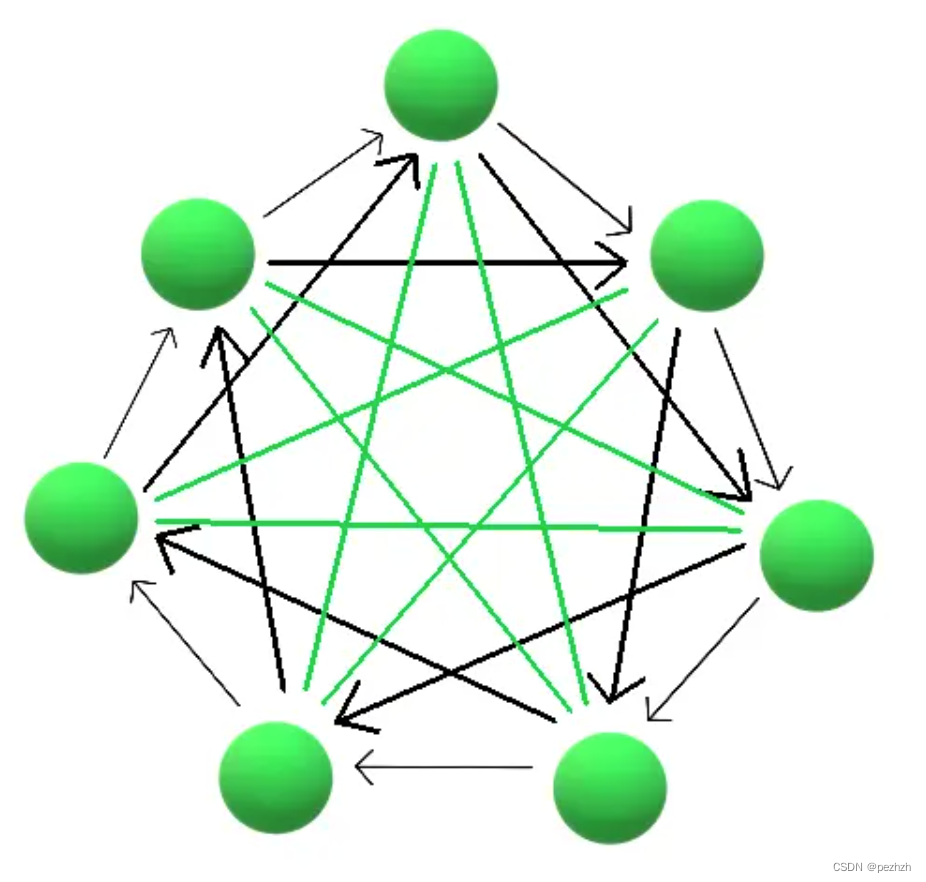以上两幅图可以看出，除了最长对角线的两个点需要双向路以外，其余单向路都是顺时针指向下一个点，那么每无法互达的四个点都是类型一；

n个点中每个点都有n - 1条边，而减去了两条最长对角线的双向路之后，单向路的数量就是 $\frac{n-3}{2}$

与上一段不谋而合；

可以直达的四点

那么就可以相减计算结果了！

$C_{n}^{4}-n*C_{\frac{n-3}{2}}^{3} = \frac{n(n-1)(n-2)(n-3)}{24}-\frac{n(n-3)(n-5)(n-7)}{48}=\frac{n(n-3)(n^{2}-6n-31)}{48}$

#include <bits/stdc++.h>
#define FOR_(I, S, N) for (int I=(S), END=(N); I<=END; I++)
using namespace std;
typedef long long ll;
const int C = 100;

int n;
int c[C][C];

int main()
{
	cin >> n;
	if(n == 1)
	{
		cout << "0\n0";
		return 0;
	}
	cout << n * (n - 3) * (n * n + 6 * n - 31) / 48 << endl;
	FOR_(i, 1, n)
	FOR_(j, i + 1, i + (n + 1) / 2)
	c[i][(j - 1) % n + 1] = 1;
	FOR_(i, 1, n)
	{
		FOR_(j, 1, n)
		cout << c[i][j] << ' ';
		puts("");
	}
}