算法导论 第二十二章 基本的图算法

最新推荐文章于 2023-11-16 20:42:39 发布
最新推荐文章于 2023-11-16 20:42:39 发布
阅读量551 收藏 2
点赞数 1
分类专栏： 算法笔记
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/pokeyode/article/details/53509895
版权

22.1图的表示

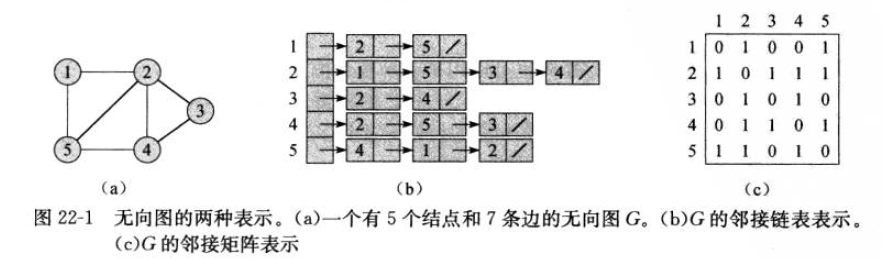
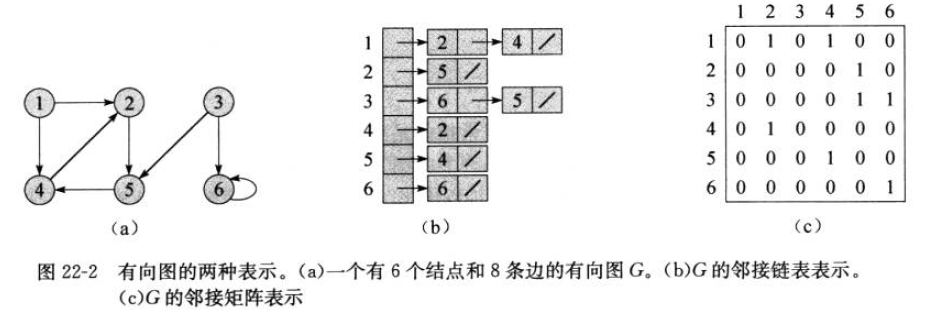
图结构G(V,E)由顶点V和边E的集合组成，主要有邻接链表表示和邻接矩阵表示，两者的差别如下所示：



若为节点添加属性则可以通过改变节点自身的值，或者为节点添加属性或在节点中增加新的指针的方式来实现。权重也是属性的一种。

22.2 广度优先搜索

对于给定一个图中的原点，从原点出发按照到原点的距离来遍历所有的连通节点称为广度优先搜索。连接链表的算法广度优先搜索算法如下：

def ENQUEUE(Q, s):
    Q.append(s)

def DEQUEUE(Q):
    r = Q.pop(0)
    return r

WHITE, GRAY, BLACK = (0, 1, 2)

class Vertex:
    def __init__(self, u):
        self.value = u
        self.color = WHITE
        self.d = float("inf")
        self.pi = None

class Edge:
    def __init__(self, u, v):
        self.fromV = u
        self.toV = v

class EdgeList:
    def __init__(self, v):
        self.vertex = v
        self.connectedV = []

class Graph:
    def __init__(self):
        self.vertexs = {}

def CONNECT(u, v):
    return Edge(u, v)

def INITGRAPH(G, edges):
    for e in edges:
        if not e.fromV.value in G.vertexs:
            G.vertexs[e.fromV.value] = EdgeList(e.fromV)
        if not e.toV.value in G.vertexs:
            G.vertexs[e.toV.value] = EdgeList(e.toV)

        G.vertexs[e.fromV.value].connectedV.append(e.toV)
        G.vertexs[e.toV.value].connectedV.append(e.fromV)

def PRINTLIST(el):
    print(el.vertex.value, ":")
    for v in el.connectedV:
        print(v.value)

def PRINTGRAPH(G):
    for v in G.vertexs:
        PRINTLIST(G.vertexs[v])
        print("-----")

def BFS(G, s):
    for v in G.vertexs:
        if v != s.value:
            G.vertexs[v].vertex.color = WHITE
            G.vertexs[v].vertex.d = float("inf")
            G.vertexs[v].vertex.pi = None

    s.color = GRAY
    s.d = 0
    s.pi = None

    Q = []
    ENQUEUE(Q, s)
    while len(Q) != 0:
        u = DEQUEUE(Q)
        for v in G.vertexs[u.value].connectedV:
            if v.color == WHITE:
                v.color = GRAY
                v.d = u.d + 1
                v.pi = u
                ENQUEUE(Q, v)
        u.color = BLACK
        print(u.value, u.d)

def PRINT_PATH(G, s, v):
    if v == s:
        print(s.value)
    elif v.pi == None:
        print("no path from ", s.value, " to ", v.value, "exists")
    else:
        PRINT_PATH(G, s, v.pi)
        print(v.value)


if __name__ == "__main__":
    r = Vertex('r')
    s = Vertex('s')
    t = Vertex('t')
    u = Vertex('u')
    v = Vertex('v')
    w = Vertex('w')
    x = Vertex('x')
    y = Vertex('y')

    edges = []
    edges.append(CONNECT(r, s))
    edges.append(CONNECT(r, v))
    edges.append(CONNECT(s, w))
    edges.append(CONNECT(w, t))
    edges.append(CONNECT(w, x))
    edges.append(CONNECT(t, x))
    edges.append(CONNECT(t, u))
    edges.append(CONNECT(x, u))
    edges.append(CONNECT(x, y))
    edges.append(CONNECT(u, y))

    G = Graph()
    INITGRAPH(G, edges)
    PRINTGRAPH(G)

    print("**************")
    BFS(G, s)
    print("++++++++++++++")
    PRINT_PATH(G, s, y)
我们采用循环不变式：queue中保存的节点到原点的距离为最短距离。采用书上的证明其正确性，概括如下：因为广度遍历的先将d小的加入queue中，当节点第一次被发现时其pi的距离+1即为最短距离。

22.3 深度优先搜索

类似与广度优先搜索，深度优先搜索算法沿着连接的边一路查找直到所有的连接点都已经发现在原路返回查找所有节点，实现如下：

def ENQUEUE(Q, s):
    Q.append(s)

def DEQUEUE(Q):
    r = Q.pop(0)
    return r

WHITE, GRAY, BLACK = (0, 1, 2)

class Vertex:
    def __init__(self, u):
        self.value = u
        self.color = WHITE
        self.d = float("inf")
        self.f = float("inf")
        self.pi = None

class Edge:
    def __init__(self, u, v):
        self.fromV = u
        self.toV = v

class EdgeList:
    def __init__(self, v):
        self.vertex = v
        self.connectedV = []

class Graph:
    def __init__(self):
        self.vertexs = {}

def CONNECT(u, v):
    return Edge(u, v)

def INITGRAPH(G, edges):
    for e in edges:
        if not e.fromV.value in G.vertexs:
            G.vertexs[e.fromV.value] = EdgeList(e.fromV)
        if not e.toV.value in G.vertexs:
            G.vertexs[e.toV.value] = EdgeList(e.toV)

        G.vertexs[e.fromV.value].connectedV.append(e.toV)
        #G.vertexs[e.toV.value].connectedV.append(e.fromV)

def PRINTLIST(el):
    print(el.vertex.value, ":")
    for v in el.connectedV:
        print(v.value)

def PRINTGRAPH(G):
    for v in G.vertexs:
        PRINTLIST(G.vertexs[v])
        print("-----")

global time
time = 0
def DFS(G):
    for u in sorted(G.vertexs.keys()):
        G.vertexs[u].vertex.color = WHITE
        G.vertexs[u].vertex.pi = None
    global time
    time = 0
    for u in sorted(G.vertexs.keys()):
        if G.vertexs[u].vertex.color == WHITE:
            DFS_VISIT(G, G.vertexs[u].vertex)

def DFS_VISIT(G, u):
    global time
    time = time + 1
    u.d = time
    u.color = GRAY
    for v in G.vertexs[u.value].connectedV:
        if v.color == WHITE:
            v.pi = u
            DFS_VISIT(G, v)
    u.color = BLACK
    time = time + 1
    u.f = time
    print(u.value, u.d, u.f)

if __name__ == "__main__":
    u = Vertex('u')
    v = Vertex('v')
    w = Vertex('w')
    x = Vertex('x')
    y = Vertex('y')
    z = Vertex('z')

    edges = []
    edges.append(CONNECT(u, v))
    edges.append(CONNECT(u, x))
    edges.append(CONNECT(v, y))
    edges.append(CONNECT(w, y))
    edges.append(CONNECT(w, z))
    edges.append(CONNECT(x, v))
    edges.append(CONNECT(y, x))
    edges.append(CONNECT(z, z))

    G = Graph()
    INITGRAPH(G, edges)
    PRINTGRAPH(G)

    print("===========")
    DFS(G)

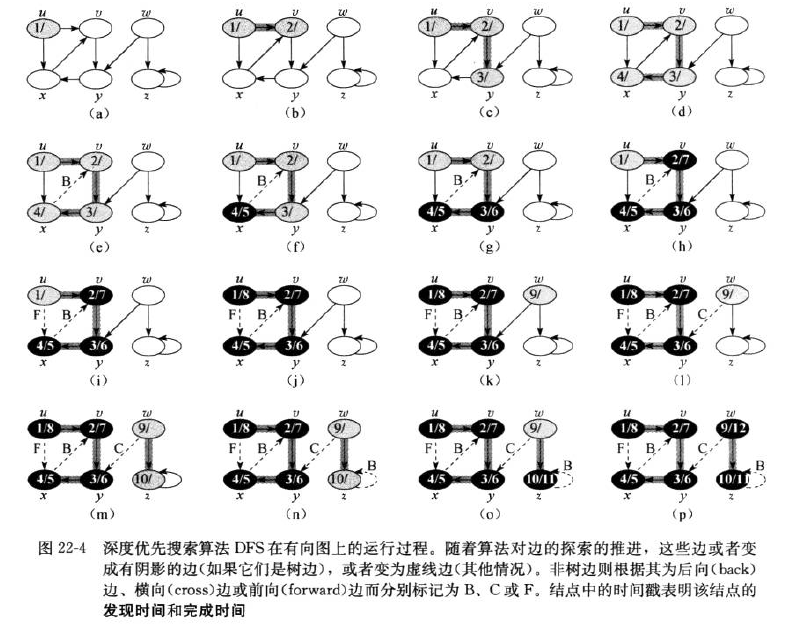
根据检索的边的连接点的不同，可以将边分为如下类型：

而且易证深度优先搜索有如下性质：

22.4 拓扑排序

拓扑排序就是无向环图的深度优先遍历中u.f值的由大到小的线性排序。

def ENQUEUE(Q, s):
    Q.append(s)

def DEQUEUE(Q):
    r = Q.pop(0)
    return r

WHITE, GRAY, BLACK = (0, 1, 2)

class Vertex:
    def __init__(self, u):
        self.value = u
        self.color = WHITE
        self.d = float("inf")
        self.f = float("inf")
        self.pi = None

class Edge:
    def __init__(self, u, v):
        self.fromV = u
        self.toV = v

class EdgeList:
    def __init__(self, v):
        self.vertex = v
        self.connectedV = []

class Graph:
    def __init__(self):
        self.vertexs = {}

def CONNECT(u, v):
    return Edge(u, v)

def INITGRAPH(G, edges):
    for e in edges:
        if not e.fromV.value in G.vertexs:
            G.vertexs[e.fromV.value] = EdgeList(e.fromV)
        if not e.toV.value in G.vertexs:
            G.vertexs[e.toV.value] = EdgeList(e.toV)

        G.vertexs[e.fromV.value].connectedV.append(e.toV)
        #G.vertexs[e.toV.value].connectedV.append(e.fromV)

def PRINTLIST(el):
    print(el.vertex.value, ":")
    for v in el.connectedV:
        print(v.value)

def PRINTGRAPH(G):
    for v in G.vertexs:
        PRINTLIST(G.vertexs[v])
        print("-----")

global time
time = 0
def DFS(G, TG):
    for u in sorted(G.vertexs.keys()):
        G.vertexs[u].vertex.color = WHITE
        G.vertexs[u].vertex.pi = None
    global time
    time = 0
    for u in sorted(G.vertexs.keys()):
        if G.vertexs[u].vertex.color == WHITE:
            DFS_VISIT(G, G.vertexs[u].vertex, TG)

def DFS_VISIT(G, u, TG):
    global time
    time = time + 1
    u.d = time
    u.color = GRAY
    for v in G.vertexs[u.value].connectedV:
        if v.color == WHITE:
            v.pi = u
            DFS_VISIT(G, v, TG)
    u.color = BLACK
    time = time + 1
    u.f = time
    TG.append(u)
    #print(u.value, u.d, u.f)

def TOPOLOGICAL_SORT(G):
    TG = []
    DFS(G, TG)
    return TG

if __name__ == "__main__":
    a = Vertex('a')
    b = Vertex('b')
    c = Vertex('c')
    d = Vertex('d')
    e = Vertex('e')
    f = Vertex('f')
    g = Vertex('g')
    h = Vertex('h')
    i = Vertex('i')

    edges = []
    edges.append(CONNECT(a, b))
    edges.append(CONNECT(a, d))
    edges.append(CONNECT(b, c))
    edges.append(CONNECT(d, c))
    edges.append(CONNECT(e, e))
    edges.append(CONNECT(f, g))
    edges.append(CONNECT(f, i))
    edges.append(CONNECT(g, i))
    edges.append(CONNECT(g, d))
    edges.append(CONNECT(h, i))



    G = Graph()
    INITGRAPH(G, edges)
    PRINTGRAPH(G)

    print("===========")
    TG = TOPOLOGICAL_SORT(G)
    for u in TG:
        print(u.value, u.d, u.f)

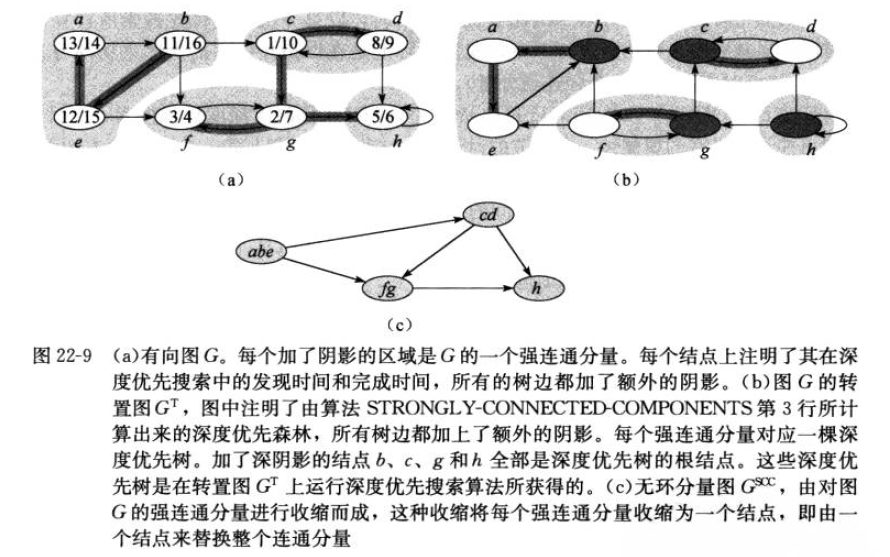
22.5 强连通分量
强连通分量其实就是环，把图G中的环归并到一起，就能将有环图变为无环图，无环图的许多算法可以被应用。如下图：

通过如下代码实现：

def ENQUEUE(Q, s):
    Q.append(s)

def DEQUEUE(Q):
    r = Q.pop(0)
    return r

WHITE, GRAY, BLACK = (0, 1, 2)

class Vertex:
    def __init__(self, u):
        self.value = u
        self.color = WHITE
        self.d = float("inf")
        self.f = float("inf")
        self.pi = None
        self.k = 0

class Edge:
    def __init__(self, u, v):
        self.fromV = u
        self.toV = v

class EdgeList:
    def __init__(self, v):
        self.vertex = v
        self.connectedV = []

class Graph:
    def __init__(self):
        self.vertexs = {}

def CONNECT(u, v):
    return Edge(u, v)

def INITGRAPH(G, edges):
    for e in edges:
        if not e.fromV.value in G.vertexs:
            G.vertexs[e.fromV.value] = EdgeList(e.fromV)
        if not e.toV.value in G.vertexs:
            G.vertexs[e.toV.value] = EdgeList(e.toV)

        G.vertexs[e.fromV.value].connectedV.append(e.toV)
        #G.vertexs[e.toV.value].connectedV.append(e.fromV)

def PRINTLIST(el):
    print(el.vertex.value, ":")
    for v in el.connectedV:
        print(v.value)

def PRINTGRAPH(G):
    for v in G.vertexs:
        PRINTLIST(G.vertexs[v])
        print("-----")

global time
time = 0
def DFS(G, TG, keys):
    for u in keys:
        G.vertexs[u].vertex.color = WHITE
        G.vertexs[u].vertex.pi = None
    global time
    time = 0
    k = 1
    for u in sorted(G.vertexs.keys()):
        if G.vertexs[u].vertex.color == WHITE:
            DFS_VISIT(G, G.vertexs[u].vertex, TG, k)
            k = k + 1

def DFS_VISIT(G, u, TG, k):
    global time
    time = time + 1
    u.d = time
    u.color = GRAY
    for v in G.vertexs[u.value].connectedV:
        if v.color == WHITE:
            v.pi = u
            DFS_VISIT(G, v, TG, k)
    u.color = BLACK
    time = time + 1
    u.f = time
    u.k = k
    TG.append(u)
    #print(u.value, u.d, u.f)

def TOPOLOGICAL_SORT(G, keys):
    TSG = []
    DFS(G, TSG, keys)
    return TSG

def TRANSPOSE(G):
    edges = []
    for k in G.vertexs.keys():
        u = G.vertexs[k].vertex
        for v in G.vertexs[u.value].connectedV:
            edges.append(CONNECT(v, u))

    GT = Graph()
    INITGRAPH(GT, edges)
    return GT

def STRONGLY_CONNECTED_COMPONENTS(G, k):
    GT = TRANSPOSE(G)

    tsg = TOPOLOGICAL_SORT(G, k)
    keys = []
    for u in tsg:
        keys.insert(0,u.value)
        print(u.value)

    gtts = []
    DFS(GT, gtts, keys)
    print("------------")
    k = 0
    for u in gtts:
        if u.k != k:
            print("|")
            k = u.k
        print(u.value)

if __name__ == "__main__":
    a = Vertex('a')
    b = Vertex('b')
    c = Vertex('c')
    d = Vertex('d')
    e = Vertex('e')
    f = Vertex('f')
    g = Vertex('g')
    h = Vertex('h')

    edges = []
    edges.append(CONNECT(a, b))
    edges.append(CONNECT(b, c))
    edges.append(CONNECT(b, e))
    edges.append(CONNECT(b, f))
    edges.append(CONNECT(c, d))
    edges.append(CONNECT(c, g))
    edges.append(CONNECT(d, c))
    edges.append(CONNECT(d, h))
    
    edges.append(CONNECT(e, a))
    edges.append(CONNECT(e, f))
    edges.append(CONNECT(f, g))
    edges.append(CONNECT(g, f))
    edges.append(CONNECT(g, h))
    edges.append(CONNECT(h, h))



    G = Graph()
    INITGRAPH(G, edges)
    PRINTGRAPH(G)

    #STRONGLY_CONNECTED_COMPONENTS(G, ['c', 'g','f','h','d','b','e','a'])
    keys = sorted(G.vertexs.keys())
    print(keys)
    STRONGLY_CONNECTED_COMPONENTS(G, keys)



习题解答

pokeyode
关注
  • 1
    点赞
  • 踩
  • 2
    收藏
    觉得还不错? 一键收藏
  • 0
    评论
专栏目录
算法导论第二十二章习题解答
01-09
能用代码表示的都用代码表示，不能表示的写出思路，思路都没写的就是我也做不出来
《算法导论》第22章——基本的图算法
T的博客
11-09 1584
  虽然写这个博客主要目的是为了给我自己做一个思路记忆录，但是如果你恰好点了进来，那么先对你说一声欢迎。我并不是什么大触，只是一个菜菜的学生，如果您发现了什么错误或者您对于某些地方有更好的意见，非常欢迎您的斧正！ 图的搜索指的是系统化地跟随图中的边来访问图中的每个结点。 22.1图的表示 权重图：图中的每条边都带有一个相关的权重的图。 该权重值通常由一个w：E→R的权重函数给出。 例如，...
算法导论——基本的图算法
weixin_34258078的博客
08-06 196
　　对于图G=(V,E)，V代表点，E代表边。图有两种标准的表示方法：邻接矩阵法和邻接链表法。 　　邻接链表法适合表示边的条数少的稀疏图，可以节约存储空间。对于有向图G来说，边(u,v)一定会出现在链表Adj[u]中，因此，所有链表的长度之和一定等于|E|。对于无向图来说，边(u,v)会同时出现在Adj[u]和Adj[v]中，因此所有链表的长度之和一...
算法导论之图算法
liu_matthew的博客
02-19 830
算法导论之图算法标签（空格分隔）： 学习笔记一、基本图算法1.1 图的表示对于图G = （V,E）中，V代表图的顶点，E代表顶点之间的关系，也就是我们通常说的边。按照边的特性我们可以将图分为有向图或者无向图。但是所有的无向图中的边我们可以用两条互指的有向边进行代替，将无向图转换为有向图，所以这里所有的算法都针对有向图。1.1.1 邻接链表邻接链表表示方法由一个包含|V|条链表的数组Adj所构成，每个
算法导论【图算法】—最小生成树、最短路径、最大流算法总结
我们都是被分成两半的人，一边热爱生活，一边憎恨生活。面对生活，我们总是在矛盾的两端摇摆，在反复的矛盾和犹豫中，一边踉跄前行，一边重振旗鼓。我渴望改变，渴望变得更好，渴望找到出口……就像一个溺水人的挣扎，就像一个救生圈。我是一个矛盾集合体，想要变得快乐，但是
02-09 1270
Dijkstra算法 - 顶点为V，边为E的图 1. 对每条边仅松弛1次 2. 边权不可为负 3. 运行过程维护一组结点集合S 4. 使用贪心策略，每次选择集合V-S中最“近”的结点加入集合S 5. 利用结点编号维持最小优先队列,时间复杂度为：
算法导论-第三版(中文).rar
09-18
第二十二章 基本的图算法（Elementary Graph Algorithms） 第二十三章 最小生成树（Minimum Spanning Trees） 第二十四章单源最短路径（Single-Source Shortest Paths） 第二十五章 全对的最短路径（All-Pairs ...
算法导论（中文 第二版）答案
03-08
　第二十二章 基本的图算法（Elementary Graph Algorithms） 　第二十三章 最小生成树（Minimum Spanning Trees） 　第二十四章 单源最短路径（Single-Source Shortest Paths） 　第二十五章 全对的最短路径（All...
算法导论（第2版）参考答案
03-08
　第二十二章 基本的图算法（Elementary Graph Algorithms） 　第二十三章 最小生成树（Minimum Spanning Trees） 　第二十四章 单源最短路径（Single-Source Shortest Paths） 　第二十五章 全对的最短路径（All-...
算法导论 第二版
10-14
第22章 图的基本算法 第23章 最小生成树 第24章 单源最短路径 第25章 每对项点间的最短路径 第26章 最大流 第七部分 算法研究问题选编 引言 第27章 排序网络 第28章 矩阵运算 第29章 线性规划 第30章 多项式与快速...
算法导论学习—— 22章 基本的图算法
weixin_42078418的博客
03-29 166
算法导论学习—— 22章 基本的图算法图的表示广度优先搜索深度优先搜索拓扑排序强连通分量 图的表示 邻接表表示方法：经常用于表示稀疏图(边数远小于节点数平方） 邻接矩阵表示方法：可以用于表示稠密图（边数接近节点数平方） 广度优先搜索 采用队列操作，不断取出队首节点，搜索队首节点所邻未访问过的节点入队。记录搜索前驱可得到广度优先树，包含源节点到任意节点的最短路径。 深度优先搜索 采用栈操作，将栈...
算法导论22章课后习题答案
01-26
最近在研习算法导论，发现课后习题的精彩程度甚至不亚于正文，对于算法导论的爱好者而言，这是一份不错的参考资料
《算法导论3rd第二十二章》基础的图算法
懒猫的脚印
12-16 811
算法导论， 第二十二章，基础图算法
算法导论之图算法--图的基本概念
xueyuxueyuxueyu的博客
04-13 3405
是数据结构和算法学中最强大的框架之一（或许没有之一）。用途：1、用来表现所有类型的结构或系统2、交通网络3、通信网络4、下棋游戏5、最优流程6、任务分配7、人际交互网络。。。。。。下面首先介绍一下图论的基本概念，对其有基本了解之后再在实践中加深理解。图是将各种模型抽象成一些顶点，这些顶点之间可以通过图的边实现连接，即vretex和edge，如下图所示圆圈中的顶点和黑色的边：一、顶点电路图中电路元件...
算法导论（七）之图算法
yin__ren的博客
10-26 1087
1. 基本图算法 1. 广度优先搜索(BFS) 从临近源顶点s最近的顶点开始，通过对图G的边的探索发现从源顶点s能够抵达的每个顶点 1. 伪代码 BFS(G,s) for each vertex u 属于 G.V - {S} u.color = WHITE u.d = 无穷 u.pi = NIL s.color = GRAY s.d = 0 s.pi = NIL Q = ...
算法导论--图算法Part2
张丰的博客
01-19 484
图算法
《算法导论》第六部分---图算法
weixin_34415923的博客
06-23 88
简要的做一些记录，还有一些没看懂的地方先标记着以后再重新回过头来看。 22.1          图的表示    图的两种表示方法：                           1、邻接表                                     优点：邻接表表示法稍作修改，就能支持其他多种图的变体，因而有很强的适应性。                       ...
基本图论算法--《算法导论》
taotao 的大学墓志
08-23 7047
广度优先搜索（BFS）算法描述对于一个给定的图G(V,E)G (V,E) 和一个源节点SS BFS能遍历所有从SS出发能到达的节点，并计算SS 能到达每一个节点的距离（最少的边数），并生成一可广度优先搜索树。代码说明u.pu.p uu的前驱结点 u.du.d uu到SS的距离 u.coloru.color uu的状态，WHITE 未被搜索到，GRAY正在被发现，BLACK以搜索结束 QQ 队列
算法导论 第22章 基本的图算法 22.1 图的表示 习题解答
最新发布
CrystalLuo0827的博客
11-16 375
这是因为对于每个节点v，对其邻接链表中的每个邻接节点u，以及u的邻接链表中的每个节点w，都会执行一次操作，总的时间复杂度是边数和节点数的乘积。对于邻接链表表示的有向图，计算每个节点的出度需要遍历图中的每个节点，然后对于每个节点，遍历其邻接链表，统计邻接节点的数量即为该节点的出度。因此，出度的计算时间复杂度为O(V + E)，其中V是节点的数量，E是边的数量。对于有向图的入度，需要对图中的每个节点进行遍历，然后再对每个节点的邻接链表进行遍历，统计指向该节点的边的数量即为该节点的入度。
算法导论23章算法导论23章最小生成树习题
10-19
算法导论第23章主要讲述了最小生成树的相关算法，其中包括Kruskal算法和Prim算法。Kruskal算法是一种基于贪心策略的算法，它通过对边进行排序，然后依次加入边来构建最小生成树。而Prim算法则是一种基于节点的算法，...

“相关推荐”对你有帮助么？

  • 非常没帮助
  • 没帮助
  • 一般
  • 有帮助
  • 非常有帮助
提交
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值