IEEE 浮点数 规格化

IEEE念作"eye-triple-ee"

定义

IEEE浮点标准用 $V=(-1{)}^s\times M\times 2^E$ 的形式来表示一个数

• 符号(sign): $s$ 正负，对于数值0的符号位解释作特殊情况处理
• 尾数(significand) $M$是一个二进制小数，它的范围是$1\sim 2-\epsilon$，或者$0\sim 1-\epsilon$
• 阶码(exponent) $E$的作用是对浮点数加权，这个权重是2的$E$次幂（可能是负数）。

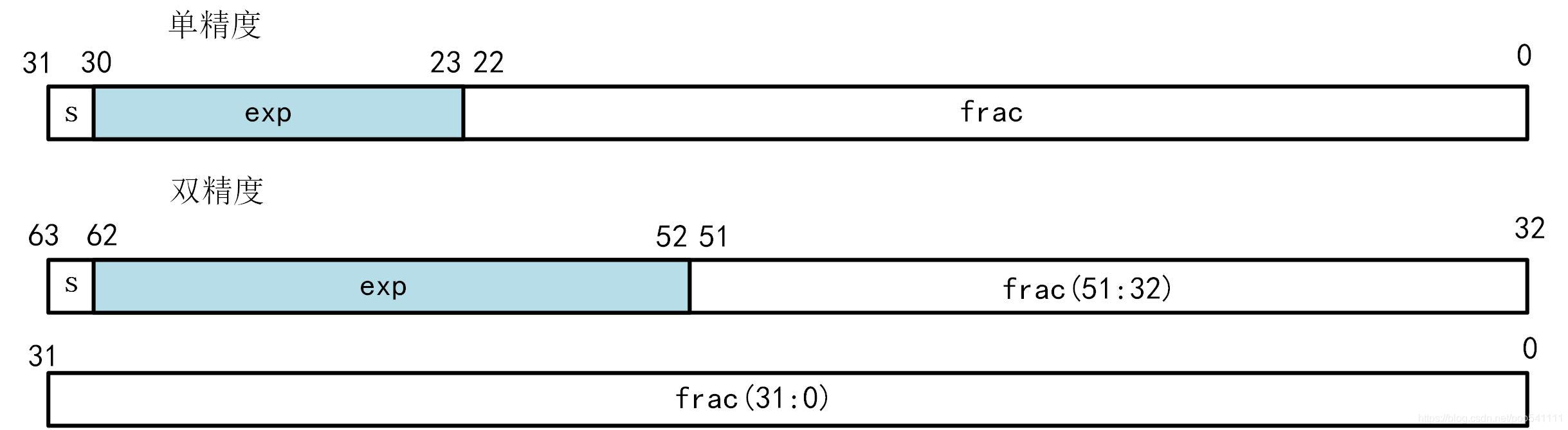
将浮点数的位表示划分为三个字段，分别对这些值进行编码：

• 一个单独的符号位 $s$ 直接编码符号 $s$
• $k$位的阶码字段 $\text{exp=}{e}_{k-1}...e_1{e}_0$ 编码阶码 $E$
• $n$位小数字段 $\text{frac=}{f}_{n-1}...f_1{f}_0$ 编码尾数 $M$，但是编码出来的值也依赖于阶码字段的值是否等于0

情况1:规格化的值

 这是最普遍的情况。当exp的位模式既不全为0(数值0)，也不全为1(单精度数值为255，双精度数值为2047)时，都属于这类情况。在这种情况中，阶码字段被解释为以偏置(biased)形式表示的有符号整数。也就是说，阶码的值是$E=e-Bias$，其中 $e$ 是无符号数，其位表示为 $e_{k-1}\dots e_1{e}_0$，而 $Bias$ 是一个等于 $2^{k-1}-1$ (单精度是127，双精度是1023)的偏置值。由此产生指数的取值范围，对于单精度是 $-126～＋127$，而对于双精度是 $-1022～＋1023$。
 小数字段frac被解释为描述小数值$f$，其中 $0\le f<1$，其二进制表示为 $0.f_{n-1}\dots f_1{f}_0$ ，也就是二进制小数点在最高有效位的左边。尾数定义为 $M=1十f$ 。有时,这种方式也叫做隐含的以1开头的(implied leading 1)表示，因为我们可以把 $M$看成一个二进制表达式为 $1.f_{n-1}{f}_{n-2}\dots f_0$ 的数字。既然我们总是能够调整阶码 $E$，使得尾数 $M$ 在范围$1\le M<2$ 之中(假设没有溢出)，那么这种表示方法是一种轻松获得一个额外精度位的技巧。既然第一位总是等于1,那么我们就不需要显式地表示它。

情况2:非规格化的值

 当阶码域为全0时，所表示的数是非规格化形式。在这种情况下，阶码值是 $E=1-Bias$,而尾数的值是$M=f$,也就是小数字段的值，不包含隐含的开头的1。
 非规格化数有两个用途。首先，它们提供了一种表示数值0的方法，因为使用规格化数,我们必须总是使 $M\ge 1$，因此我们就不能表示0。实际上,+0.0的浮点表示的位模式为全0：符号位是0，阶码字段全为0(表明是一个非规格化值)而小数域也全为0,这就得到$M=f=0$。令人奇怪的是，当符号位为1，而其他域全为0时，我们得到值-0.0。根据IEEE的浮点格式，值+0.0和-0.0在某些方面被认为是不同的，而在其他方面是相同的。
 非规格化数的另外一个功能是表示那些非常接近于0.0的数。它们提供了一种属性，称为逐渐下溢(gradual underflow)，其中，可能的数值分布均匀地接近于0.0。

情况3:特殊值

 最后一类数值是当指阶码全为1的时候出现的。当小数域全为0时，得到的值表示无穷，当s=0时是 $+\infty$，或者当s=1时是 $-\infty$ 。当我们把两个非常大的数相乘，或者除以零时，无穷能够表示溢出的结果。当小数域为非零时，结果值被称为“NaN”,即“不是一个数(Not a Number)”的缩写。一些运算的结果不能是实数或无穷，就会返回这样的NaN值，比如当计算$\sqrt{-1}$或$\infty -\infty$时。在某些应用中，表示未初始化的数据时,它们也很有用处。

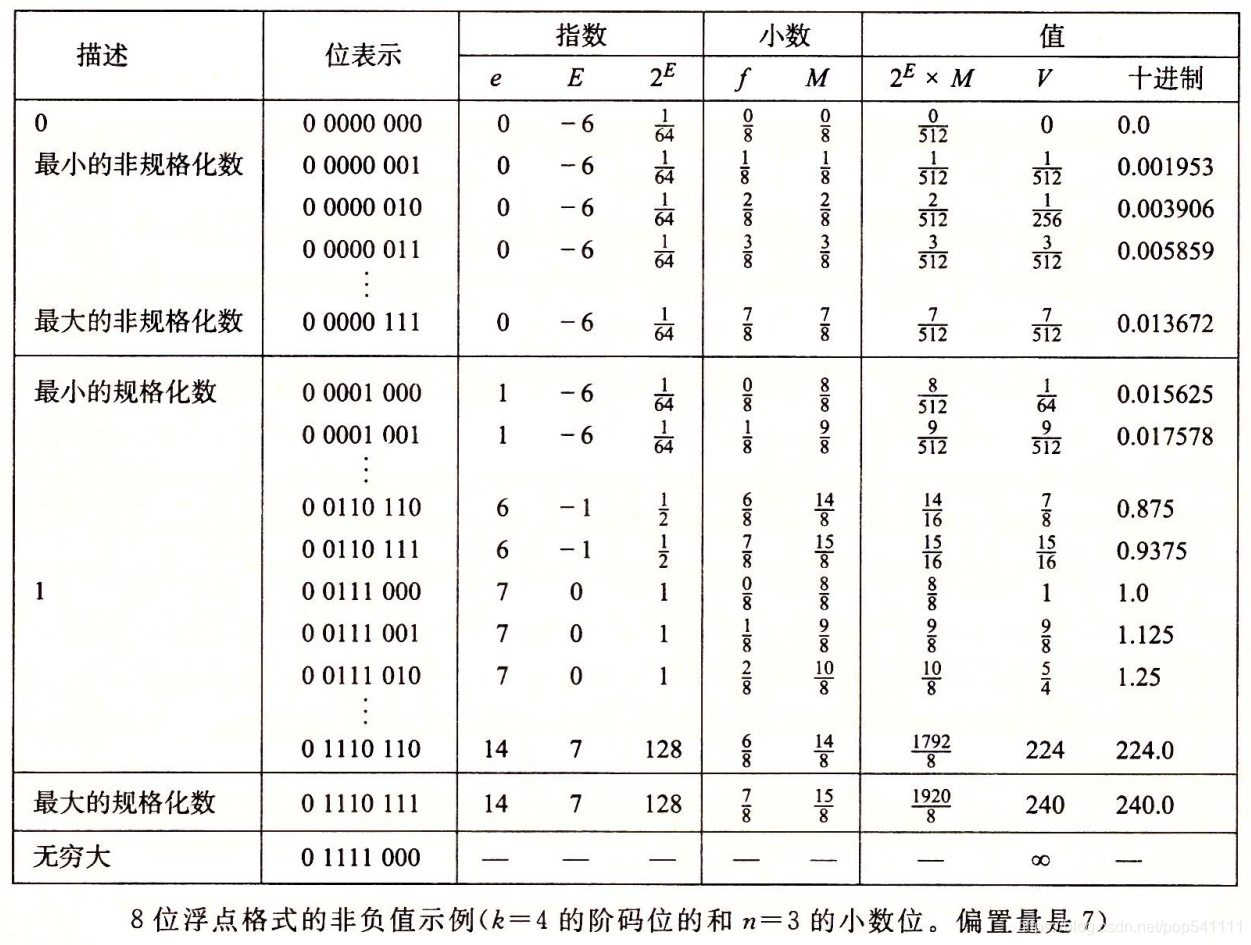
 可以观察到最大非规格化数$\frac{7}{512}$和最小规格化数$\frac{8}{512}$之间的平滑转变。这种平滑性归功于我们对非规格化数的 $E$ 的定义。通过将 $E$ 定义为 $1-Bias$，而不是 $Bias$，我们可以补偿非规格化数的尾数没有隐含的开头的1。

 同时在机器中存储的浮点数据会出现精度缺失和大数吃小数