PyTorch学习——利用梯度下降法实现一元线性回归

一元线性回归

一元线性模型非常简单，假设我们有变量 $x_i$ 和目标 $y_i$，每个 i 对应于一个数据点，希望建立一个模型

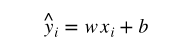
${\hat{y}}_i$ 是我们预测的结果，希望通过 ${\hat{y}}_i$ 来拟合目标 $y_i$，通俗来讲就是找到这个函数拟合 $y_i$ 使得误差最小，即最小化

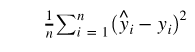
梯度

梯度在数学上就是导数，如果是一个多元函数，那么梯度就是偏导数。比如一个函数f(x, y)，那么 f 的梯度就是
$$(\frac{\partial f}{\partial x},\frac{\partial f}{\partial y})$$

可以称为 grad f(x, y) 或者 $\nabla f(x,y)$。具体某一点 $(x_0,y_0)$ 的梯度就是 $\nabla f(x_0,y_0)$。

梯度有什么意义呢？从几何意义来讲，一个点的梯度值是这个函数变化最快的地方，具体来说，对于函数 f(x, y)，在点 $(x_0,y_0)$ 处，沿着梯度 $\nabla f(x_0,y_0)$ 的方向，函数增加最快，也就是说沿着梯度的方向，我们能够更快地找到函数的极大值点，或者反过来沿着梯度的反方向，我们能够更快地找到函数的最小值点。

梯度下降法

有了对梯度的理解，我们就能了解梯度下降法的原理了。上面我们需要最小化这个误差，也就是需要找到这个误差的最小值点，那么沿着梯度的反方向我们就能够找到这个最小值点。

我们可以来看一个直观的解释。比如我们在一座大山上的某处位置，由于我们不知道怎么下山，于是决定走一步算一步，也就是在每走到一个位置的时候，求解当前位置的梯度，沿着梯度的负方向，也就是当前最陡峭的位置向下走一步，然后继续求解当前位置梯度，向这一步所在位置沿着最陡峭最易下山的位置走一步。这样一步步的走下去，一直走到觉得我们已经到了山脚。当然这样走下去，有可能我们不能走到山脚，而是到了某一个局部的山峰低处。

类比我们的问题，就是沿着梯度的反方向，我们不断改变 w 和 b 的值，最终找到一组最好的 w 和 b 使得误差最小。

在更新的时候，我们需要决定每次更新的幅度，比如在下山的例子中，我们需要每次往下走的那一步的长度，这个长度称为学习率，用 $\eta$ 表示，这个学习率非常重要，不同的学习率都会导致不同的结果，学习率太小会导致下降非常缓慢，学习率太大又会导致跳动非常明显。

最后我们的更新公式就是
$$\begin{gathered} w:=w-\eta \frac{\partial f(w,b)}{\partial w} \\ b:=b-\eta \frac{\partial f(w,b)}{\partial b} \end{gathered}$$

通过不断地迭代更新，最终我们能够找到一组最优的 w 和 b，这就是梯度下降法的原理。

PyTorch实现一元线性回归

待拟合实验数据

import torch
import numpy as np
from torch.autograd import Variable
import matplotlib.pyplot as plt

x_train = np.array([[3.3], [4.4], [5.5], [6.71], [6.93], [4.168],
                    [9.779], [6.182], [7.59], [2.167], [7.042],
                    [10.791], [5.313], [7.997], [3.1]], dtype=np.float32)

y_train = np.array([[1.7], [2.76], [2.09], [3.19], [1.694], [1.573],
                    [3.366], [2.596], [2.53], [1.221], [2.827],
                    [3.465], [1.65], [2.904], [1.3]], dtype=np.float32)


plt.plot(x_train, y_train, 'bo')
plt.show()

显示图像：

模型定义和初始化

# 转换成 Tensor
x_train = torch.from_numpy(x_train)
y_train = torch.from_numpy(y_train)

# 定义参数 w 和 b
w = Variable(torch.randn(1), requires_grad=True)  # 随机初始化
b = Variable(torch.zeros(1), requires_grad=True)  # 使用 0 进行初始化

# 构建线性回归模型
x_train = Variable(x_train)
y_train = Variable(y_train)


def linear_model(x):
    return x * w + b


y_ = linear_model(x_train)

plt.plot(x_train.data.numpy(), y_train.data.numpy(), 'bo', label='real')
plt.plot(x_train.data.numpy(), y_.data.numpy(), 'ro', label='estimated')
plt.show()

这个时候需要计算我们的误差函数，也就是

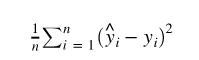
# 计算误差
def get_loss(y_, y):
    return torch.mean((y_ - y_train) ** 2)

loss = get_loss(y_, y_train)
# 打印一下看看 loss 的大小
print(loss)

定义好了误差函数，接下来我们需要计算 w 和 b 的梯度了

# 自动求导
loss.backward()
# 查看 w 和 b 的梯度
print(w.grad)
print(b.grad)

更新一次参数

# 更新一次参数
w.data = w.data - 1e-2 * w.grad.data
b.data = b.data - 1e-2 * b.grad.data
y_ = linear_model(x_train)
plt.plot(x_train.data.numpy(), y_train.data.numpy(), 'bo', label='real')
plt.plot(x_train.data.numpy(), y_.data.numpy(), 'ro', label='estimated')
plt.show()

从上面的例子可以看到，更新之后红色的线跑到了蓝色的线下面，没有特别好的拟合蓝色的真实值，所以我们需要在进行几次更新

循环更新

for e in range(10):  # 进行 10 次更新
    y_ = linear_model(x_train)
    loss = get_loss(y_, y_train)

    w.grad.zero_()  # 记得归零梯度
    b.grad.zero_()  # 记得归零梯度
    loss.backward()

    w.data = w.data - 1e-2 * w.grad.data  # 更新 w
    b.data = b.data - 1e-2 * b.grad.data  # 更新 b
    print('epoch: {}, loss: {}'.format(e, loss.item()))


y_ = linear_model(x_train)
plt.plot(x_train.data.numpy(), y_train.data.numpy(), 'bo', label='real')
plt.plot(x_train.data.numpy(), y_.data.numpy(), 'ro', label='estimated')
plt.show()

tensor(13.2937, grad_fn=<MeanBackward0>)
tensor([-47.0074])
tensor([-6.9313])
epoch: 0, loss: 0.46915704011917114
epoch: 1, loss: 0.23152294754981995
epoch: 2, loss: 0.22683243453502655
epoch: 3, loss: 0.22645452618598938
epoch: 4, loss: 0.22615781426429749
epoch: 5, loss: 0.2258642166852951
epoch: 6, loss: 0.22557203471660614
epoch: 7, loss: 0.22528137266635895
epoch: 8, loss: 0.22499223053455353
epoch: 9, loss: 0.2247045636177063

经过 10 次更新，我们发现红色的预测结果已经比较好的拟合了蓝色的真实值。