【数据结构_12】优先级队列

一、优先级队列的使用

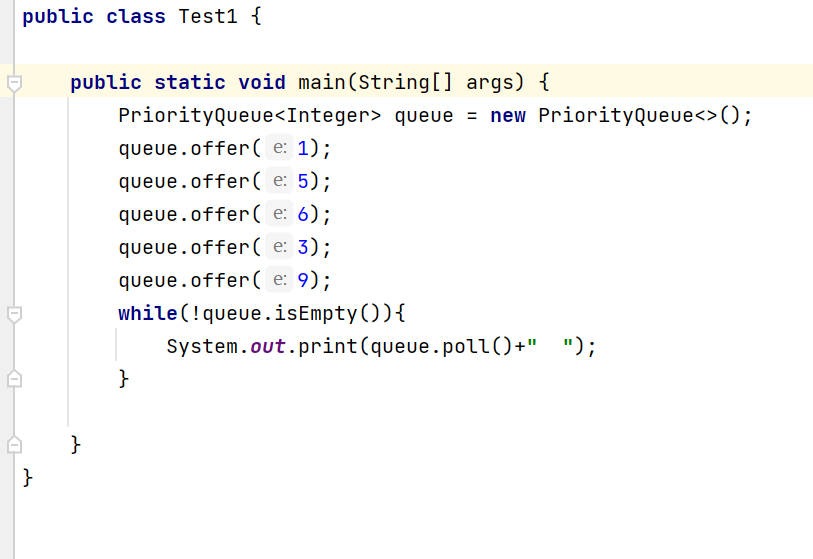
 输出：

通过以上例子我们可以看出，优先级队列是一个“特殊”的队列，正常的队列的顺序是“先进先出”，优先级队列，出队列的顺序和入队列的是不一样的，是把队列中的每个元素，都约定了“优先级”，出队列的时候把优先级最高的元素先出队列。

如果仅仅是把 “ 整数 / 字符串 ”放到优先级队列，元素自身就带有规则。如果优先级队列中的元素是对象，我们就需要掂量以下具体的规则了。

二、优先级队列的原理
优先级队列并不是通过顺序表/链表来表示的，因为如果是通过遍历顺表或者链表来把最小的元素找到并进行删除，这样的思路固然可以，但他的时间复杂度是O（N）。

*通常我们认为O（1）是最小的，P（logN） 当N是非常大的时候，无线趋近于水平线 ，而O（N）比logN大很多

因此，我们是通过“堆”来实现优先级队列的。

1.堆的概念

堆是一个完全二叉树，他是通过数组的方式来存储的完全二叉树

针对完全二叉树，可以不适用“孩子表示法”，而是可以通过更简单的“数组”的方式来表示

把这个树层序遍历，遍历的结果，依次添加到数组中，中间如果遇到空节点，把空节点也添加到数组中。

*为什么前面不用数组的方式来表示二叉树呢？

e.g.

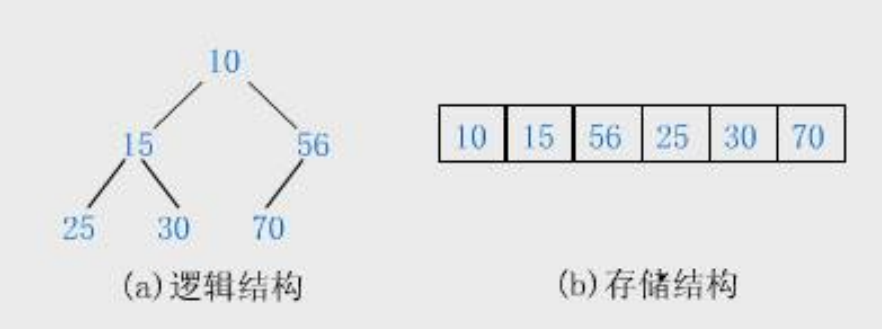
比方说图上这棵树，如果用数组去表示，那么我们就会得到如下这一个数组：

放进去null是为了维护父子之间的下标关系，通过举例发现：普通的二叉树，可能包含大量的null，导致整个数组，里面也包含大量的null，导致整体的内存利用率降低。

而堆是一个完全二叉树，所以不会出现内存利用率低的情况。

通过数组，我们可以更快地得到父节点与子节点的关系：

设父节点的下标为parent，那么左子树的下标就是2*parent+1，右子树的下标就是2*parent+2。

设子节点下标为child，父节点的下标也就是（child-1）/2。（*因为0/2=0，1/2=0）

2.对于堆来说，约定，任何一个节点的值都是小于（或大于）两个子节点的值（这俩子节点谁大谁小没关系）

堆的树根节点（数组的[0]下标的元素，就是整棵树的最小值）

在这颗树中，我们可以通过O（1）复杂度就能找到值最小的元素—>优先级队列

小堆示例：

大堆示例：

接下来我们来考虑如何用代码来实现堆

对于给定的一个任意数组，将他调整成符合堆要求的结构

（1）首先，我们来考虑一个最简单的情况：有一个数组，除了0下标的元素之外，其他的元素都满足小堆的要求。

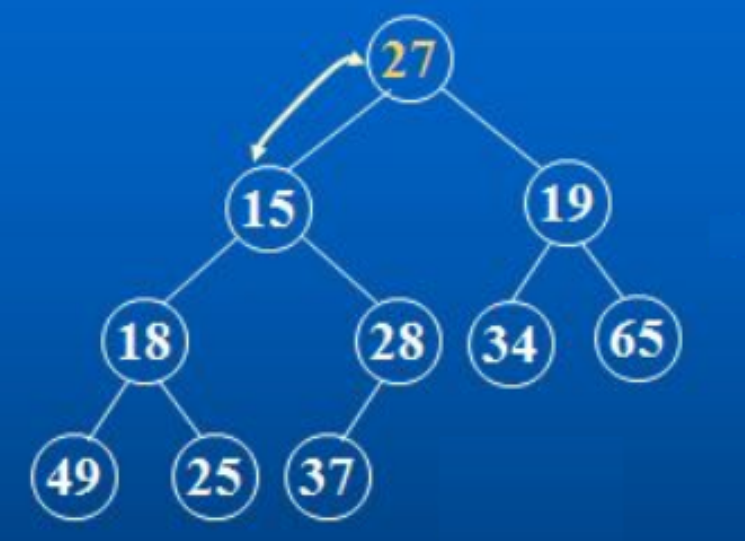
如图所示，针对这种情况，此时我们的方案就是“向下调整”：
1.先确定要比较的子节点是哪一个？

（a）如果只有左子树，那么要比较的就是这个左子树

（b）如果同时又左右子树，先比较左右子树哪个更小，然后取更小的那个

（*此处不考虑只有右子树的情况，因为堆是完全二叉树）

2.拿着刚才这个更小的左右子树的节点，和根节点进行比较和交换

如果发现根节点比子节点大，那就交换这两个节点的值

重复此过程直到该结构符合要求。

*向下调整/下沉式调整：进行向下调整的前提是除了根节点之外，其他的节点，都已经符合堆的要求，随便给个数组，直接向下调整一次，是不足以构建出整个堆的。

对于堆来说，数组是一个完全二叉树，取出整个数组中最后一个“非叶子节点”，从这个节点开始，从后往前地进行向下调整。由于当前是从最后一个非叶子节点开始进行调整的，此时意味着该系欸但的子节点一定是叶子（叶子意味着没有子树），因此叶子自身就可以认为是一个合法的堆。

一个向下调整的过程：

总结：构建堆的基本思路：

1.从最后一个非叶子节点出发，从后往前遍历，针对每个节点，进行向下调整

2.所谓的向下调整，找出子树中的最小值，和根节点比较，如果根节点大，就和刚才的子树节点交换，持续往下进行直到根节点比子树小，或者没有子树的时候

左子树下标：2*parent+1

右子树下标：2*parent+2

package PriorityQueue;

public class Heap {

    //先写一个向下调整的方法
    public static void ShiftDown(int[] array, int index){
        int parent = index;
        int child = parent *2+1;
        while(child <array.length){
            if ((child+1<array.length) && array[child + 1] < array[child] ) {
                child = child +1;
                }
            if(array[parent]<= array[child]){
                break;
            }else{
                int tmp = array[child];
                array[child] = array[parent];
                array[parent] = tmp;
                parent = child;
                child = 2*parent+1;
            }
            }
        }

        public static void createHeap(int[] array){
        int lastLeaf = array.length -1;
        int lastParent = (lastLeaf-1)/2;
        for(int i = lastParent;i>=0;i--){
            ShiftDown(array,i);
        }
        }

    public static void main(String[] args) {
        int[] array ={1,5,6,2,4,3};
        createHeap(array);
        for(int i=0;i<array.length;i++){
            System.out.print(array[i]+"  ");
        }
    }