机器学习之回归

一. 线性回归 (Linear model)

1. 引入

分类中最直白的就是二分类，而且为线性可分。就以房价预测为例，价格的变动与面积，房间个数有关，那么写出其基本形式：$$h_{\theta }(x)={\theta }_0+{\theta }_1{x}_1+{\theta }_2{x}_2{h}_{\theta }(x)=s\sum _{i=0}^n{\theta }_i{x}_i={\theta }^{T}x$$
$x$ 表示特征，$\theta$ 表示权重，${\theta }_0$ 表示偏置

2. 损失函数

任何计算公式都是有误差的，因此我们就要求得最小误差下的 $\theta$，我们把 $x$ 到 $y$ 的映射函数 $f$ 记作 $\theta$ 的函数 $h_{\theta }(x)$，定义 损失函数 (cost function) 为 ：$$J({\theta }_0,{\theta }_1,\cdots ,{\theta }_n)=\frac{1}{2m}\sum _{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)}{)}^2$$
此函数用来描述 $h_{\theta }(x^{(i)})$ 与对应的 $y^{(i)}$ 的接近程度，$\frac{1}{2}$ 只是系数，便于求导，并无影响。目前的问题转换为求满足最小 $J(\theta )$ 的 $\theta$

3. 梯度下降

梯度下降是逐步最小化损失函数的过程，我们对 $\theta$ 设定一个随机初值 ${\theta }_0$，然后带入下式进行迭代:
$$\theta :=\theta -\alpha \frac{d}{d\theta }J(\theta )$$

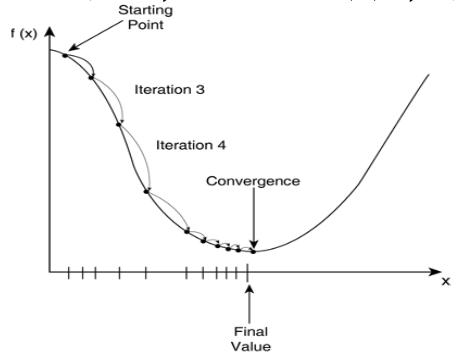
式中 $\alpha$ 为学习率，即每一步向下的跨度，学习率可以影响收敛速度，但选取过大容易得到局部最优解。

4. 最小二乘法

最小二乘法是直接利用矩阵运算得到 $\theta$ ，假设n个特征(变量) $x_n$，用矩阵表示 $X$，结果为 $\vec{y}$，可以得出$$\theta =(X^{T}X{)}^{-1}{X}^T\vec{y}$$
详细推导请查看 最小二乘法求 $\theta$。现实的数据中 $X^{T}X$ 往往不是满秩矩阵，此时可解出多个 $\theta$ 使得均方误差最小化，选择输出解将由学习算法的归纳偏好决定，常见的做法是引入正则化项。

5. 拟合问题

如果我们特征过多，使得 $J(\theta )\approx 0$，会对原数据拟合得非常好，但是预测效果会变差。我们引入正则化 (误差分析)：
$$J({\theta }_0,{\theta }_1,\cdots ,{\theta }_n)=\frac{1}{2m}[\sum _{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)}{)}^2+\lambda \sum _{j=1}^n{\theta }_j^2]$$

注意： $\lambda$ 是需要自己设定得参数，太小容易过拟合，太大基本上不会拟合出决策边界。

二. 逻辑斯特回归

1. logistic回归

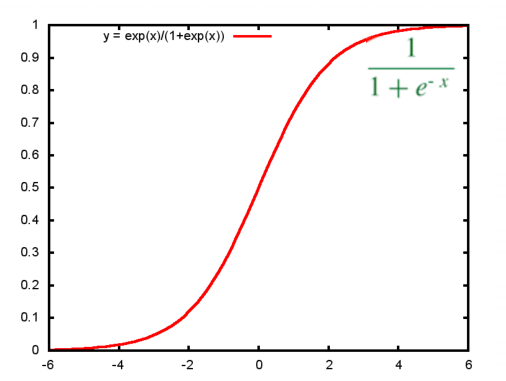
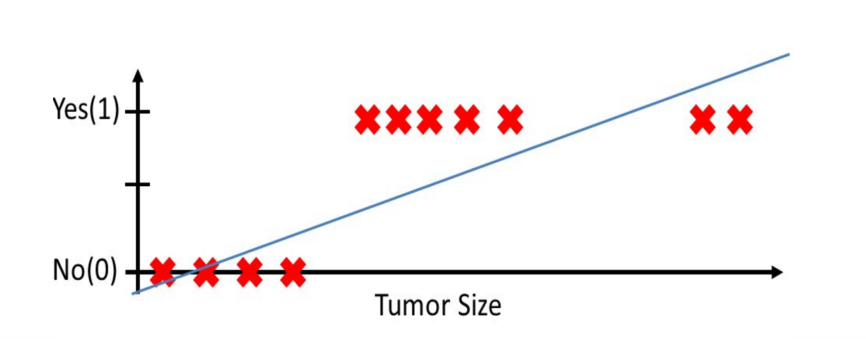
强调： logistic回归是本质仍然是线性回归，但它一种分类算法，因为有些连续值是根据阈值而分开，因此引入一个函数映射——sigmoid函数。

引入这个函数就很容易对下图进行分类

2. 逻辑斯特回归假设

$$h_{\theta }(x)=g({\theta }^{T}x)g(z)=\frac{1}{1+e^{-z}}$$

def sigmoid(z):
    return(1 / (1 + np.exp(-z)))

这个函数在很多集成库中已有，尤其是在框架中直接调用 (正在学习tensorfow)

损失函数：
$$J(\theta )=\frac{1}{m}\sum _{i=1}^m[-y^{(i)}log(h_{\theta }(x^{(i)}))-(1-y^{(i)})log(1-h_{\theta }(x^{(i)}))]$$
向量化的损失函数 (矩阵形式)：
$$J(\theta )=\frac{1}{m}((log(g(X\theta ){)}^{T}y+(log(1-g(X\theta ){)}^T(1-y))$$

def costFunction(theta, X, y):
    m = y.size
    h = sigmoid(X.dot(theta))
    
    J = -1*(1/m)*(np.log(h).T.dot(y)+np.log(1-h).T.dot(1-y))
               
    if np.isnan(J[0]):
        return(np.inf)
    return(J[0])

梯度

$$\frac{\partial J(\theta )}{\partial {\theta }_j}=\frac{1}{m}\sum _{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)})x_j^{(i)}$$
向量化的梯度
$$\frac{\partial J(\theta )}{\partial {\theta }_j}=\frac{1}{m}{X}^T(g(X\theta )-y)$$

def gradient(theta, X, y):
    m = y.size
    h = sigmoid(X.dot(theta.reshape(-1,1)))
    grad =(1/m)*X.T.dot(h-y)

    return(grad.flatten())

3. 岭回归

带正则化项的损失函数
$$J(\theta )=\frac{1}{m}\sum _{i=1}^m[-y^{(i)}log(h_{\theta }(x^{(i)}))-(1-y^{(i)})log(1-h_{\theta }(x^{(i)}))]+\frac{\lambda }{2m}\sum _{j=1}^n{\theta }_j^2$$
向量化的损失函数
$$J(\theta )=\frac{1}{m}((log(g(X\theta ){)}^{T}y+(log(1-g(X\theta ){)}^T(1-y))+\frac{\lambda }{2m}\sum _{j=1}^n{\theta }_j^2$$

梯度

$$\frac{\partial J(\theta )}{\partial {\theta }_j}=\frac{1}{m}\sum _{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)})x_j^{(i)}+\frac{\lambda }{m}{\theta }_j$$

向量化
$$\frac{\partial J(\theta )}{\partial {\theta }_j}=\frac{1}{m}{X}^T(g(X\theta )-y)+\frac{\lambda }{m}{\theta }_j$$

附上一个完整的逻辑回归代码

import numpy as np
import random

def genData(numPoints,bias,variance):
    #产生一个numpoints行，2列的0矩阵
    x = np.zeros(shape=(numPoints,2))
    #一列0矩阵
    y = np.zeros(shape=(numPoints))
    for i in range(0,numPoints):
        x[i][0]=1
        x[i][1]=i
        y[i]=(i+bias)+random.uniform(0,1)+variance
    return x,y

def gradientDescent(x,y,theta,alpha,m,numIterations):
    xTran = np.transpose(x)
    for i in range(numIterations):
        hypothesis = np.dot(x,theta)
        loss = hypothesis-y
        cost = np.sum(loss**2)/(2*m)
        gradient=np.dot(xTran,loss)/m
        theta = theta-alpha*gradient
        print ("Iteration %d | cost :%f" %(i,cost))
    return theta
    
x,y = genData(100, 25, 10)
print ("x:")
print (x)
print ("y:")
print (y)

m,n = np.shape(x)
n_y = np.shape(y)

print("m:"+str(m)+" n:"+str(n)+" n_y:"+str(n_y))

numIterations = 100000
alpha = 0.0005
theta = np.ones(n)
theta= gradientDescent(x, y, theta, alpha, m, numIterations)
print(theta)

这是一个sklearn的应用，数据自己带入即可(二分类问题)

from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import classification_report
import pandas as pd
import numpy as np

colomns = ['','','','','','','','','']
data = pd.read_csv('',names=colomns)
print(data)

# 对缺失值进行处理
data = data.replace(to_replace='?', value=np.nan)
data = data.dropna()

# 分割数据
x_train, y_train, x_test, y_test = train_test_split(data[colomns[1:10]], data[colomns[10]],test_size=0.25)

std = StandardScaler()
x_train = std.fit_transform(x_train)
x_test = std.transform(x_test)

# 逻辑回归预测
lg = LogisticRegression(C=1.0)
lg.fit(x_train, y_train)
y_predict = lg.predict(x_test)

print(lg.coef_)
print("accuracy: ", lg.score(x_test, y_test))
print("recall: ", classification_report(y_test, y_predict, labels=[2,4], target_names=['','']))

三. 参考链接

[1] 机器学习有监督学习之–回归
[2] 线性回归，逻辑回归 深入浅出
[3] 《机器学习》 周志华