本篇为您解决以下几个问题
- 怎么判断一个链表有环?
- 怎么获得入环处?
- 怎么知道环大小?
进阶后方会附上证明
答案
一、怎么判断一个链表有环?
快慢指针如果相遇就有环
二、怎么获得入环处?
快慢指针相遇后,快指针回到链表头,而后和慢指针一样一次走一步,再次相遇时就是入环处
三、怎么知道环大小?
必须要入环处再走一圈才能得到环大小,并不是快慢指针第一次相遇时候的步数
进阶
演示
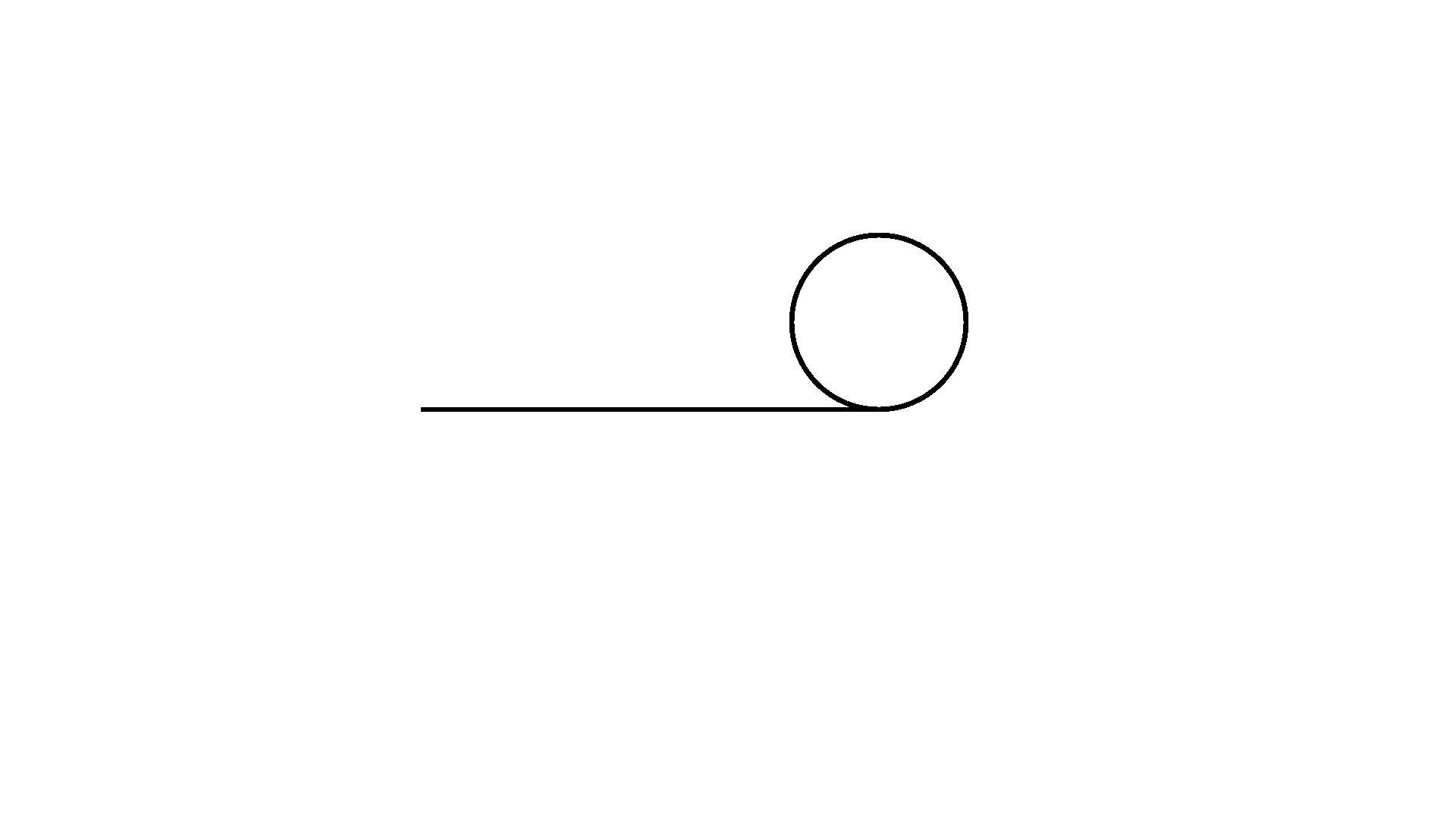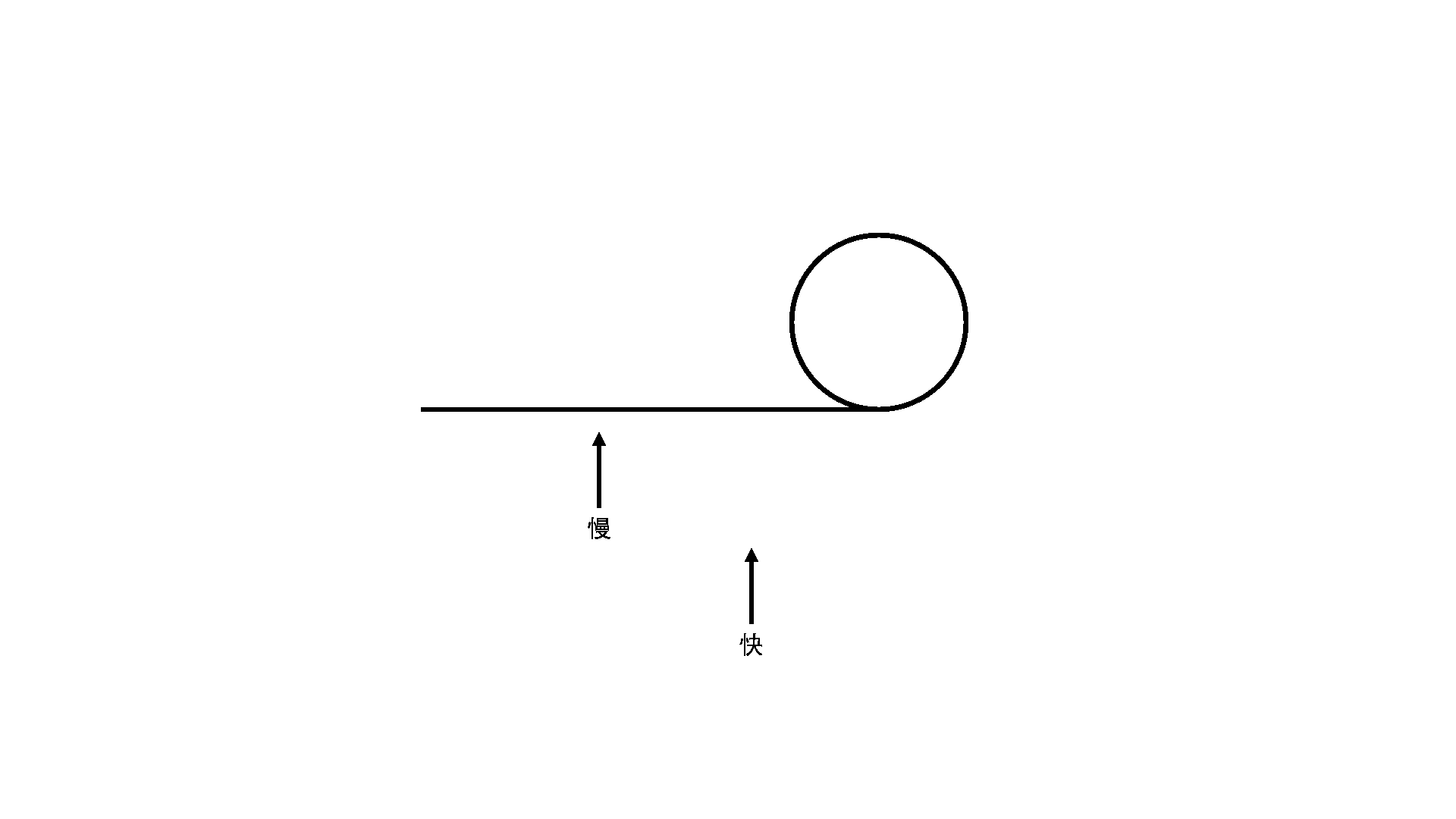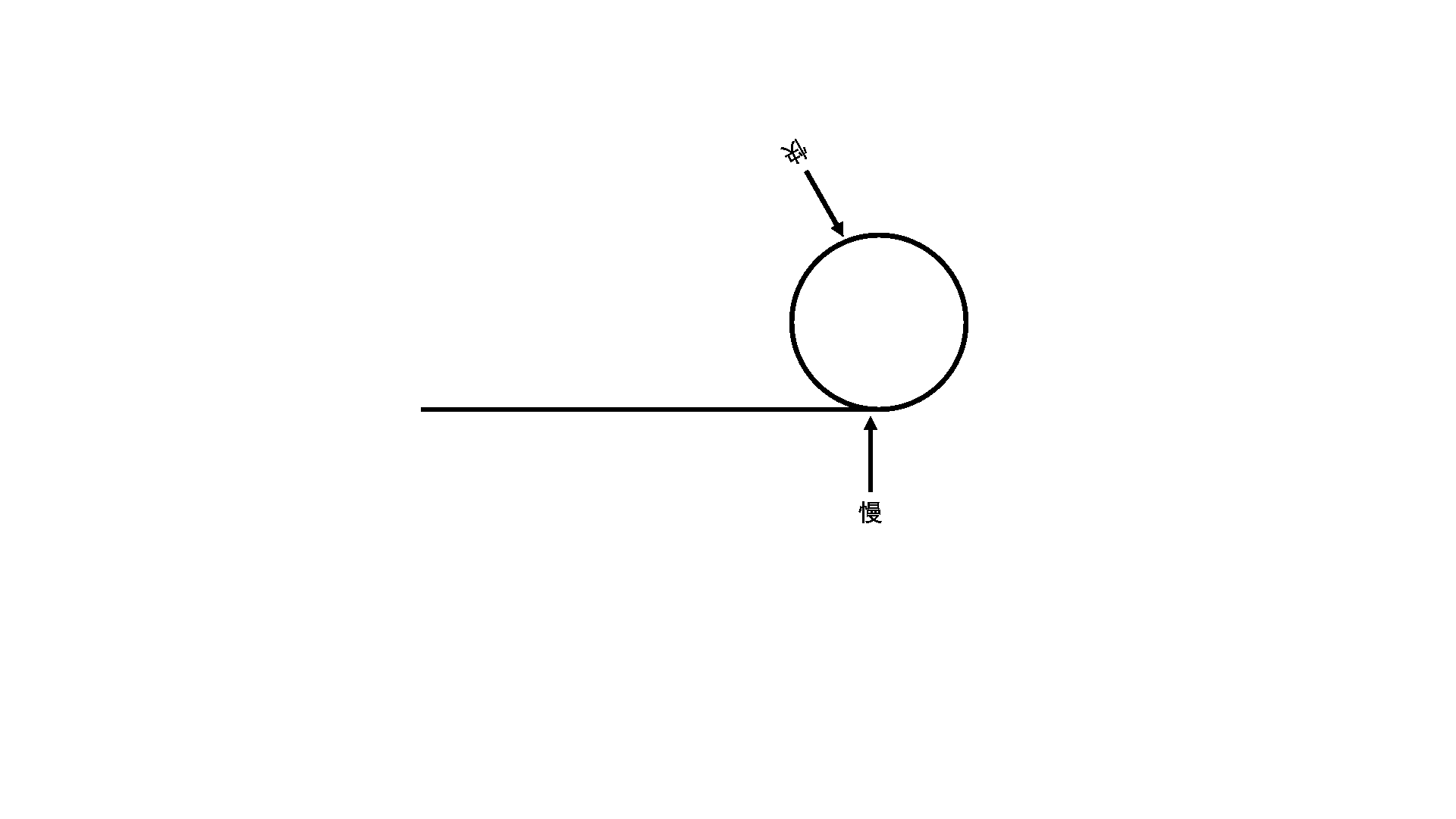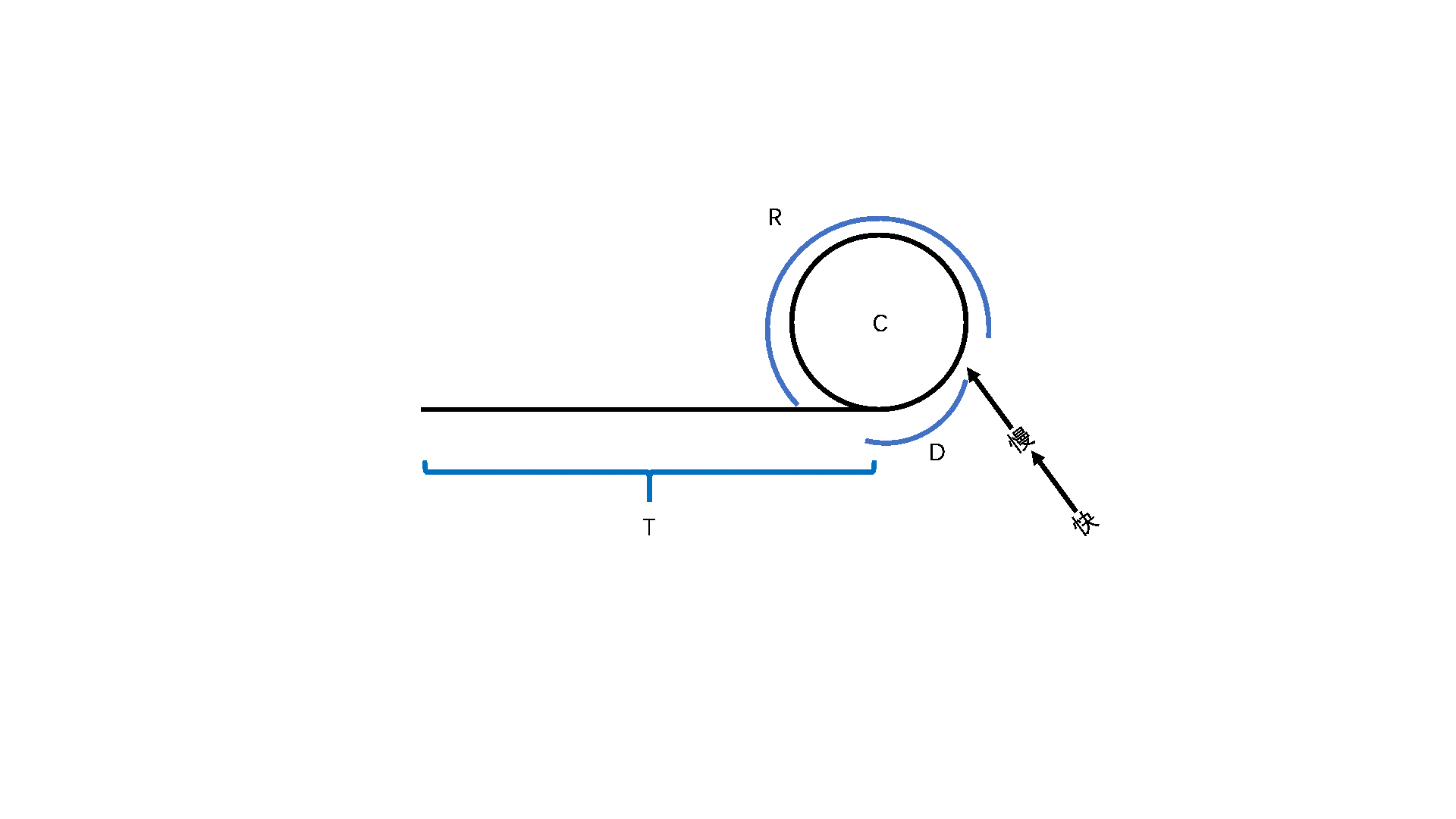
快慢指针相遇时链表结构如下图所示
名词解释
T : T a i l , 表 头 到 入 环 处 的 距 离 D : D i s t a n c e , 入 环 处 到 快 慢 指 针 相 遇 处 的 距 离 C : C i r c l e , 环 的 大 小 R : R e m i n d , 快 慢 指 针 相 遇 处 到 入 环 处 的 距 离 ( 顺 时 针 走 ) i : 快 慢 指 针 相 遇 时 快 指 针 环 内 走 过 的 圈 数 j : 快 慢 指 针 相 遇 时 慢 指 针 环 内 走 过 的 圈 数 k : 快 指 针 回 到 表 头 后 快 慢 指 针 一 起 走 , 慢 指 针 走 的 圈 数 S : 快 慢 指 针 相 遇 时 慢 指 针 环 内 走 过 的 步 数 n : i − j 快 慢 指 针 相 遇 时 快 慢 指 针 走 过 的 圈 数 的 差 \begin{aligned}&T:Tail,表头到入环处的距离\\&D:Distance,入环处到快慢指针相遇处的距离\\&C:Circle,环的大小\\&R:Remind,快慢指针相遇处到入环处的距离(顺时针走)\\&i:快慢指针相遇时快指针环内走过的圈数\\&j:快慢指针相遇时慢指针环内走过的圈数\\&k:快指针回到表头后快慢指针一起走,慢指针走的圈数\\&S:快慢指针相遇时慢指针环内走过的步数\\&n:i-j快慢指针相遇时快慢指针走过的圈数的差\end{aligned} T:Tail,表头到入环处的距离D:Distance,入环处到快慢指针相遇处的距离C:Circle,环的大小R:Remind,快慢指针相遇处到入环处的距离(顺时针走)i:快慢指针相遇时快指针环内走过的圈数j:快慢指针相遇时慢指针环内走过的圈数k:快指针回到表头后快慢指针一起走,慢指针走的圈数S:快慢指针相遇时慢指针环内走过的步数n:i−j快慢指针相遇时快慢指针走过的圈数的差
假设
- 不知道快慢指针各走了多少圈
一、证明为什么环就一定会相遇?
反证法,假设有个操场,你在刘翔后面跑,大家都不停,请问你会不会被超圈?
二、证明入环处是这样得到的正确性?
看相遇时候的步数
首先只看慢指针,慢指针的步数为 S = T + D + j C S=T+D+jC S=T+D+jC
然后看快指针,快指针的步数为 2 S = T + D + i C 2S=T+D+iC 2S=T+D+iC
两者相减为 S = ( i − j ) C = n C S=(i-j)C=nC S=(i−j)C=nC
也就是说,相遇的时候,快指针正好超车 n n n圈
这个时候快指针回到起点处,慢指针继续走,看图
T T T步以后快指针从表头走了 T T T到达入环处,慢指针从表头走了 S + T S+T S+T步,慢指针比快指针多走了 S = n C S=nC S=nC,刚好 n n n圈,也就是说在入环处此时快慢指针相遇
三、证明环大小正确性?
入环处走了一圈回到入环处,当然是环大小了
四、环大小为什么不是 S S S?
这个问题困扰我多年,先上结论:
因为 T T T不一定等于 R R R, T = R + k C T=R+kC T=R+kC, k k k不一定 = 0 =0 =0
看到很多博客说,环大小就是第一次相遇时 S S S的大小,大错特错!
因为他们假设是第二次相遇时候,慢指针只走了 R R R的距离,就到达了入环处,实际情况是,慢指针可能走了 R + k C R+kC R+kC的距离才到达入环处!也就是说,慢指针走到了入环处的时候,又走了 k k k圈才等到快指针!自己画图可以把 T T T设置大一点, C C C设置小一点就能看出来了


























 3235
3235











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








