欧式二元期权的定价公式及实现

本文将从文献中查阅欧式二元期权的定价公式，用代码实现该公式。

公式来自于文献[1]。文中用到的部分函数，请参考上一篇文章。

于是，二元看涨（看跌我就不写了）

def calc_price(s, k, t, v, r, d, payout):
    """
    二元看涨期权定价公式
    :param s: 当前标的价格
    :param k: 行权价
    :param t: 距离到期时间（以“年”为单位）
    :param v: 波动率
    :param r: 无风险利率
    :param d: 分红率（连续复利）
    :param payout: 行权收益
    :return: 
    """
    price = np.exp(-r * t) * norm.cdf(
        blsd(s / k, r - d - 0.5 * v * v, v, t)) * payout

    return price

 

另外，关于二元看涨期权的Greeks。

在临近到期、标的价格在行权价附近时，Delta、Gamma会异常巨大！

在实务对冲中，不可能会以这样庞大的delta去持有对冲头寸的。

1. 对冲工具流动性不足，真要买这么多，估计要被判操纵市场了。

2. Gamma（二阶导）会巨大，造成Delta巨幅震荡，无法实时对冲。

3. 对冲手续费高昂。

TODO 待验证

1. 设置一个Delta阈值。在阈值以上，就不对冲了，在阈值一下，还可以对冲。效果怎样，未知。

2. 期初用垂直价差（vertical spread）静态复制？

3. 挪行权价？那对冲下来会是怎样的效果？

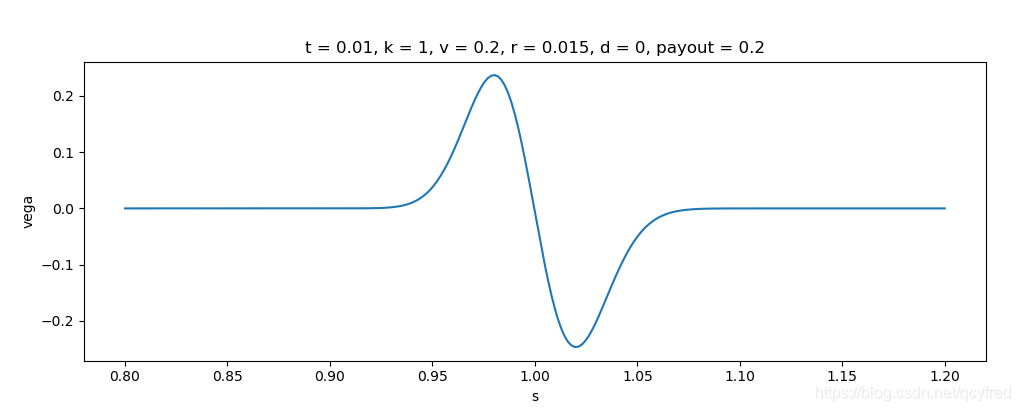
二元看涨期权的Vega与标的价格的关系图。

结论1

s<k，Vega>0，波动大，才可能最终超过行权价，才可能得到收益，否则就是0。

s>k，Vega<0，此时此刻，s最好不动，保住胜利的果实，我就能有收益。波动越大，越不利。

结论2

Vega随着t的流逝，双峰越来越趋近于行权价。 在以k作为临界点看，Vega虽然都是同号，但也有个峰。Vega对s的导数也不是线性的。TODO 高阶风险，未知。

 

 

Ref.

[1] 约翰·赫尔. 期权、期货及其他衍生产品[M]. 机械工业出版社, 2016.