LeetCode - 11 盛最多水的容器

题目来源

11. 盛最多水的容器 - 力扣（LeetCode）

题目描述

给定一个长度为 n 的整数数组 height 。有 n 条垂线，第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。

找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。

返回容器可以储存的最大水量。

说明：你不能倾斜容器。

示例1

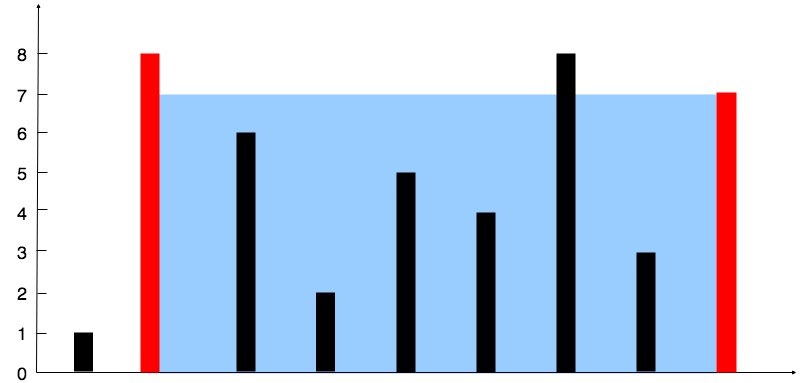
输入：[1,8,6,2,5,4,8,3,7]
输出：49 
解释：图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49。

示例 2

输入：height = [1,1]
输出：1

提示

• n == height.length
• 2 <= n <= 105
• 0 <= height[i] <= 10^4

题目解析

本题可以利用双指针+贪心解题。

容器内水的容量大小 V，取决于容器两端中的较短柱子h_min，因此为了使得容器内水尽可能的多，我们应该找到距离 h_min 柱子最远的，且高度>= h_min 的另一个柱子。 

我们可以定义两个指针 L, R，分别指向 height 数组的首尾元素。

• 若 height[L] < height[R]，则说明 height[L] 是矮柱，而 height[R] 是距离 height[L] 最远的比它高的柱子，因此此时我们找到了 height[L] 作为容器矮柱的最优解。之后 L ++ 。
• 若 height[L] > height[R]，则说明 height[R] 是矮柱，而 height[L] 是距离 height[R] 最远的比它高的柱子，因此此时我们找到了 height[R] 作为容器矮柱的最优解。之后 R -- 。
• 若 height[L] == height[R]，则任意一个柱子作为矮柱都可以。

循环处理上面逻辑，直到 L >= R 时停止。

可能大家会有疑问，随着 L，R的内向移动，可能有一些矮柱无法找到最远的稍高柱子，比如下面例子：

可以发现，此时 L 作为矮柱，对应的最优解高柱应该是 R1，而不是 R。

那么为什么选择 L，R 组合，不会影响结果正确性呢？

因为我们通过双指针运动逻辑可知，R1在之前肯定已经被选作为矮柱过了，且其对应的高柱 L1 肯定是 < L 的。

也就是说 h[R1] * (R1 - L1 + 1) 的结果是肯定大于 h[L] * (R1 - L + 1) 的，因此这里 L 虽然没有匹配到最优高柱 R1，但是 R1 作为矮柱时的容器肯定比当前 R1 作为高柱时的容器盛水更多。

因此，我们可以忽略 R1 作为高柱的情况。

C源码实现

int maxArea(int* height, int heightSize) {
    int l = 0;
    int r = heightSize - 1;

    int ans = 0;

    while (l < r) {
        int h = height[l] <= height[r] ? height[l++] : height[r--];
        ans = (int)fmax(ans, h * (r - l + 1));
    }

    return ans;
}

C++源码实现

class Solution {
public:
    int maxArea(vector<int>& height) {
        int l = 0;
        int r = height.size() - 1;

        int ans = 0;

        while (l < r) {
            int h = height[l] <= height[r] ? height[l++] : height[r--];
            ans = max(ans, h * (r - l + 1));
        }

        return ans;
    }
};

Java源码实现

class Solution {
    public int maxArea(int[] height) {
        int l = 0;
        int r = height.length - 1;

        int ans = 0;

        while (l < r) {
            int h = height[l] < height[r] ? height[l++] : height[r--];
            ans = Math.max(ans, h * (r - l + 1));
        }

        return ans;
    }
}

Python源码实现

class Solution(object):
    def maxArea(self, height):
        """
        :type height: List[int]
        :rtype: int
        """
        l = 0
        r = len(height) - 1

        ans = 0

        while l < r:
            if height[l] <= height[r]:
                h = height[l]
                l += 1
            else:
                h = height[r]
                r -= 1
            
            ans = max(ans, h * (r - l + 1))
        
        return ans

JavaScript源码实现

/**
 * @param {number[]} height
 * @return {number}
 */
var maxArea = function (height) {
    let l = 0;
    let r = height.length - 1;

    let ans = 0;

    while (l < r) {
        const h = height[l] <= height[r] ? height[l++] : height[r--];
        ans = Math.max(ans, h * (r - l + 1));
    }

    return ans;
};