二叉树
二叉树是一颗每个结点都不能多于两个儿子的树。
结点实现
具有N个结点的每一颗二叉树都需要N+1个NULL链。

//二叉树结点类
struct BinaryNode
{
Comprarable element; //The data in the node;
BinaryNode *left; //left child
BinaryNode *right; //right child
};表达式树
表达式树的树叶是操作数,如常数或变量名字,而其他的结点为操作符。
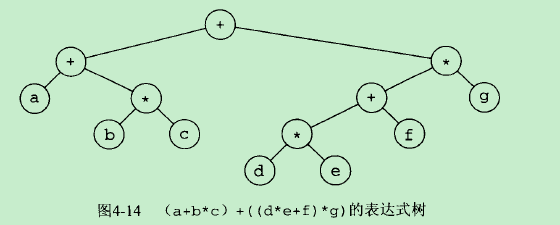
表达式:aXb+(c-d/e)Xf
前缀式:+XabX-c/def
中缀式:aXb+c-d/eXf(无意义)
后缀式:abXcde/-fX+
构造一颗表达式树

表达式:(a+b)*(c*(d+e))
后缀式:ab+cde+**
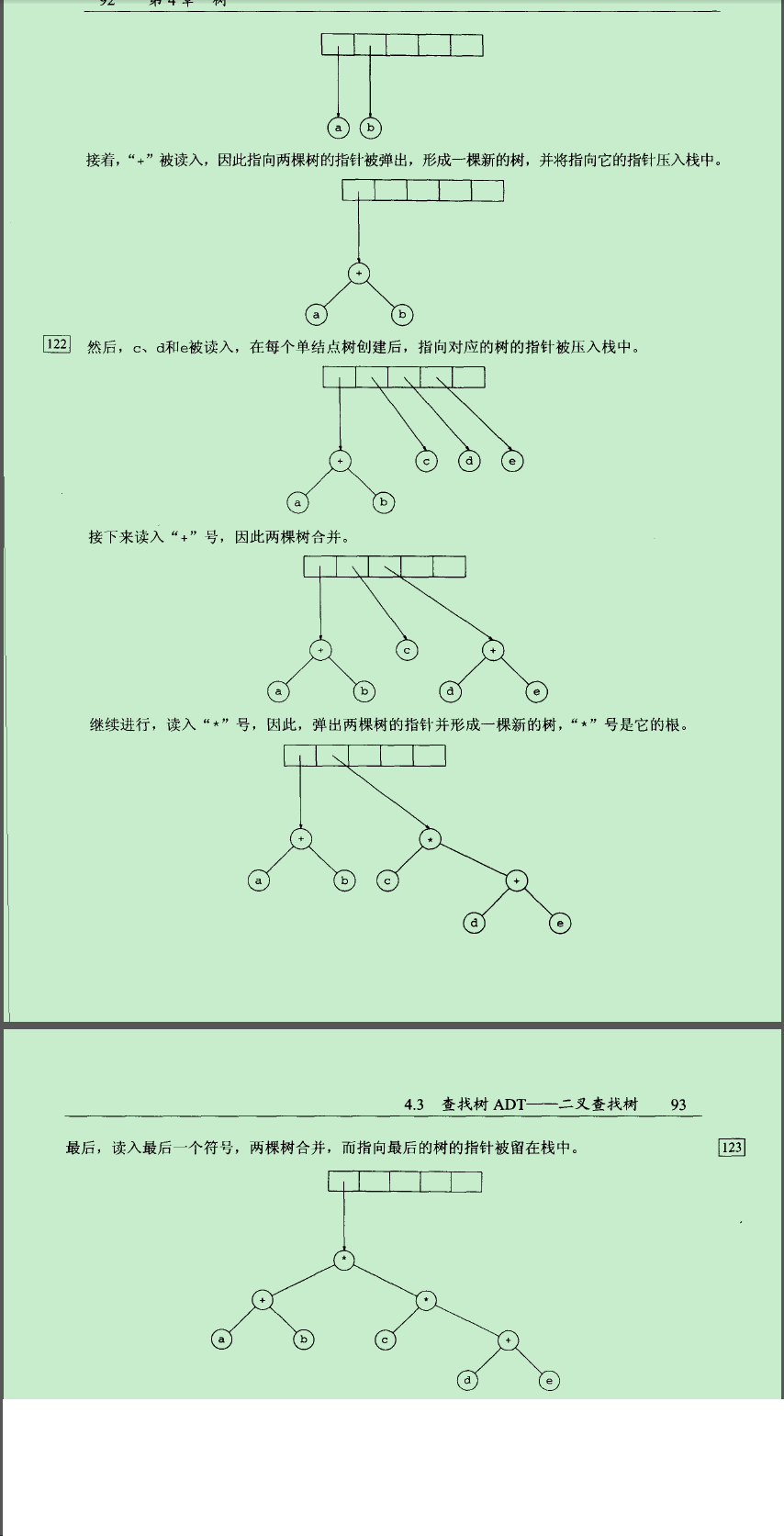
二叉查找树
定义:对于树中的每个结点X,它的左子树中所有项的值小于X中的项,而它的右子树中所有项的值大于X中的项
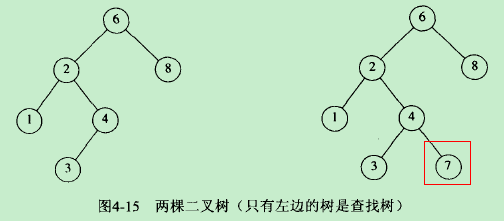

由于树的递归定义,通常是递归的编写这些操作的例程,因为二叉查找树的平均深度是O(logN),所以我们一般不必担心栈空间被用尽。
二叉查找树类的框架:
template<typename Comparable>
class BinarySearchTree
{
public:
BinarySearchTree();
BinarySearchTree(const BinarySearchTree &rhs);
~BinarySearchTree();
const Comparable & findMin() const;
const Comparable & findMax() const;
bool contains(const Comparable &x) const;
bool isEmpty() const;
bool printTree() const;
void makeEmpty();
void insert(const Comparable &x);
void remove(const Comparable &x);
const BinarySearchTree &operator=(const BinarySearchTree &rhs);
private:
//二叉树结点类
struct BinaryNode
{
Comprarable element; //The data in the node;
BinaryNode *left; //left child
BinaryNode *right; //right child
BinaryNode(const Comparable & theElement, BinaryNode *lt, BinaryNode *rt) :
element(theElement), left(lt), right(rt){}
};
BinaryNode *root;
void insert(const Comparable &x, BinaryNode * & r) const;
void remove(const Comparable &x, BinaryNode * & r) const;
BinaryNode * findMin(BinaryNode *t) const;
BinaryNode * findMax(BinaryNode *t) const;
bool contatins(const Comparable &x, BinaryNode *t) const;
void makeEmpty(BinaryNode * & t);
void printTree(BinaryNode * & t) const;
BinaryNode * clone(BinaryNode *t) const;
};数据成员是指向树根结点的指针,该指针对空树为NULL。几个private成员函数使用引指调用来传递指针变量的技术,这允许public成员函数将指向树根的指针传递给private递归成员函数,然后递归函数就可以改变根的值,于是root就可以指向其他的结点。
contains成员函数
如果在树T中有项为X的结点,那么contains操作就返回true,否则,返回false。关键:考虑问题要全面!
//contains
template<typename Comparable>
bool BinarySearchTree<Comparable>::contains(const Comparable &x, BinaryNode *t) const
{
if (t == NULL)
return false;
else if (x < t->element)
return contains(x, t->left);
else if (x > t->elemnet)
return contains(x, t->right);
else
return true;
}
template<typename Comparable>
bool BinarySearchTree<Comparable>::contains(const Comparable &x) const
{
return contains(x, root) const;
}
使用函数对象而不是使用Comparable项所需做的微小修改
template <typename Object, typename Comparator=less<Object> >
class BinarySearchTree
{
public:
// Same methods, with Object replacing Comparable
private:
BinaryNode *root;
Comparator isLessThan;
// Same methods, with Object replacing Comparable
/**
* Internal method to test if an item is in a subtree.
* x is item to search for.
* t is the node that roots the subtree.
*/
bool contains( const Object & x, BinaryNode *t ) const
{
if( t == NULL )
return false;
else if( isLessThan( x, t->element ) )
return contains( x, t->left );
else if( isLessThan( t->element, x ) )
return contains( x, t->right );
else
return true; // Match
}
};
findMax & findMin

//findMin
template<typename Comparable>
typename BinarySearchTree<Comparable>::BinaryNode * BinarySearchTree<Comparable>::findMin(BinaryNode *t) const
{
if (t == NULL)
return NULL;
if (t->left == NULL)
return t;
return findMin(t->left);
}
template<typename Comparable>
const Comparable & BinarySearchTree<Comparable>::findMin() const
{
auto temp = findMin(root);
if (temp == NULL)
{
cout << "The Tree is Empty" << end;
return Comparable();
}
else
return temp->element;
}
//findMax
template<typename Comparable>
<pre code_snippet_id="1687240" snippet_file_name="blog_20160517_5_7322944" name="code" class="cpp">typename BinarySearchTree<Comparable>::BinaryNode * <span style="font-family: Arial, Helvetica, sans-serif;">BinarySearchTree<Comparable>::findMax(BinaryNode *t) const</span>
insert
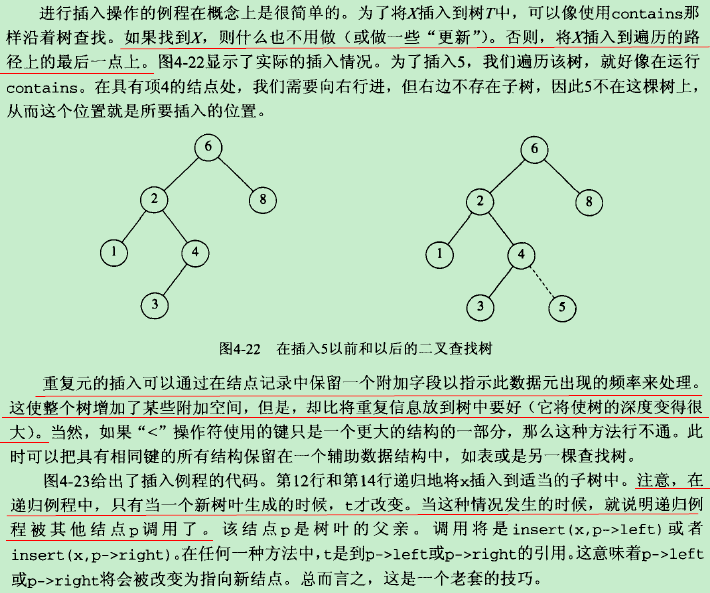
//insert
//公开接口函数
template<typename Comparable>
void BinarySearchTree<Comparable>::insert(const Comparable &x)
{
insert(x, root);
}
//私有函数接口
template<typename Comparable>
void BinarySearchTree<Comparable>::insert(const Comparable &x, BinaryNode * & t) const
{
if (t == NULL)
t = new BinarySearchTree(x, NULL, NULL);
else if (x < t->element)
insert(x, t->left);
else if (x > t->element)
insert(x, t->right);
else
;//Duplicate; do nothing;
}
remove
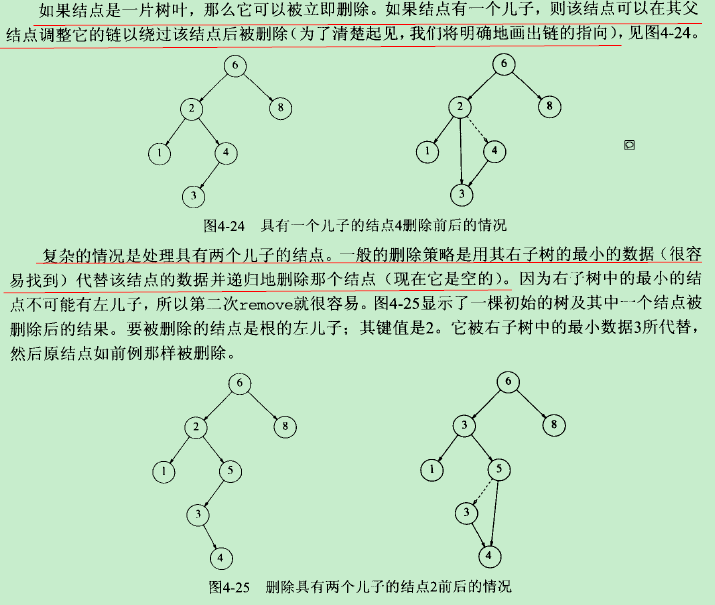
//remove
//公开接口
template<typename Comparable>
void BinarySearchTree<Comparable>::remove(const Comparable &x)
{
remove(x, root);
}
//私有函数
template<typename Comparable>
void BinarySearchTree<Comparable>::remove(const Comparable &x, BinaryNode * &t) const
{
if (t == NULL)
return;
else if (x < t->elemet)
remove(x, t->left);
else if (x > t->element)
remove(x, t->right);
else if (t->left != NULL && t->right != NULL) //two childen
{
t->element = findMin(t->right)->element;
remove(t->element, t->right);//转化为消除单结点
}
else//single child
{
BinaryNode *oldNode = t;
t = (t->left != NULL) ? t->left : t->right;
delete oldNode;
}
}析构函数

//析构函数
template<typename Comparable>
BinarySearchTree<Comparable>::~BinarySearchTree()
{
makeEmpty();
}
template<typename Comparable>
void BinarySearchTree<Comparable>::makeEmpty()
{
makeEmpty(root);
}
template<typename Comparable>
void BinarySearchTree<Comparable>::makeEmpty(BinaryNode * & t)
{
if (t != NULL)
{
makeEmpty(t->left);
makeEmpty(t->right);
delete t;
}
t = NULL;
}深度拷贝
template<typename Comparable>
const BinarySearchTree & BinarySearchTree<Comparable>::operator=(const BinarySearchTree & rhs)
{
if (this != &rhs)
{
makeEmpty();
root = clone(rhs.root);
}
return *this;
}
template<typename Comparable>
BinaryNode * BinarySearchTree<Comparable>::clone(BinarySearchTree *t) const
{
if (t == NULL)
return NULL;
return new BinaryNode(t->element, clone(t->left), clone(t->right));
}源代码:
#ifndef BINARY_SEARCH_TREE_H
#define BINARY_SEARCH_TREE_H
#include<algorithm>
using namespace std;
class UnderflowException { };
template<typename Comparable>
class BinarySearchTree
{
public:
BinarySearchTree() :root(nullptr){};
BinarySearchTree(const BinarySearchTree & rhs) :root(nullptr){ root = clone(rhs.root); };
BinarySearchTree(BinarySearchTree && rhs) :root(rhs.root){ rhs.root = nullptr; }
~BinarySearchTree();
const Comparable & findMin() const;
const Comparable & findMax() const;
bool contains(const Comparable &x) const;
bool isEmpty() const;
void printTree(ostream & out = cout) const;
void makeEmpty();
void insert(const Comparable &x);
void remove(const Comparable &x);
const BinarySearchTree &operator=(const BinarySearchTree & rhs);
const BinarySearchTree &operator=(BinarySearchTree && rhs)
{
std::swap(root, rhs.root);
return *this;
}
private:
//二叉树结点类
struct BinaryNode
{
Comparable element; //The data in the node;
BinaryNode *left; //left child
BinaryNode *right; //right child
BinaryNode(const Comparable & theElement, BinaryNode *lt, BinaryNode *rt) :
element(theElement), left(lt), right(rt){}
};
BinaryNode *root;
void insert(const Comparable &x, BinaryNode * & r) const;
void remove(const Comparable &x, BinaryNode * & r) const;
BinaryNode * findMin(BinaryNode *t) const;
BinaryNode * findMax(BinaryNode *t) const;
bool contains(const Comparable &x, BinaryNode *t) const;
void makeEmpty(BinaryNode * & t);
void printTree(BinaryNode * t, ostream &out = cout) const;
BinaryNode * clone(BinaryNode *t) const;
};
/**
*contains函数,判断该树是否含有某一点
*
*/
//私有函数
template<typename Comparable>
bool BinarySearchTree<Comparable>::contains(const Comparable &x, BinaryNode *t) const
{
if (t == NULL)
return false;
else if (x < t->element)
return contains(x, t->left);
else if (x > t->element)
return contains(x, t->right);
else
return true;
}
//公开接口
template<typename Comparable>
bool BinarySearchTree<Comparable>::contains(const Comparable &x) const
{
return contains(x, root);
}
//findMin
template<typename Comparable>
typename BinarySearchTree<Comparable>::BinaryNode * BinarySearchTree<Comparable>::findMin(BinaryNode *t) const
{
if (t->left == NULL)
return t;
return findMin(t->left);
}
template<typename Comparable>
const Comparable & BinarySearchTree<Comparable>::findMin() const
{
//如果是空,抛出异常
if (isEmpty())
throw UnderflowException{};
return findMin(root)->element;
}
//findMax
template<typename Comparable>
typename BinarySearchTree<Comparable>::BinaryNode * BinarySearchTree<Comparable>::findMax(BinaryNode *t) const
{
if (t->right == NULL)
return t;
return findMax(t->right);
}
template<typename Comparable>
const Comparable & BinarySearchTree<Comparable>::findMax() const
{
//如果是空,抛出异常
if (isEmpty())
throw UnderflowException{};
return findMax(root)->element;
}
//insert
//公开接口函数
template<typename Comparable>
void BinarySearchTree<Comparable>::insert(const Comparable &x)
{
insert(x, root);
}
//私有函数接口
template<typename Comparable>
void BinarySearchTree<Comparable>::insert(const Comparable &x, BinaryNode * & t) const
{
if (t == NULL)
t = new BinaryNode(x, NULL, NULL);
else if (x < t->element)
insert(x, t->left);
else if (x > t->element)
insert(x, t->right);
else
;//Duplicate; do nothing;
}
//remove
//公开接口
template<typename Comparable>
void BinarySearchTree<Comparable>::remove(const Comparable &x)
{
remove(x, root);
}
//私有函数
template<typename Comparable>
void BinarySearchTree<Comparable>::remove(const Comparable &x, BinaryNode * &t) const
{
if (t == NULL)
return;
else if (x < t->element)
remove(x, t->left);
else if (x > t->element)
remove(x, t->right);
else if (t->left != NULL && t->right != NULL) //two childen
{
t->element = findMin(t->right)->element;
remove(t->element, t->right);
}
else//single child
{
BinaryNode *oldNode = t;
t = (t->left != NULL) ? t->left : t->right;
delete oldNode;
}
}
//析构函数
template<typename Comparable>
BinarySearchTree<Comparable>::~BinarySearchTree()
{
makeEmpty();
}
template<typename Comparable>
void BinarySearchTree<Comparable>::makeEmpty()
{
makeEmpty(root);
}
template<typename Comparable>
void BinarySearchTree<Comparable>::makeEmpty(BinaryNode * & t)
{
if (t != NULL)
{
makeEmpty(t->left);
makeEmpty(t->right);
delete t;
}
t = NULL;
}
template<typename Comparable>
const BinarySearchTree<Comparable> & BinarySearchTree<Comparable>::operator=(const BinarySearchTree & rhs)
{
/*if (this != &rhs)
{
makeEmpty();
root = clone(rhs.root);
}*/
auto copy = rhs;
std::swap(*this, copy);
return *this;
}
template<typename Comparable>
typename BinarySearchTree<Comparable>::BinaryNode * BinarySearchTree<Comparable>::clone(BinaryNode *t) const
{
if (t == NULL)
return NULL;
return new BinaryNode(t->element, clone(t->left), clone(t->right));
}
//判断树是否为空
template<typename Comparable>
bool BinarySearchTree<Comparable>::isEmpty() const
{
if (root == nullptr)
return true;
else
return false;
}
//中序遍历
template<typename Comparable>
void BinarySearchTree<Comparable>::printTree(ostream & out = cout) const
{
if (isEmpty())
out << "Tree is empty" << endl;
else
printTree(root, out);
}
template<typename Comparable>
void BinarySearchTree<Comparable>::printTree(BinaryNode * t, ostream & out = cout) const
{
if (t != NULL)
{
printTree(t->left, out);
out << t->element << " ";
printTree(t->right, out);
}
}
#endif#include<iostream>
#include"BinarySearchTree.h"
using namespace std;
int main()
{
BinarySearchTree<int> t;
int NUMS = 400000;
const int GAP = 3711;
int i;
cout << "Checking... (no more output means success)" << endl;
for (i = 0; i != 100; i++)
t.insert(i);
t.printTree();
for (i = 1; i < 100; i += 2)
t.remove(i);
cout << endl;
t.printTree();
cout << "Min = " << t.findMin() << endl;
cout << "Max = " << t.findMax() << endl;
for (i = 2; i < 100; i += 2)
if (!t.contains(i))
cout << i <<"Find error1!" << endl;
BinarySearchTree<int> t2;
t2 = t;
t2.printTree();
cout << "Finished testing" << endl;
system("pause");
return 0;
}
运行结果:
Checking... (no more output means success)
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22
23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42
43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62
63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82
83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99
0 2 4 6 8 10 12 14 16 18 20 22 24 26 28 30 32 34 36 38 40 4
2 44 46 48 50 52 54 56 58 60 62 64 66 68 70 72 74 76 78 80 8
2 84 86 88 90 92 94 96 98 Min = 0
Max = 98
0 2 4 6 8 10 12 14 16 18 20 22 24 26 28 30 32 34 36 38 40 4
2 44 46 48 50 52 54 56 58 60 62 64 66 68 70 72 74 76 78 80 8
2 84 86 88 90 92 94 96 98 Finished testing
请按任意键继续. . .
课本源代码:
#ifndef BINARY_SEARCH_TREE_H
#define BINARY_SEARCH_TREE_H
#include "dsexceptions.h"
#include <algorithm>
using namespace std;
// BinarySearchTree class
//
// CONSTRUCTION: zero parameter
//
// ******************PUBLIC OPERATIONS*********************
// void insert( x ) --> Insert x
// void remove( x ) --> Remove x
// bool contains( x ) --> Return true if x is present
// Comparable findMin( ) --> Return smallest item
// Comparable findMax( ) --> Return largest item
// boolean isEmpty( ) --> Return true if empty; else false
// void makeEmpty( ) --> Remove all items
// void printTree( ) --> Print tree in sorted order
// ******************ERRORS********************************
// Throws UnderflowException as warranted
template <typename Comparable>
class BinarySearchTree
{
public:
BinarySearchTree( ) : root{ nullptr }
{
}
/**
* Copy constructor
*/
BinarySearchTree( const BinarySearchTree & rhs ) : root{ nullptr }
{
root = clone( rhs.root );
}
/**
* Move constructor
*/
BinarySearchTree( BinarySearchTree && rhs ) : root{ rhs.root }
{
rhs.root = nullptr;
}
/**
* Destructor for the tree
*/
~BinarySearchTree( )
{
makeEmpty( );
}
/**
* Copy assignment
*/
BinarySearchTree & operator=( const BinarySearchTree & rhs )
{
BinarySearchTree copy = rhs;
std::swap( *this, copy );
return *this;
}
/**
* Move assignment
*/
BinarySearchTree & operator=( BinarySearchTree && rhs )
{
std::swap( root, rhs.root );
return *this;
}
/**
* Find the smallest item in the tree.
* Throw UnderflowException if empty.
*/
const Comparable & findMin( ) const
{
if( isEmpty( ) )
throw UnderflowException{ };
return findMin( root )->element;
}
/**
* Find the largest item in the tree.
* Throw UnderflowException if empty.
*/
const Comparable & findMax( ) const
{
if( isEmpty( ) )
throw UnderflowException{ };
return findMax( root )->element;
}
/**
* Returns true if x is found in the tree.
*/
bool contains( const Comparable & x ) const
{
return contains( x, root );
}
/**
* Test if the tree is logically empty.
* Return true if empty, false otherwise.
*/
bool isEmpty( ) const
{
return root == nullptr;
}
/**
* Print the tree contents in sorted order.
*/
void printTree( ostream & out = cout ) const
{
if( isEmpty( ) )
out << "Empty tree" << endl;
else
printTree( root, out );
}
/**
* Make the tree logically empty.
*/
void makeEmpty( )
{
makeEmpty( root );
}
/**
* Insert x into the tree; duplicates are ignored.
*/
void insert( const Comparable & x )
{
insert( x, root );
}
/**
* Insert x into the tree; duplicates are ignored.
*/
void insert( Comparable && x )
{
insert( std::move( x ), root );
}
/**
* Remove x from the tree. Nothing is done if x is not found.
*/
void remove( const Comparable & x )
{
remove( x, root );
}
private:
struct BinaryNode
{
Comparable element;
BinaryNode *left;
BinaryNode *right;
BinaryNode( const Comparable & theElement, BinaryNode *lt, BinaryNode *rt )
: element{ theElement }, left{ lt }, right{ rt } { }
BinaryNode( Comparable && theElement, BinaryNode *lt, BinaryNode *rt )
: element{ std::move( theElement ) }, left{ lt }, right{ rt } { }
};
BinaryNode *root;
/**
* Internal method to insert into a subtree.
* x is the item to insert.
* t is the node that roots the subtree.
* Set the new root of the subtree.
*/
void insert( const Comparable & x, BinaryNode * & t )
{
if( t == nullptr )
t = new BinaryNode{ x, nullptr, nullptr };
else if( x < t->element )
insert( x, t->left );
else if( t->element < x )
insert( x, t->right );
else
; // Duplicate; do nothing
}
/**
* Internal method to insert into a subtree.
* x is the item to insert.
* t is the node that roots the subtree.
* Set the new root of the subtree.
*/
void insert( Comparable && x, BinaryNode * & t )
{
if( t == nullptr )
t = new BinaryNode{ std::move( x ), nullptr, nullptr };
else if( x < t->element )
insert( std::move( x ), t->left );
else if( t->element < x )
insert( std::move( x ), t->right );
else
; // Duplicate; do nothing
}
/**
* Internal method to remove from a subtree.
* x is the item to remove.
* t is the node that roots the subtree.
* Set the new root of the subtree.
*/
void remove( const Comparable & x, BinaryNode * & t )
{
if( t == nullptr )
return; // Item not found; do nothing
if( x < t->element )
remove( x, t->left );
else if( t->element < x )
remove( x, t->right );
else if( t->left != nullptr && t->right != nullptr ) // Two children
{
t->element = findMin( t->right )->element;
remove( t->element, t->right );
}
else
{
BinaryNode *oldNode = t;
t = ( t->left != nullptr ) ? t->left : t->right;
delete oldNode;
}
}
/**
* Internal method to find the smallest item in a subtree t.
* Return node containing the smallest item.
*/
BinaryNode * findMin( BinaryNode *t ) const
{
if( t == nullptr )
return nullptr;
if( t->left == nullptr )
return t;
return findMin( t->left );
}
/**
* Internal method to find the largest item in a subtree t.
* Return node containing the largest item.
*/
BinaryNode * findMax( BinaryNode *t ) const
{
if( t != nullptr )
while( t->right != nullptr )
t = t->right;
return t;
}
/**
* Internal method to test if an item is in a subtree.
* x is item to search for.
* t is the node that roots the subtree.
*/
bool contains( const Comparable & x, BinaryNode *t ) const
{
if( t == nullptr )
return false;
else if( x < t->element )
return contains( x, t->left );
else if( t->element < x )
return contains( x, t->right );
else
return true; // Match
}
/****** NONRECURSIVE VERSION*************************
bool contains( const Comparable & x, BinaryNode *t ) const
{
while( t != nullptr )
if( x < t->element )
t = t->left;
else if( t->element < x )
t = t->right;
else
return true; // Match
return false; // No match
}
*****************************************************/
/**
* Internal method to make subtree empty.
*/
void makeEmpty( BinaryNode * & t )
{
if( t != nullptr )
{
makeEmpty( t->left );
makeEmpty( t->right );
delete t;
}
t = nullptr;
}
/**
* Internal method to print a subtree rooted at t in sorted order.
*/
void printTree( BinaryNode *t, ostream & out ) const
{
if( t != nullptr )
{
printTree( t->left, out );
out << t->element << endl;
printTree( t->right, out );
}
}
/**
* Internal method to clone subtree.
*/
BinaryNode * clone( BinaryNode *t ) const
{
if( t == nullptr )
return nullptr;
else
return new BinaryNode{ t->element, clone( t->left ), clone( t->right ) };
}
};
#endif






















 1658
1658

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








