分治法思想
(1)Divide,把问题分解成子问题。
(2)Conquer,递归地解决子问题。
(3)Combine,合并子问题的解得到原问题的解。
1.归并排序
Step1:Devide——将待排序的序列分成两个子序列
Step2:Conquer——(递归地)对每个子序列进行排序
Step3:Combine——将排序好的子序列合并
T(n)=2*T(n/2)+O(n)=Θ(nlogn)
代码如下:
//合并已有序的a[p,...,q]数组和a[q+1,...,r]数组
void Merge(int a[],int p,int q,int r) {
//len1=a[p,...,q]数组长度;len2=a[q+1,...,r]数组长度
int len1 = q-p+1;
int len2 = r-q;
//为a[p,...,q],a[q+1,...,r]的临时数组L,R赋值
int L[len1],R[len2];
for(int i = 0;i<len1;i++)
L[i] = a[p+i];
for(int j =0;j<len2;j++)
R[j] = a[q+j+1];
int i=0,j=0,k=0;
//比较L,R两个待合并数组的值,将较小的值插入原数组中
//直到L或R数组访问完最后一个元素
while(i<len1 && j<len2) {
if(L[i]<R[j]) {
a[p+k]=L[i];
i++;
}
else {
a[p+k]=R[j];
j++;
}
k++;
}
//如果L数组没到达尾部
while(i<len1) {
a[p+k] = L[i];
i++;
k++;
}
//如果R数组没到达尾部
while(j<len2) {
a[p+k] = R[j];
j++;
k++;
}
}
//归并排序
void MergeSort(int a[],int low,int high) {
//如果待合并的数组长度为1,返回
int length = high-low+1;
if(length == 1)
return;
int mid = (low+high)/2;
MergeSort(a,low,mid);
MergeSort(a,mid+1,high);
Merge(a,low,mid,high);
}
2.二分查找
Step1:Devide——将x与序列的中间元素比较
Step2:Conquer——(递归地)在子有序数列中查找x
Step3:Combine——nothing
T(n)=1*T(n/2)+O(1)=Θ(logn)
代码如下:
int BinarySearch(int a[], int low, int high, int expected) {
if (low > high)
return -1;
int mid = (low + high) / 2;
if (a[mid] == expected)
return mid;
if (a[mid] < expected)
return BinarySearch(a, mid + 1, high, expected);
else
return BinarySearch(a, low, mid - 1, expected);
}
3.幂次方问题 (Powering a Num)

T(n)=T(n/2)+O(1)=Θ(logn)
代码如下:
int Power(int x, int n) {
if (n == 0)
return 1;
if (n == 1)
return x;
int t = Power(x, n / 2);
if (n & 0x01 == 1)
return t * t * x;
else
return t * t;
}
4.Fibonacci数列-平方递归法
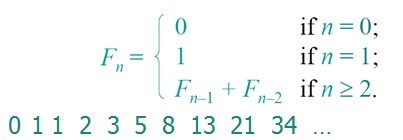
归纳法得
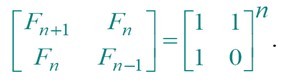
2维方阵,计算过程中矩阵形式保持不变,而且二维方阵乘法是常数时间操作,
因此,该算法的时间复杂度与计算x^n类似,为:Θ(logn)
代码如下:
struct Matrix{
int data[2][2];
};
Matrix Mutiply(const Matrix& a, const Matrix& b) {
Matrix c;
for(int i=0;i<2;i++) {
for(int j=0;j<2;j++) {
c.data[i][j] = 0;
for (int k = 0; k < 2; k++)
c.data[i][j] += a.data[i][k] * b.data[k][j];
}
}
return c;
}
Matrix MatrixOprate(int n) {
Matrix m;
int data[2][2] = {{1,1},{1,0}};
for(int i=0;i<2;i++)
for(int j=0;j<2;j++)
m.data[i][j] = data[i][j];
if (n == 1)
return m;
Matrix t = MatrixOprate(n/2);
if(n & 0x01 == 1)
return Mutiply(Mutiply(t,t),m);
else
return Mutiply(t,t);
}
int Fibonacci(int n) {
if (n <= 0)
return 0;
if (n == 1)
return 1;
Matrix m = MatrixOprate(n-1);
return m.data[0][0];
}
5.矩阵乘积
5.1一般的矩阵乘法算法
若A为m×n矩阵,B为n×p矩阵,则他们的乘积AB会是一个m×p矩阵。其乘积矩阵的元素如下面式子得出:
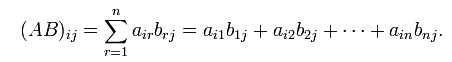
显然,时间复杂度Θ(n)=n^3
代码如下:
const int MAXN=1000;
struct matrix{
int n, m;
double data[MAXN][MAXN];
};
int multiply(matrix& c, const matrix& a, const matrix& b){
if (a.m != b.n)
return 0;
c.n = a.n;
c.m = b.m;
for (int i = 0; i < c.n; i++)
for (int j = 0; j < c.m; j++) {
c.data[i][j] = 0;
for (int k = 0; k < a.m; k++)
c.data[i][j] += a.data[i][k] * b.data[k][j];
}
return 1;
}
5.2 矩阵分块,实现分治
原理如下图所示:
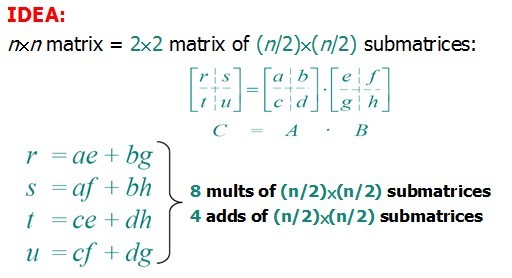
T(n)=8*T(n/2)+Θ(n^2),使用主定理求得Θ(n)=n^3,并没有什么卵用。
5.3斯特拉森算法,绝对的牛逼闪闪
考虑对T(n)=8*T(n/2)+Θ(n^2)这个递归式进行优化,显然,Θ(n^2)对应于矩阵的加法操作,并不能很好地优化,所以对8T(n/2)j进行优化,要么让8变小,要么让2变大,以使得n^logab小于3。
而牛逼闪闪的斯特拉森就是推导出一套新的公式,使得8->7,实现了时间复杂度的优化,使其变为O(n^log2 7)约等于O(n^2.81)。

代码略,(,,• ₃ •,,)(,,• ₃ •,,)(,,• ₃ •,,)









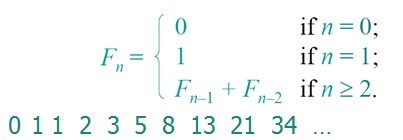
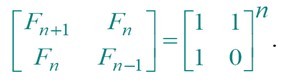
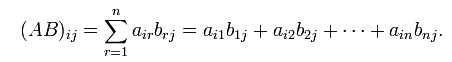
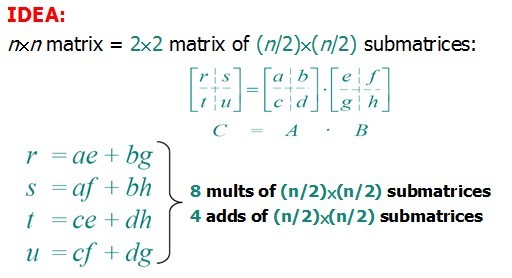
















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








