谱聚类基础-原理和细节（2）：实践中的选择细节I

上回书说到，谱聚类算法实现的过程中有许多参数需要选择。今天就想具体地谈谈这些参数选择的“规矩”。

首先，回顾一下上一篇文章中的一部分内容

讨论范围为三种不同的谱聚类算法：

1. unnormalized spectral clustering
2. Shi and Malik的算法（2000）
3. NJW算法（2002）

其中算法1使用未标准化Laplacian矩阵，算法2，3则分别使用了不同的标准化Laplacian矩阵。
（算法2使用的Laplacian为$L_{rw}$，算法3使用的Laplacian矩阵为$L_{sym}$，关于Laplacian矩阵，本文中将会给予具体的说明）
把他们分别称为非标准化谱聚类和标准化谱聚类。

假设需要聚类的$n$个点$x_{1},x_{2},...,x_{n}$（通常考虑这些点在$R$上的某个向量空间中）
谱聚类算法的实施过程通常包含以下几个步骤：
1.输入：相似度矩阵$S$（$R_{n*n}$）、目标聚类数目$k$
（在此之前需要完成两项工作： 1.选择合适的相似度函数，2.选择合适的聚类数目$k$）
2.构造出相似图及其赋权的邻接矩阵（weighted adjacency matrix）
（这一步需要选择：相似图的类型以及相应的参数）
3.计算出相似图的$Laplacian$矩阵
（这一步需要选择：$Laplacian$矩阵的类型）
4.计算$Laplacian$矩阵的前$k$个特征值对应的特征向量，以这$k$个特征向量为列，拼出新的矩阵$U_{n*k}）$
5.视矩阵U的每一行为$R_{k}$中的一个点，对这$n$个点$y_{1}，y_{2}，...y_{n}$进行$k-means$聚类，得到$k$个聚类$C_{1}，C_{2}，...C_{k}$
6.输出聚类结果$A_{1},A_{2},...A_{k}$：$y_{i}$被分到$C_{j}$中的哪一类，$x_{i}$就被分到相应的$A_{j}$类

可以看到，在谱聚类算法的实施中，有着诸多需要人为控制的地方。其中，选择的不同可能导致不同类型的谱聚类算法（Laplacian矩阵的选择），另外的一些选择则没有涉及算法框架的不同（相似度函数、聚类数目k、相似图的类型和参数）。

关于这些所有的选择，都有一定的经验规则，也即是本文主要讨论的内容。

本文将分为以下几个部分：

* 相似度函数的选择
* 相似图类型、参数的选择
* 聚类数目的选择
* Laplacian矩阵的选择
* k-means步骤的其他可能性
* 关于特征向量计算的说明

正文开始：

相似度函数的选择

这是一个很困难的问题，至少我觉得如此。现在大家都在用的相似度函数都是高斯相似度函数（Gaussian similarity function）：

$s(x_{i},x_{j})=exp(-\left \| x_{i}-x_{j} \right \|/(2\sigma^{2}))$
当然，这里有一个潜在的假设：数据点都处于欧式空间 $R^{d}$中。注意到，这里有一个参数 $\sigma$是需要选取的，我们将在稍后的 相似图类型、参数的选择中谈到。

但真的如我们所见如此，都只使用上述的高斯相似度函数吗？如果可以的话，我还是乐于见到有其他备选项的。我觉得真的很难让人相信，这样一个简单的式子，就能把所有的相似的数据点之间的特征描述清楚的。

从理论上来说，选择不同的相似度函数还是可能的。而设计相似度函数时，有两点是值得注意的
1.有意义：即根据相似度函数判断的非常类似的数据点，在数据的应用背景中，也应该是非常相似的。
2.”微观效应”不那么重要：数据点之间的相似度是0.01还是0.001，带来的影响并不大，因为这些值已经足够小，在相似图中，我们是不会把这样的点连起来的（相信看到后文相似图类型、参数的选择部分，会有更直观的了解）。

很遗憾，关于相似度函数的选择，我能说的只有这么些了。希望以后能有对于“相似”更为本质的认识，可以谈得远一些。

相似图类型、参数的选择

相似图的构造是谱聚类中非常重要的一步，得到它的赋权邻接矩阵$W$，是计算Laplacian矩阵的起点。关注相似图构造中需要注意的一些事项，也因此成为了实践中考虑的重点。

在相似图的构造阶段，对于数据集$x_1,...,x_n$，已经知道了点之间的相似度$s_{ij}$或者点之间的距离$d_{ij}$，要把它们放到以$n$个数据点为顶点(在图中，把这些顶点依次记为$v_1,...,v_n$)的图中，以连接顶点的边的形式表示出来。

在这一部分，我们首先来了解一下相似图的几种类型：
1.$\epsilon$-邻图(The ε -neighborhood graph)
选定参数$\epsilon$，把点间距离小于$\epsilon$的点连接起来，所得到的图就是$\epsilon$-邻图。
在$\epsilon$-邻图中，所有被连接起来的点之间的距离几乎都有着差不多的大小（至多为$\epsilon$），因此常常会出现这样的情况：即使给这些连起来的边赋权，也并不能把数据中的更多信息体现到图里来。所以，在一般情况下，$\epsilon$-邻图都视作无权图(unweighted graph)考虑。

2.$k$-近邻图(k-nearest neighbor graph)
选定参数$k$，对于顶点$v_i,i=1,..,n$，把离它最近的$k$个点与之相连，所得到的图就是$k$-近邻图。
需要注意的是，因为这样的邻近关系并不是对称的($v_j$是$v_i$的$k$近邻 $\neq v_i$是$v_j$的$k$近邻)，故而得到的图将会是“有向”的。为了得到无向的图（图的赋权邻接矩阵$W$应是对称的），一般采取的办法有两种：
(1)忽视边的方向。即只要$v_j$是$v_i$的$k$近邻，或者$v_i$是$v_j$的$k$近邻，就用一条无向边把$v_i$与$v_j$连接起来。通常称的$k$-近邻图就是这一种。
(2)仅当$v_j$是$v_i$的$k$近邻，且$v_i$是$v_j$的$k$近邻时，才把$v_i$与$v_j$连接起来。这样得到的图称为混合$k$-近邻图(mutual k-nearest neighbor graph)

3.全连通图(The fully connected graph)
在这里，只是把所有具有非负相似度的点都连接起来，并以其之间的相似度$s_{ij}$作为边的权值。
我们期望得到的图能够很好地表达局部邻域信息，因此仅当相似度函数本身就能很好地模拟局部邻域时，全连通的图才是好的选择。一个很普遍的例子就是利用前面提到的高斯相似度函数来构造这样的全连通图，此时函数中的参数$\sigma$起到的作用就是控制邻域的宽度，它与$\epsilon$在$\epsilon$-邻图中起到的作用类似。

以上的几种都是在谱聚类中常用的相似图。就我们目前所知，关于这些相似图的选择，还没有好的理论结果。
接下来，我们将谈谈在实际应用中，这些图的表现和选择

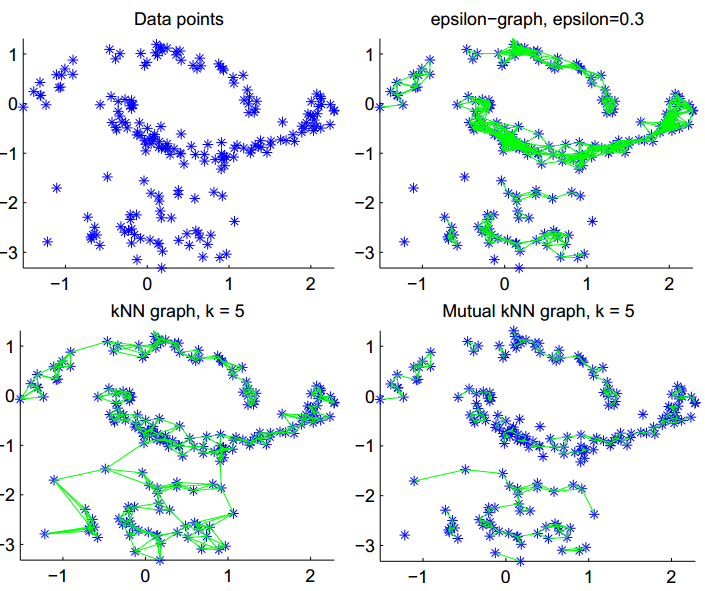
上图为测试数据，以说明各图之特点。（图由两个”月亮”和一个依高斯分布取样的散点集组成，其中下面的“月亮”较之上方，点的密度大一些）

1.$\epsilon$-邻图(The ε -neighborhood graph)
有效的参数$\epsilon$并不好选择。在上图（右上）中，可以看到中间的”月亮”中的点都被紧密地连接起来了，但对于取自高斯分布的点，效果却不太好。事实上正是如此，$\epsilon$-邻图难以处理多尺度（即不同区域内，点之间的距离也不相同）的数据。

2.$k$-近邻图(k-nearest neighbor graph)
相较而言，$k$-近邻图可以把具有不同尺度的区域中的点连接起来，这有时是很好的性质。在上图（左下）中就能看到，低密度的高斯分布样本点与中间的月亮之间连接起来了。 同样，可以看到，当两个高密度的区域相距得足够远时，将会被分为两个连通分支，左下图中的两个月亮即是此例。

3.混合$k$-近邻图(mutual k-nearest neighbor graph)
它倾向于把某一固定密度的区域内的点连接起来，而不是把具有不同密度的区域之间的点相连。因此，看上去它可以是$\epsilon$-邻图与$k$-近邻图的一个折中的选择：既能处理多尺度的数据，又不会把不同密度的区域相互混淆。当希望得到不同密度的聚类时，将会是很好的选择。

4.全连通图(The fully connected graph)
正如刚才提到的一样，参数$\sigma$在这里起到的作用，与$\epsilon$在$\epsilon$-邻图中起到的作用类似，都是控制邻域的大小。在局部邻域内的两个点的连边有着相对高的权重，但相距远的点之间的连边的权值则是几乎可以忽略的。并且，使用全连通图时，得到的赋权邻接矩阵不是稀疏的，可能会为计算带来一些负担。

在实践中，一般建议采取$k$-近邻图(k-nearest neighbor graph)作为第一选择：它能够被简单地构造、得到的赋权邻接矩阵是稀疏的、对于参数的稳定性也较其他图好一些。

这一部分的最后，来看看不同类型图的参数选取的一些经验规则。

遗憾的是，几乎没有理论上的结果来指导这一任务。
一般而言，如果相似图中包含着比算法要求的聚类数目更多的连通分支，谱聚类算法将会平凡地将连通分支作为聚类返回。除非操作者能保证这些连通分支就是正确的聚类，否则是应该尽量使得相似图是全连通的，或者只包含几个很少的连通分支（或孤立点）。
其实在随机图的连通性上，还是有许多理论上的结果的，但所有的这些结果都是渐进（即数据点的个数$n$趋近于无穷）情况下成立的。比如说具有$R^d$中连通支撑的$n$个独立同分布（假设某背景分布）的数据点，当$k$的取值大小与$log(n)$相当时，k近邻图和混合k近邻图将会是连通的；类似的结果也在$\epsilon$-邻图的情况下存在：如果选取$\epsilon$的大小为$(log(n)/n)^d$时，能保证图的连通性。这些理论结果因其假设条件的限制，在实际应用（样本总是有限的）中几乎不能帮助我们选择更好的参数。
所以关注经验规则其实也是非常无奈的选择。现在就来看看吧。

1.$\epsilon$-邻图(The ε -neighborhood graph)
计算使得图保持连通的$\epsilon$的最小值还是比较简单的，它正好等于全连通图的最小生成树中最长边的长度，通过最小生成树算法即可计算。但如果数据中存在离群点，选出的$\epsilon$就会很大，因为也要保证离群点被连入图中。此外，如果图中出现相互远离的小聚类的时候，也会出现类似的问题。这些情况下，对于反应数据中最重要的信息来说，$\epsilon$都取得太大了。

2.$k$-近邻图(k-nearest neighbor graph)
对于中等大小的图，可以通过手试的办法来确定$k$；而对于非常大的图/样本，则可以依照刚才提到的结果来选择k,即规模要大致在$log(n)$。

3.混合$k$-近邻图(mutual k-nearest neighbor graph)
可以发现，当$k$值取定时，混合$k$-近邻图较$k$-近邻图的边要少得多。因此建议使用混合$k$-近邻图时，可以选择相比使用$k$-近邻图时更大一些的$k$值。此外，利用混合$k$-近邻图不易把密度不同的区域连接起来的特点，有时可以允许一些“有意义”的不连通分支出现。但我们无法给出更为一般的关于$k$选取的建议。

4.全连通图(The fully connected graph)
使用全连通图时，有一个需求，就是对于每一个点来说，与它的相似度显著地大于$0$的顶点应该既不太多也不太少。特别地，选取高斯相似度函数时，有一些经验可以参考。(1)取$\sigma$的大小规模为在$k$-近邻图中，第$k$个最近邻顶点的平均距离(这里$k$的大小按照$log(n)$的规模选取)；(2)通过最小生成树算法算出前面提到的$\epsilon$，再取$\sigma=\epsilon$。

但要注意的是，上面的所有经验法则都只是经验法则而已，面对具体的数据，它们可能失效，参数的选择就要看使用者的敏锐了。

就先谈这么些吧，由于篇幅过长，后面的内容包括：聚类数目的选择、 Laplacian矩阵的选择、k-means步骤的其他可能性、关于特征向量计算的说明将另开一篇续之。