这组文章作为读完Ulrike von Luxburg的论文
A Tutorial on Spectral Clustering(2007)的一个总结。
论文的讨论范围为三种不同的谱聚类算法:
1. unnormalized spectral clustering
2. Shi and Malik的算法(2000)
3. NJW算法(2002)
其中算法1使用**未经过标准化的**Laplacian矩阵,
算法2,3则分别使用了不同的**经过标准化的**Laplacian矩阵(算法2使用的Laplacian为L_rw,算法3使用的Laplacian矩阵为L_sym)。
把他们分别称为非标准化谱聚类和标准化谱聚类。
假设需要聚类的
n
个点
谱聚类算法的实施过程通常包含以下几个步骤:
1.输入:相似度矩阵
(在此之前需要完成两项工作: 1.选择合适的相似度函数,2.选择合适的聚类数目
2.构造出相似图及其赋权的邻接矩阵(weighted adjacency matrix)
(这一步需要选择:相似图的类型以及相应的参数)
3.计算出相似图的
Laplacian
矩阵
(这一步需要选择:
Laplacian
矩阵的类型)
4.计算
Laplacian
矩阵的前
k
个特征值对应的特征向量,以这
5.视矩阵U的每一行为
Rk
中的一个点,对这
n
个点
6.输出聚类结果
A1,A2,...Ak
:
yi
被分到
Cj
中的哪一类,
xi
就被分到相应的
Aj
类
可以看到,在谱聚类算法的实施中,有着诸多需要人为控制的地方。其中,选择的不同可能导致不同类型的谱聚类算法( Laplacian 矩阵的选择),另外的一些选择则没有涉及算法框架的不同(相似度函数、聚类数目k、相似图的类型和参数)。而关于这些所有的选择,都有一定的经验规则 [实在是没有办法,完备理论上的支持几乎没有]。这些经验规则,将在下一篇博文里总结,这里先不讨论。
转回正题,论文从以下三个角度来分别讨论了谱聚类算法的原理:
* 图的划分(graph cut)
* 随机行走(random walk)
* 矩阵的扰动理论(perturbation theory)
作为关于谱聚类算法的第一篇总结,本文先从图划分观点来解释一下谱聚类算法的原理。
图划分观点
在前面的算法部分,我们知道,相似的概念起着重要的作用。而直观上来看,聚类问题就是根据相似度,把点分到不同的群组里。如果我们已经知道数据的相似图,那么这个问题事实上是:要找到一个图的划分,使得连接不同群组的边的权重尽可能小(意味着不同类中的点之间是不同的),而在群组内部的边有着很高的权重(意味着相同类中的点是彼此相似的)。这一问题的解决并不容易,而谱聚类算法事实上解决了这一问题的一个放松形式。
已知一个图的邻接矩阵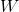
其中
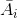 代表图中除
代表图中除
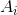 以外的点(称为
以外的点(称为
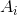 的补),
的补),
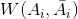 代表连接
代表连接
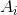 与
与
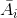 间点的所有边的权值之和,引入系数
1/2
则是为了削减重复计算。
间点的所有边的权值之和,引入系数
1/2
则是为了削减重复计算。
在实现中,上述的 mincut 问题的解决可以是很高效的,但其给出的解作为聚类的结果,常常却非常不理想。一个严重的问题就是,很容易得到单独的点作为一个类。这显然是我们不乐于见到的。
于是我们想办法改善
mincut
的情况,最常见的两种新的目标函数诞生了:
RatioCut
和
Ncut
。引入这两个目标函数的动机很简单:控制每个聚类中点的数目都在比较大的水平上。但为了实现这一动机,它们采取的手段还是有着细小的区别。
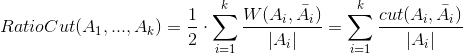
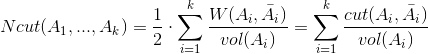
其中
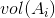 代表聚类
Ai
中所有边的权值和。
代表聚类
Ai
中所有边的权值和。
可以看到,在
RatioCut
中,通过除掉聚类中的顶点数来控制聚类的大小;而在
Ncut
中,则通过除掉聚类中边的权值和来控制聚类的大小。这样的方法确实能够起到作用,为说明这一点,只需注意到式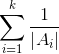
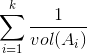
现在的情况看起来很不错,只需要解决
RatioCut
或者
Ncut
就好了,可往下走的话,问题就出现了:原来的
mincut
是可以高效解的;而要最小化
RatioCut
和
Ncut
,却是
NP
难!
我们再也无法像以前解决
mincut
问题一样简单地解决它了。
这当然抵挡不了学者们执着的心,即使看起来堵死的路,也要把它走出来。
于是一条看起来很自然的路子出现了:把最小化
RatioCut
和
Ncut
的条件进行放松,以达到可以快速求解的目的。
但是,在这之前,为了看清楚问题的本来面目,我们需要转换一下它的表述形式。
(待会儿可以看到,当我们开始放松条件时,谱聚类算法作为这一问题的一种解决方案开始浮出水面)
现在,以
RatioCut
和 聚类数目
k=2
为例,来解释这个问题。
此时,我们的目标是求解最优化问题:
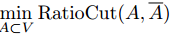
假如我们定义一个向量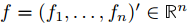
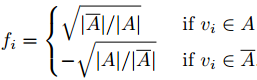 (1)
(1)
那么神奇的事情出现了:目标函数
RatioCut
可以通过非标准化
Laplacian
矩阵
L
表示出来。具体如下:
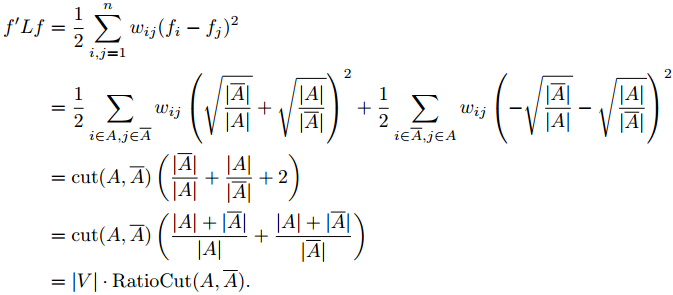
又由于向量
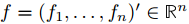 满足如下性质:
满足如下性质: (1)与常向量1正交,即
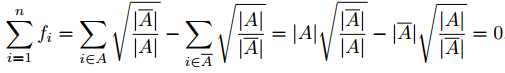
(2)范数的平方等于n,即
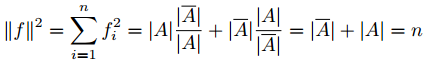
因此,最小化
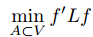 ,满足
f
与常向量
,满足
f
与常向量这是一个离散优化问题,因为解向量 f 的元素只能取两个特定的值。
当然这个问题仍然是NP难的。
关键的时刻到了,我们要对这个问题上面的形式进行放松:把离散的情形转化成连续的情形:
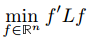 ,满足
,满足现在终于可以快速地解决这一问题了。
通过
Rayleigh−Ritz
定理,我们知道,非标准化的
Laplacian
阵
L
的第二小特征值对应的特征向量正是在上述放松形式下,所要求的向量(注意到L的最小特征值为
所以,通过给出矩阵
然而,为了得到图的一个划分,还需要对求得的向量
f
进行一定的变换,使得它能指明每个点所属的聚类。
最简单的方法是按照下面的规则来对图进行划分:
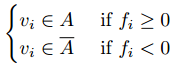
不过这不是目标聚类数目
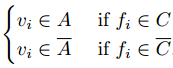
来对图进行划分。
现在已经不难发现,这不就是谱聚类的方法吗?
计算
Laplacian
阵的特征向量,再对它们进行聚类,按照聚类结果进行图的划分。
终于,在她的身后拍了拍肩膀,等她转过来,发现真的是要找的人。
(本节完)






















 8049
8049

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








