牛顿法

平时经常看到牛顿法怎样怎样，一直不得要领，今天下午查了一下维基百科，写写我的认识，很多地方是直观理解，并没有严谨的证明。在我看来，牛顿法至少有两个应用方向，1、求方程的根，2、最优化。牛顿法涉及到方程求导，下面的讨论均是在连续可微的前提下讨论。

 

1、求解方程。

并不是所有的方程都有求根公式，或者求根公式很复杂，导致求解困难。利用牛顿法，可以迭代求解。

原理是利用泰勒公式，在x0处展开，且展开到一阶，即f(x) = f(x0)+(x－x0)f'(x0)

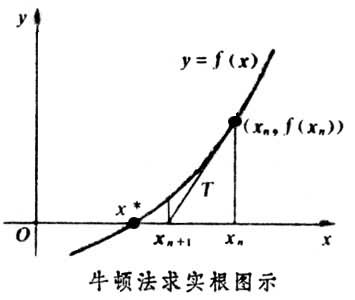
求解方程f(x)=0，即f(x0)+(x-x0)*f'(x0)=0，求解x = x1=x0－f(x0)/f'(x0)，因为这是利用泰勒公式的一阶展开，f(x) = f(x0)+(x－x0)f'(x0)处并不是完全相等，而是近似相等，这里求得的x1并不能让f（x）=0，只能说f(x1)的值比f(x0)更接近f（x）=0，于是乎，迭代求解的想法就很自然了，可以进而推出x(n+1)=x(n)－f(x(n))/f'(x(n))，通过迭代，这个式子必然在f（x*）=0的时候收敛。整个过程如下图：

 

2、牛顿法用于最优化

在最优化的问题中，线性最优化至少可以使用单纯行法求解，但对于非线性优化问题，牛顿法提供了一种求解的办法。假设任务是优化一个目标函数f，求函数f的极大极小问题，可以转化为求解函数f的导数f'=0的问题，这样求可以把优化问题看成方程求解问题（f'=0）。剩下的问题就和第一部分提到的牛顿法求解很相似了。

这次为了求解f'=0的根，把f（x）的泰勒展开，展开到2阶形式：

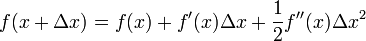
这个式子是成立的，当且仅当 Δx 无线趋近于0。此时上式等价与：

 (原因是当Δx 趋近于0的时候f(x)=f(x+Δx )所以才有： )

求解：

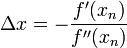
得出迭代公式：

一般认为牛顿法可以利用到曲线本身的信息，比梯度下降法更容易收敛（迭代更少次数），如下图是一个最小化一个目标方程的例子，红色曲线是利用牛顿法迭代求解，绿色曲线是利用梯度下降法求解。

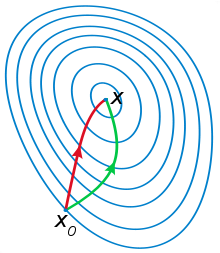
在上面讨论的是2维情况，高维情况的牛顿迭代公式是：

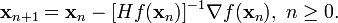
其中H是hessian矩阵，定义为：

 

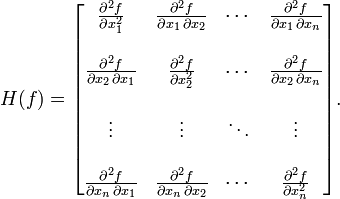
高维情况依然可以用牛顿迭代求解，但是问题是Hessian矩阵引入的复杂性，使得牛顿迭代求解的难度大大增加，但是已经有了解决这个问题的办法就是Quasi-Newton methond，不再直接计算hessian矩阵，而是每一步的时候使用梯度向量更新hessian矩阵的近似。Quasi-Newton method的详细情况我还没完全理解，且听下回分解吧。。。

牛顿法的好处在于当接近最优解的时候其收敛误差将会是上一次迭代的误差平方，例如上次 误差0.001 下次将会小于0.00001 这也就是所谓的二次收敛

参考：

牛顿法是二阶收敛，梯度下降是一阶收敛，所以牛顿法就更快。如果更通俗地说的话，比如你想找一条最短的路径走到一个盆地的最底部，梯度下降法每次只从你当前所处位置选一个坡度最大的方向走一步，牛顿法在选择方向时，不仅会考虑坡度是否够大，还会考虑你走了一步之后，坡度是否会变得更大。所以，可以说牛顿法比梯度下降法看得更远一点，能更快地走到最底部。

根据wiki上的解释，从几何上说，牛顿法就是用一个二次曲面去拟合你当前所处位置的局部曲面，而梯度下降法是用一个平面去拟合当前的局部曲面，通常情况下，二次曲面的拟合会比平面更好，所以牛顿法选择的下降路径会更符合真实的最优下降路径。

wiki上给的图很形象，我就直接转过来了：<img src="https://pic4.zhimg.com/365e99bcf8d2e1ef1986e09c795caef7_b.jpg" data-rawwidth="220" data-rawheight="253" class="content_image" width="220">红色的牛顿法的迭代路径，绿色的是梯度下降法的迭代路径。 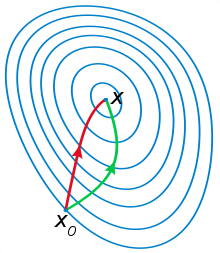红色的牛顿法的迭代路径，绿色的是梯度下降法的迭代路径。

2.指数分布族（The exponential family）

指数分布族是指可以表示为指数形式的概率分布。指数分布的形式如下：

P(y;η)=b(y)exp(ηTT(y)−a(η))

其中，η成为分布的自然参数（nature parameter）；T(y)是充分统计量（sufficient statistic），通常 T(y)=y。当参数 a、b、T 都固定的时候，就定义了一个以η为参数的函数族。

下面介绍两种分布，伯努利分布和高斯分布，分别把它们表示成指数分布族的形式。

伯努利分布

伯努利分布是对0，1问题进行建模的，对于Bernoulli（ φ ）, yϵ{0,1} .有 p(y=1;φ)=φ;p(y=0;φ)=1−φ ，下面将其推导成指数分布族形式：

 

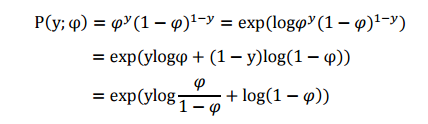
将其与指数族分布形式对比，可以看出：

 

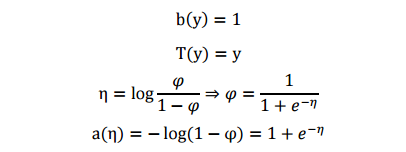
表明伯努利分布也是指数分布族的一种。从上述式子可以看到， η 的形式与logistic函数（sigmoid）一致，这是因为 logistic模型对问题的前置概率估计其实就是伯努利分布。

高斯分布

下面对高斯分布进行推导，推导公式如下（为了方便计算，我们将方差  σ 设置为1）：

 

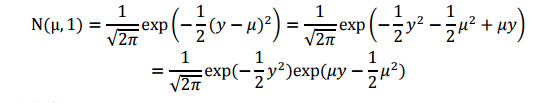
将上式与指数族分布形式比对，可知：

b(y)=12π−−√exp(−12y2)

T(y)=y

η=μ

a(η)=12μ2

两个典型的指数分布族，伯努利和高斯分布。其实大多数概率分布都可以表示成指数分布族形式，如下所示：

• 伯努利分布（Bernoulli）：对 0、1 问题进行建模；
• 多项式分布（Multinomial）：多有 K 个离散结果的事件建模；
• 泊松分布（Poisson）：对计数过程进行建模，比如网站访问量的计数问题，放射性衰变的数目，商店顾客数量等问题；
• 伽马分布（gamma）与指数分布（exponential）：对有间隔的正数进行建模，比如公交车的到站时间问题；
• β 分布：对小数建模；
• Dirichlet 分布：对概率分布进建模；
• Wishart 分布：协方差矩阵的分布；
• 高斯分布（Gaussian）；

下面来介绍下广义线性模型（Generalized Linear Model, GLM）。

3.广义线性模型（Generalized Linear Model, GLM）

你可能会问，指数分布族究竟有何用？其实我们的目的是要引出GLM，通过指数分布族引出广义线性模型。

仔细观察伯努利分布和高斯分布的指数分布族形式中的 η 变量。可以发现，在伯努利的指数分布族形式中， η 与伯努利分布的参数 φ 是一个logistic函数（下面会介绍logistic回归的推导）。此外，在高斯分布的指数分布族表示形式中， η 与正态分布的参数 μ 相等，下面会根据它推导出普通最小二乘法（Ordinary Least Squares）。通过这两个例子，我们大致可以得到一个结论， η 以不同的映射函数与其它概率分布函数中的参数发生联系，从而得到不同的模型，广义线性模型正是将指数分布族中的所有成员（每个成员正好有一个这样的联系）都作为线性模型的扩展，通过各种非线性的连接函数将线性函数映射到其他空间，从而大大扩大了线性模型可解决的问题。

下面我们看 GLM 的形式化定义，GLM 有三个假设：

• (1)  y|x;θ ExponentialFamily（η） ；给定样本 x 与参数 θ ，样本分类 y  服从指数分布族中的某个分布；
• (2) 给定一个  x ，我们需要的目标函数为 hθ(x)=E[T(y)|x] ;
• (3) η=θTx 。

依据这三个假设，我们可以推导出logistic模型与普通最小二乘模型。首先根据伯努利分布推导Logistic模型，推导过程如下:

hθ(x)=E[T(y)|x]=E[y|x]=p(y=1|x;θ)

=φ

=11+e−η

=11+e−θTx

公式第一行来自假设(2)，公式第二行通过伯努利分布计算得出，第三行通过伯努利的指数分布族表示形式得出，然后在公式第四行，根据假设三替换变量得到。

同样，可以根据高斯分布推导出普通最小二乘，如下：

hθ(x)=E(T(y)|x)=E[y|x]

=μ

=η

=θTx

公式第一行来自假设（2），第二行是通过高斯分布 y|x;θ ~ N(μ,σ2) 计算得出，第三行是通过高斯分布的指数分布族形式表示得出，第四行即为假设（3）。

其中，将η与原始概率分布中的参数联系起来的函数成为正则相应函数（canonical response function），如 φ=11+e−η、μ=η 即是正则响应函数。正则响应函数的逆成为正则关联函数（canonical link function）。

所以，对于广义线性模型，需要决策的是选用什么样的分布，当选取高斯分布时，我们就得到最小二乘模型，当选取伯努利分布时，我们得到 logistic 模型，这里所说的模型是假设函数 h 的形式。

最后总结一下：广义线性模型通过假设一个概率分布，得到不同的模型，而梯度下降和牛顿方法都是为了求取模型中的线性部分 (θTx) 的参数 θ 的。

多分类模型-Softmax Regression

下面再给出GLM的一个例子——Softmax Regression.

假设一个分类问题，y可取k个值，即 yϵ{1,2,...,k} 。现在考虑的不再是一个二分类问题，现在的类别可以是多个。如邮件分类：垃圾邮件、个人邮件、工作相关邮件。下面要介绍的是多项式分布（multinomial distribution）。

多项式分布推导出的GLM可以解决多类分类问题，是 logistic 模型的扩展。对于多项式分布中的各个y的取值，我们可以使用k个参数 ϕ1,ϕ2,...,ϕk 来表示这k个取值的概率。即

P(y=i)=ϕi

但是，这些参数可能会冗余，更正式的说可能不独立，因为 ∑ϕi=1 ，知道了前k-1个，就可以通过 1−∑k−1i=1ϕi 计算出第k个概率。所以，我们只假定前k-1个结果的概率参数 ϕ1,ϕ2,...,ϕk−1 ，第k个输出的概率通过下面的式子计算得出：

ϕk=1−∑i=1k−1ϕi

为了使多项式分布能够写成指数分布族的形式，我们首先定义 T(y)，如下所示：

 

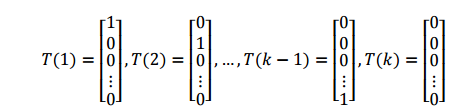
和之前的不一样，这里我们的 T(y) 不等 y ， T(y) 现在是一个 k−1 维的向量，而不是一个真实值。接下来，我们将使用 (T(y))i 表示 T(y) 的第i个元素。

下面我们引入指数函数I，使得：

I(True)=1,I(False)=0

这样， T(y) 向量中的某个元素还可以表示成：

(T(y))i=I(y=i)

举例来说，当 y=2时，T(2)2=I(2=2)=1，T(2)3=I(2=3)=0 。根据公式 15，我们还可以得到：

E[(T(y))i]=∑y=1k(T(y))ϕi=∑y=1kI(y=i)ϕi=ϕi

∑i=1kI(y=i)=1

下面，二项分布转变为指数分布族的推导如下：

 

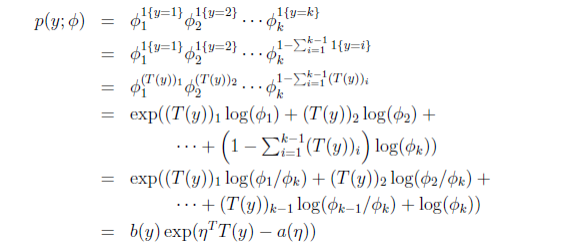
其中，最后一步的各个变量如下：

 

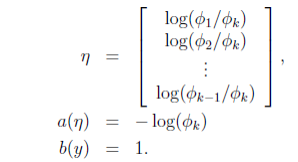
由 η 的表达式可知：

ηi=logϕiϕk⇒ϕi=ϕkeηi

为了方便，再定义：

ηk=logϕkϕk=0

于是，可以得到：

∑j=1kϕi=∑j=1kϕkeηi=1⇒ϕk=1∑kj=1eηi

将上式代入到 ηi=logϕiϕk⇒ϕi=ϕkeηi ，得到：

ϕi=eηi∑kj=1eηi=eηi1+∑k−1j=1eηi

从而，我们就得到了连接函数，有了连接函数后，就可以把多项式分布的概率表达出来:

P(y=i)=ϕi=eηi1+∑k−1j=1eηi=eθTix1+∑k−1j=1eθTjx

注意到，上式中的每个参数 ηi 都是一个可用线性向量 θTix 表示出来的，因而这里的 θ 其实是一个二维矩阵。

于是，我们可以得到假设函数 h 如下：

 

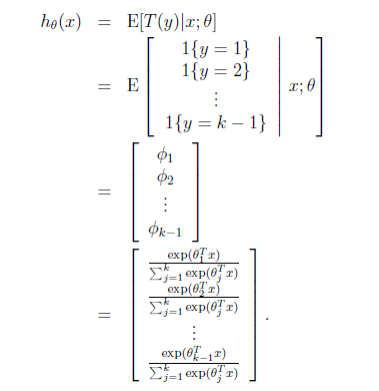
那么就建立了假设函数，最后就获得了最大似然估计

 

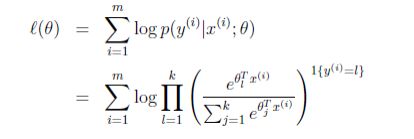
对该式子可以使用梯度下降算法或者牛顿方法求得参数 θ 后，使用假设函数 h 对新的样例进行预测，即可完成多类分类任务。这种多种分类问题的解法被称为 softmax regression.

附录：

斯坦福机器学习第4讲
附上大神笔记：

http://blog.csdn.net/dream_angel_z/article/details/46288167#t1