图

一、一些概念

图（Graph）是由顶点的有穷非空集合和顶点之间边的集合组成，通常表示为：G（V，E），其中，G表示一个图，V是图G中顶点的集合，E是图G中边的集合。

线性表中，相邻的数据元素之间具有线性关系，树结构中，相邻两层的结点具有层次关系，而图中，任意两个顶点之间都可能有关系，顶点之间的逻辑关系用边来表示，边集可以是空的。

无向边：若顶点Vi到Vj之间的边没有方向，则称这条边为无向边（Edge），用无序偶对（Vi，Vj）来表示。如果图中任意两个顶点之间的边都是无向边，则称该图为无向图（Undirected graphs）。

 

有向边：若顶点Vi到Vj的边有方向，则称这条边为有向边，也称为弧（Arc）。用有序偶对<Vi，Vj>来表示，Vi称为弧尾（Tail），Vj称为弧头（Head）。如果图中任意两个顶点之间的边都是有向边，则称该图为有向图（Directed graphs）。

有些图的边或弧具有与它相关的数字，这种与图的边或弧相关的数叫做权。

在无向图G中，如果从顶点V到顶点V′有路径，则称V和V′是连通的。如果对于图中任意两个顶点Vi、Vj∈E，Vi和Vj都是连通的，则称G是连通图（Connected Graph）。

上面右图是连通图。

无向图顶点的边数叫度，有向图顶点的边数叫出度和入度。

左图中度为3（顶点E和顶点D的度都为3），右图中A的出度为1，入度为2。

二、图的存储结构

由于图的结构比较复杂，任意两个顶点之间都可能存在联系，因此无法以数据元素在内存中的物理位置来表示元素之间的关系。也就是说，图不可能用简单的顺序存储结构来表示。下面的四张图是同一张图。

2.1 邻接矩阵

考虑到图是由顶点和边或弧两部分组成，合在一起比较困难，那就很自然的考虑到分两个结构来分别存储。顶点部分大小、主次，所以用一个一位数组来存储是很不错的选择。而边或弧由于是顶点与顶点之间的关系，一维搞不懂，那就考虑用一个二维数组来存储。于是我们的邻接矩阵的方案就诞生了。

图的临界矩阵（Adjacency Matrix）存储方式是用两个数组来表示图。一个一维数组存储图中顶点信息，一个二维数组（称为临界矩阵）存储图中的边或弧的信息。

看一个实例，下面的左图是一个无向图，右边是这个无向图的邻接矩阵表示，其中1表示两个顶点之间有边，0表示顶点之间没有边：

再来看一个有向图，如下左图，右边的邻接矩阵，横向表示出度，纵向表示入度：

下面左图是一个带权的有向图，右边是它的邻接矩阵，其中的数字表示权，如果是∞表示没有弧，这叫带权邻接矩阵：

2.2 邻接表

邻接表，存储方法跟树的孩子链表示法相类似，是一种顺序分配和链式分配相结合的存储结构。如这个表头结点所对应的顶点存在相邻顶点，则把相邻顶点依次存放于表头结点所指向的单向链表中。

无向图的邻接表：

有向图的邻接表：

逆邻接表：

带权值的邻接表：

综上，图可以用邻接矩阵和邻接表表示。

三、图的遍历

图的遍历和树的遍历类似，我们希望从图中某一顶点出发访遍图中其余顶点，且使每一个顶点仅被访问一次，这一过程就叫做图的遍历。

13.1 深度优先遍历（Depth First Search， DFS）

从图中某个顶点V出发，访问此顶点，然后从V的未被访问的邻接点出发，深度优先遍历图，直到图中所有和V有路径相通的顶点都被访问到。

13.2 广度优先遍历（Broad First Search，BFS）

广度优先遍历算法是图的另一种基本遍历算法，其基本思想是尽最大程度辐射能够覆盖的节点，并对其进行访问。广度优先遍历就像在平静的湖面丢入一块石头，荡起的波

四、图的最小生成树

假设你是电信的实施工程师，需要为一个镇的九个村庄架设通信网络做设计，村庄位置大致如下图所示：

其中V0~V8是村庄，之间连线的数字表示村与村之间的可通达的直线距离。你们领导要求你必须用最小的成本完成这次任务，你说怎么办？有如下方案：

一个连通图的最小生成树是一个极小的连通字图，它包含图中全部的顶点，但只有足以构成一棵树的n-1条边。我们把构造连通网的最小代价生成树，称为最小生成树。

找连通网的最小生成树，经典的算法有两种：普里姆算法和克鲁斯卡尔算法。

普里姆算法的思想是从已选顶点所关联的未选边中找出权重最小的边，并且生成树不存在环。其中，已选顶点是构成最小生成树的结点，未选边是不属于生成树中的边。

对于下面这棵树，分析普里姆算法的实现步骤。

假设我们从顶点v1开始，所以我们可以发现（v1,v3）边的权重最小，所以第一个输出的边就是：v1—v3=1：

然后，我们要从v1和v3作为起点的边中寻找权重最小的边，首先了（v1,v3）已经访问过了，所以我们从其他边中寻找，发现(v3,v6)这条边最小，所以输出边就是：v3—v6=4：

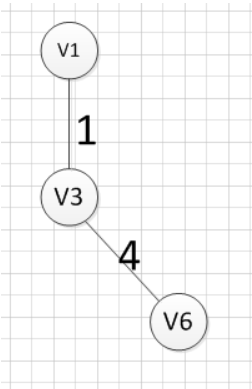
然后，我们要从v1、v3、v6这三个点相关联的边中寻找一条权重最小的边，我们可以发现边(v6,v4)权重最小，所以输出边就是：v6—v4=2：

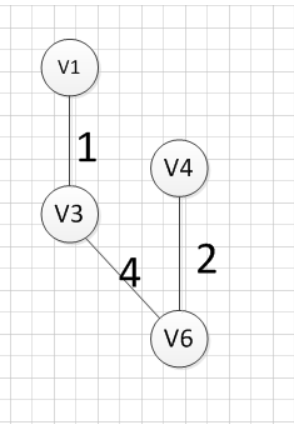
然后，我们就从v1、v3、v6、v4这四个顶点相关联的边中寻找权重最小的边，发现边（v3，v2）的权重最小，所以输出边v3—v2=5：

然后，我们就从v1、v3、v6、v4，v2这五个顶点相关联的边中寻找权重最小的边，发现边（v2，v5）的权重最小，所以输出边：v2—–v5=3：

最后，我们发现六个点都已经加入到集合U了，我们的最小生成树建立完成。

代码实现如下（代码包括深度优先遍历、广度优先遍历和普里姆算法）：

package com.wuychn.graph;

import java.util.LinkedList;

@SuppressWarnings("all")
public class Graph {

    private int vertexSize;// 顶点数量
    private int[] vertexs;// 顶点数组
    private int[][] matrix;
    private static final int MAX_WEIGHT = 1000;
    private boolean[] isVisited;

    public Graph(int vertexSize) {
        this.vertexSize = vertexSize;
        matrix = new int[vertexSize][vertexSize];
        vertexs = new int[vertexSize];
        for (int i = 0; i < vertexSize; i++) {
            vertexs[i] = i;
        }
        isVisited = new boolean[vertexSize];
    }

    /**
     * 获取某个顶点的出度
     *
     * @return
     */
    public int getOutDegree(int index) {
        int degree = 0;
        for (int j = 0; j < matrix[index].length; j++) {
            int weight = matrix[index][j];
            if (weight != 0 && weight != MAX_WEIGHT) {
                degree++;
            }
        }
        return degree;
    }

    /**
     * 获取某个顶点的入度
     *
     * @return
     */
    public int getInDegree(int index) {
        int degree = 0;
        for (int j = 0; j < matrix[index].length; j++) {
            int weight = matrix[j][index];
            if (weight != 0 && weight != MAX_WEIGHT) {
                degree++;
            }
        }
        return degree;
    }

    /**
     * 获取某个顶点的第一个邻接点
     */
    public int getFirstNeighbor(int index) {
        for (int j = 0; j < vertexSize; j++) {
            if (matrix[index][j] > 0 && matrix[index][j] < MAX_WEIGHT) {
                return j;
            }
        }
        return -1;
    }

    /**
     * 根据前一个邻接点的下标来取得下一个邻接点
     *
     * @param v1 表示要找的顶点
     * @param v2 表示该顶点相对于哪个邻接点去获取下一个邻接点
     */
    public int getNextNeighbor(int v, int index) {
        for (int j = index + 1; j < vertexSize; j++) {
            if (matrix[v][j] > 0 && matrix[v][j] < MAX_WEIGHT) {
                return j;
            }
        }
        return -1;
    }

    /**
     * 图的深度优先遍历算法
     */
    private void depthFirstSearch(int i) {
        isVisited[i] = true;
        int w = getFirstNeighbor(i);//
        while (w != -1) {
            if (!isVisited[w]) {
                // 需要遍历该顶点
                System.out.println("访问到了：" + w + "顶点");
                depthFirstSearch(w);
            }
            w = getNextNeighbor(i, w);//第一个相对于w的邻接点
        }
    }

    /**
     * 对外公开的深度优先遍历
     */
    public void depthFirstSearch() {
        isVisited = new boolean[vertexSize];
        for (int i = 0; i < vertexSize; i++) {
            if (!isVisited[i]) {
                System.out.println("访问到了：" + i + "顶点");
                depthFirstSearch(i);
            }
        }
        isVisited = new boolean[vertexSize];
    }

    /**
     * 图的广度优先遍历算法
     *
     * @param i
     */
    private void broadFirstSearch(int i) {
        int u, w;
        LinkedList<Integer> queue = new LinkedList<Integer>();
        System.out.println("访问到：" + i + "顶点");
        isVisited[i] = true;
        queue.add(i);//第一次把v0加到队列
        while (!queue.isEmpty()) {
            u = (Integer) (queue.removeFirst()).intValue();
            w = getFirstNeighbor(u);
            while (w != -1) {
                if (!isVisited[w]) {
                    System.out.println("访问到了：" + w + "顶点");
                    isVisited[w] = true;
                    queue.add(w);
                }
                w = getNextNeighbor(u, w);
            }
        }
    }

    /**
     * 对外公开的广度优先遍历
     */
    public void broadFirstSearch() {
        isVisited = new boolean[vertexSize];
        for (int i = 0; i < vertexSize; i++) {
            if (!isVisited[i]) {
                broadFirstSearch(i);
            }
        }
    }

    /**
     * prim 普里姆算法
     */
    public void prim() {
        int[] lowcost = new int[vertexSize];//最小代价顶点权值的数组,为0表示已经获取最小权值
        int[] adjvex = new int[vertexSize];//放顶点权值
        int min, minId, sum = 0;
        for (int i = 1; i < vertexSize; i++) {
            lowcost[i] = matrix[0][i];
        }
        for (int i = 1; i < vertexSize; i++) {
            min = MAX_WEIGHT;
            minId = 0;
            for (int j = 1; j < vertexSize; j++) {
                if (lowcost[j] < min && lowcost[j] > 0) {
                    min = lowcost[j];
                    minId = j;
                }
            }
            System.out.println("顶点：" + adjvex[minId] + "权值：" + min);
            sum += min;
            lowcost[minId] = 0;
            for (int j = 1; j < vertexSize; j++) {
                if (lowcost[j] != 0 && matrix[minId][j] < lowcost[j]) {
                    lowcost[j] = matrix[minId][j];
                    adjvex[j] = minId;
                }
            }
        }
        System.out.println("最小生成树权值和:" + sum);
    }

    /**
     * 获取两个顶点之间的权值
     *
     * @return
     */
    public int getWeight(int v1, int v2) {
        int weight = matrix[v1][v2];
        return weight == 0 ? 0 : (weight == MAX_WEIGHT ? -1 : weight);
    }

    public int getVertexSize() {
        return vertexSize;
    }

    public void setVertexSize(int vertexSize) {
        this.vertexSize = vertexSize;
    }

    public int[][] getMatrix() {
        return matrix;
    }

    public void setMatrix(int[][] matrix) {
        this.matrix = matrix;
    }

    public int[] getVertexs() {
        return vertexs;
    }

    public void setVertexs(int[] vertexs) {
        this.vertexs = vertexs;
    }

    public static void main(String[] args) {
        Graph graph = new Graph(9);

        int[] a1 = new int[]{0, 10, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, 11, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT};
        int[] a2 = new int[]{10, 0, 18, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, 16, MAX_WEIGHT, 12};
        int[] a3 = new int[]{MAX_WEIGHT, MAX_WEIGHT, 0, 22, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, 8};
        int[] a4 = new int[]{MAX_WEIGHT, MAX_WEIGHT, 22, 0, 20, MAX_WEIGHT, MAX_WEIGHT, 16, 21};
        int[] a5 = new int[]{MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, 20, 0, 26, MAX_WEIGHT, 7, MAX_WEIGHT};
        int[] a6 = new int[]{11, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, 26, 0, 17, MAX_WEIGHT, MAX_WEIGHT};
        int[] a7 = new int[]{MAX_WEIGHT, 16, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, 17, 0, 19, MAX_WEIGHT};
        int[] a8 = new int[]{MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, 16, 7, MAX_WEIGHT, 19, 0, MAX_WEIGHT};
        int[] a9 = new int[]{MAX_WEIGHT, 12, 8, 21, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, 0};

        graph.matrix[0] = a1;
        graph.matrix[1] = a2;
        graph.matrix[2] = a3;
        graph.matrix[3] = a4;
        graph.matrix[4] = a5;
        graph.matrix[5] = a6;
        graph.matrix[6] = a7;
        graph.matrix[7] = a8;
        graph.matrix[8] = a9;

        System.out.println("v2的出度:" + graph.getOutDegree(2));
        System.out.println("-----------------");
        System.out.println("v2的入度:" + graph.getInDegree(2));
        System.out.println("-----------------");
        System.out.println("权值：" + graph.getWeight(2, 3));
        System.out.println("-----------------");
        graph.depthFirstSearch();
        System.out.println("-----------------");
        graph.broadFirstSearch();
        System.out.println("-----------------");
        graph.prim();

    }
}

克鲁斯卡尔算法的思想是：

a. 将边按权值从小到大的顺序添加到新图中，保证添加的过程中不会形成环；

b. 重复上一步直到连接所有顶点，此时就生成了最小生成树。这是一种贪心策略。

将图中所有边按照权重大小从小到大一个一个按顺序组合成最小生成树，如果在组合过程新加入的边会导致生成树形成环，那这条边就舍弃，直到所有顶点都添加到生成树中为止。

这里同样我们给出一个和Prim算法讲解中同样的例子，模拟克鲁斯卡算法生成最小生成树的详细的过程。

完整的图如下：

我们需要从这些边中找出权重最小的那条边，可以发现边（v1，v3）这条边的权重是最小的，所以我们输出边：v1—v3=1：

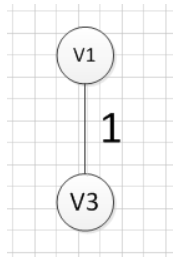
然后，我们需要在剩余的边中，再次寻找一条权重最小的边，可以发现边（v4，v6）这条边的权重最小，所以输出边：v4—v6=2：

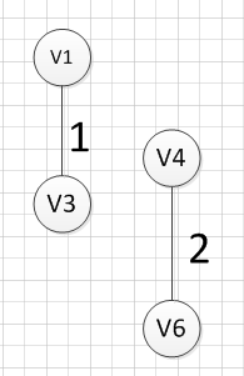
我们再次从剩余边中寻找权重最小的边，发现边（v2，v5）的权重最小，所以可以输出边：v2—v5=3：

我们使用同样的方式找出了权重最小的边：（v3，v6），所以我们输出边：v3—v6=4：

好了，现在我们还需要找出最后一条边就可以构造出一颗最小生成树，但是这个时候我们有三个选择：（v1,V4），（v2，v3），（v3，v4）,这三条边的权重都是5，首先我们如果选（v1，v4）的话，得到的图如下： 

这肯定是不符合我们算法要求的，因为它出现了一个环。同理，（v3，v4）这条边也是不行的。我们使用（v2，v3）试试，得到图形如下：

我们发现，这个图中没有环出现，而且把所有的顶点都加入到了这颗树上了，所以（v2，v3）就是我们所需要的边，所以最后一个输出的边就是：v2—v3=5。

克鲁斯卡尔算法的代码如下：

package com.wuychn.graph;

@SuppressWarnings("all")
public class GraphKruskal {

    private Edge[] edges;
    private int edgeSize;

    public GraphKruskal(int edgeSize) {
        this.edgeSize = edgeSize;
        edges = new Edge[edgeSize];
    }

    public void miniSpanTreeKruskal() {
        int m, n, sum = 0;
        int[] parent = new int[edgeSize];//神奇的数组，下标为起点，值为终点
        for (int i = 0; i < edgeSize; i++) {
            parent[i] = 0;
        }
        for (int i = 0; i < edgeSize; i++) {
            n = find(parent, edges[i].begin);
            m = find(parent, edges[i].end);
            if (n != m) {
                parent[n] = m;
                System.out.println("起始顶点：" + edges[i].begin + "---结束顶点：" + edges[i].end + "~权值：" + edges[i].weight);
                sum += edges[i].weight;
            } else {
                System.out.println("第" + i + "条边回环了");
            }
        }
        System.out.println("sum:" + sum);
    }


    /**
     * 将神奇数组进行查询获取非回环的值
     */
    public int find(int[] parent, int f) {
        while (parent[f] > 0) {
            System.out.println("找到起点" + f);
            f = parent[f];
            System.out.println("找到终点:" + f);
        }
        return f;
    }

    public void createEdgeArray() {
        Edge edge0 = new Edge(4, 7, 7);
        Edge edge1 = new Edge(2, 8, 8);
        Edge edge2 = new Edge(0, 1, 10);
        Edge edge3 = new Edge(0, 5, 11);
        Edge edge4 = new Edge(1, 8, 12);
        Edge edge5 = new Edge(3, 7, 16);
        Edge edge6 = new Edge(1, 6, 16);
        Edge edge7 = new Edge(5, 6, 17);
        Edge edge8 = new Edge(1, 2, 18);
        Edge edge9 = new Edge(6, 7, 19);
        Edge edge10 = new Edge(3, 4, 20);
        Edge edge11 = new Edge(3, 8, 21);
        Edge edge12 = new Edge(2, 3, 22);
        Edge edge13 = new Edge(3, 6, 24);
        Edge edge14 = new Edge(4, 5, 26);
        edges[0] = edge0;
        edges[1] = edge1;
        edges[2] = edge2;
        edges[3] = edge3;
        edges[4] = edge4;
        edges[5] = edge5;
        edges[6] = edge6;
        edges[7] = edge7;
        edges[8] = edge8;
        edges[9] = edge9;
        edges[10] = edge10;
        edges[11] = edge11;
        edges[12] = edge12;
        edges[13] = edge13;
        edges[14] = edge14;
    }

    class Edge {
        private int begin;
        private int end;
        private int weight;

        public Edge(int begin, int end, int weight) {
            super();
            this.begin = begin;
            this.end = end;
            this.weight = weight;
        }

        public int getBegin() {
            return begin;
        }

        public void setBegin(int begin) {
            this.begin = begin;
        }

        public int getEnd() {
            return end;
        }

        public void setEnd(int end) {
            this.end = end;
        }

        public int getWeight() {
            return weight;
        }

        public void setWeight(int weight) {
            this.weight = weight;
        }

    }

    public static void main(String[] args) {
        GraphKruskal graphKruskal = new GraphKruskal(15);
        graphKruskal.createEdgeArray();
        graphKruskal.miniSpanTreeKruskal();
    }
}

本节中普里姆算法和克鲁斯卡尔算法的推理过程来自https://blog.csdn.net/qq_36951116/article/details/83089039。

五、最短路径

图的最短路径是指从有向图中某一顶点（起始顶点）到达另一顶点（终止顶点）的路径中，其权值之和最小的路径。

 

迪杰斯特拉(Dijkstra)算法是典型最短路径算法，用于计算一个顶点到其他顶点的最短路径。它的主要特点是以起始点为中心向外层层扩展（广度优先搜索思想），直到扩展到终点为止。

基本思想

通过Dijkstra计算图G中的最短路径时，需要指定起点s(即从顶点s开始计算)。

此外，引进两个集合S和U。S的作用是记录已求出最短路径的顶点(以及相应的最短路径长度)，而U则是记录还未求出最短路径的顶点(以及该顶点到起点s的距离)。

初始时，S中只有起点s；U中是除s之外的顶点，并且U中顶点的路径是”起点s到该顶点的路径”。然后，从U中找出路径最短的顶点，并将其加入到S中；接着，更新U中的顶点和顶点对应的路径。 然后，再从U中找出路径最短的顶点，并将其加入到S中；接着，更新U中的顶点和顶点对应的路径 ...… 重复该操作，直到遍历完所有顶点。

图解

以上图G4为例，来对迪杰斯特拉进行算法演示(以第4个顶点D为起点)。

初始状态：S是已计算出最短路径的顶点集合，U是未计算除最短路径的顶点的集合。

第1步：将顶点D加入到S中。 此时，S={D(0)}, U={A(∞),B(∞),C(3),E(4),F(∞),G(∞)}。 注:C(3)表示C到起点D的距离是3。

第2步：将顶点C加入到S中。 上一步操作之后，U中顶点C到起点D的距离最短；因此，将C加入到S中，同时更新U中顶点的距离。以顶点F为例，之前F到D的距离为∞；但是将C加入到S之后，F到D的距离为9=(F,C)+(C,D)。 此时，S={D(0),C(3)}, U={A(∞),B(23),E(4),F(9),G(∞)}。

第3步：将顶点E加入到S中。 上一步操作之后，U中顶点E到起点D的距离最短；因此，将E加入到S中，同时更新U中顶点的距离。还是以顶点F为例，之前F到D的距离为9；但是将E加入到S之后，F到D的距离为6=(F,E)+(E,D)。 此时，S={D(0),C(3),E(4)}, U={A(∞),B(23),F(6),G(12)}。

第4步：将顶点F加入到S中。 此时，S={D(0),C(3),E(4),F(6)}, U={A(22),B(13),G(12)}。

第5步：将顶点G加入到S中。 此时，S={D(0),C(3),E(4),F(6),G(12)}, U={A(22),B(13)}。

第6步：将顶点B加入到S中。 此时，S={D(0),C(3),E(4),F(6),G(12),B(13)}, U={A(22)}。

第7步：将顶点A加入到S中。 此时，S={D(0),C(3),E(4),F(6),G(12),B(13),A(22)}。

此时，起点D到各个顶点的最短距离就计算出来了：A(22) B(13) C(3) D(0) E(4) F(6) G(12)。

本节以上内容来自：https://blog.csdn.net/heroacool/article/details/51014824

代码

package com.wuychn.data_structures.graph;

/**
 * 求图的最短路径：迪杰斯特拉算法
 */
@SuppressWarnings("all")
public class DnjavaDijstra {

    private final static int MAXVEX = 9;
    private final static int MAXWEIGHT = 65535;
    private int shortTablePath[] = new int[MAXVEX];// 记录的是v0到某顶点的最短路径和

    /**
     * 获取一个图的最短路径
     */
    public void shortestPathDijstra(Graph graph) {
        int min;
        int k = 0;// 记录下标
        boolean isgetPath[] = new boolean[MAXVEX];
        for (int v = 0; v < graph.getVertexSize(); v++) {
            shortTablePath[v] = graph.getMatrix()[0][v];// 获取v0这一行的权值数组
        }
        shortTablePath[0] = 0;
        isgetPath[0] = true;
        for (int v = 1; v < graph.getVertexSize(); v++) {
            min = MAXWEIGHT;
            for (int w = 0; w < graph.getVertexSize(); w++) {
                if (!isgetPath[w] && shortTablePath[w] < min) {
                    k = w;
                    min = shortTablePath[w];
                }
            }
            isgetPath[k] = true;
            for (int j = 0; j < graph.getVertexSize(); j++) {
                if (!isgetPath[j] && (min + graph.getMatrix()[k][j] < shortTablePath[j])) {
                    shortTablePath[j] = min + graph.getMatrix()[k][j];
                }
            }
        }
        for (int i = 0; i < shortTablePath.length; i++) {
            System.out.println("V0到V" + i + "的最短路径为:" + shortTablePath[i] + "\n");
        }

    }

    public static void main(String[] args) {
        Graph graph = new Graph(MAXVEX);
        graph.createGraph();
        DnjavaDijstra dijstra = new DnjavaDijstra();
        dijstra.shortestPathDijstra(graph);
    }
}

十六、拓扑排序

对于一部电影的制作过程，我们可以看成是一个项目工程。所有的工程都可以分为若干个"活动"的自工程。在这些活动之间，通常会受到一定的条件约束，如其中某些活动必须在另一些活动完成之后才能开始。比如，电影制作不可能在人员到位进驻场地时，导演还没有找到，也不可能在拍摄过程中，场地都没有。这些听起来就很荒谬。

在一个表示工程的有向图中，用顶点表示活动，用弧表示活动之间的优先关系，这样的有向图为顶点表示活动的网，我们成为AOV网（Activity On Vertex Network）。AOV网中的弧表示活动之间存在的某种制约关系。

设G=(V, E)是一个具有n个顶点的有向图，V中的顶点序列V1,V2,....Vn满足若从顶点Vi到Vj有一条路径，则在顶点序列中顶点Vi必须在顶点Vj之前。则我们称这样的顶点序列为一个拓扑序列。

那么拓扑排序，其实就是对一个有向图构造拓扑序列的过程。构造时有两个结果：

1、如果此网的全部顶点都被输出，说明该网是不存在环的AOV网

2、如果输出的顶点数少了，说明这个网存在环，不是一个AOV网

算法思路：从AOV网中选择一个入度为0的顶点输出，然后删去此顶点，并删除以此顶点为尾的弧。继续重复此步骤，直到输出全部顶点或者AOV网中不存在入度为0的顶点为止。

算法实现：

package com.wuychn.data_structures.graph;

import java.util.Stack;

/**
 * 有向图的拓扑排序
 */
@SuppressWarnings("all")
public class DnGraphTopologic {
    private int numVertexes;
    private VertexNode[] adjList;//邻接顶点的一维数组

    public DnGraphTopologic(int numVertexes) {
        this.numVertexes = numVertexes;
    }

    private void createGraph() {
        VertexNode node0 = new VertexNode(0, "v0");
        VertexNode node1 = new VertexNode(0, "v1");
        VertexNode node2 = new VertexNode(2, "v2");
        VertexNode node3 = new VertexNode(0, "v3");
        VertexNode node4 = new VertexNode(2, "v4");
        VertexNode node5 = new VertexNode(3, "v5");
        VertexNode node6 = new VertexNode(1, "v6");
        VertexNode node7 = new VertexNode(2, "v7");
        VertexNode node8 = new VertexNode(2, "v8");
        VertexNode node9 = new VertexNode(1, "v9");
        VertexNode node10 = new VertexNode(1, "v10");
        VertexNode node11 = new VertexNode(2, "v11");
        VertexNode node12 = new VertexNode(1, "v12");
        VertexNode node13 = new VertexNode(2, "v13");
        adjList = new VertexNode[numVertexes];
        adjList[0] = node0;
        adjList[1] = node1;
        adjList[2] = node2;
        adjList[3] = node3;
        adjList[4] = node4;
        adjList[5] = node5;
        adjList[6] = node6;
        adjList[7] = node7;
        adjList[8] = node8;
        adjList[9] = node9;
        adjList[10] = node10;
        adjList[11] = node11;
        adjList[12] = node12;
        adjList[13] = node13;
        node0.firstEdge = new EdgeNode(11);
        node0.firstEdge.next = new EdgeNode(5);
        node0.firstEdge.next.next = new EdgeNode(4);
        node1.firstEdge = new EdgeNode(8);
        node1.firstEdge.next = new EdgeNode(4);
        node1.firstEdge.next.next = new EdgeNode(2);
        node2.firstEdge = new EdgeNode(9);
        node2.firstEdge.next = new EdgeNode(6);
        node2.firstEdge.next.next = new EdgeNode(5);
        node3.firstEdge = new EdgeNode(13);
        node3.firstEdge.next = new EdgeNode(2);
        node4.firstEdge = new EdgeNode(7);
        node5.firstEdge = new EdgeNode(12);
        node5.firstEdge.next = new EdgeNode(8);
        node6.firstEdge = new EdgeNode(5);
        node8.firstEdge = new EdgeNode(7);
        node9.firstEdge = new EdgeNode(11);
        node9.firstEdge.next = new EdgeNode(10);
        node10.firstEdge = new EdgeNode(13);
        node12.firstEdge = new EdgeNode(9);
    }

    /**
     * 拓扑排序
     *
     * @throws Exception
     * @author Administrator
     */
    private void topologicalSort() throws Exception {
        Stack<Integer> stack = new Stack<>();
        int count = 0;
        int k = 0;
        for (int i = 0; i < numVertexes; i++) {
            if (adjList[i].in == 0) {
                stack.push(i);
            }
        }
        while (!stack.isEmpty()) {
            int pop = stack.pop();
            System.out.println("顶点：" + adjList[pop].data);
            count++;
            for (EdgeNode node = adjList[pop].firstEdge; node != null; node = node.next) {
                k = node.adjVert;//下标
                if (--adjList[k].in == 0) {
                    stack.push(k);//入度为0,入栈
                }
            }
        }
        if (count < numVertexes) {
            throw new Exception("完犊子了，拓扑排序失败");
        }
    }

    //边表顶点
    class EdgeNode {
        private int adjVert;
        private EdgeNode next;
        private int weight;

        public EdgeNode(int adjVert) {
            this.adjVert = adjVert;
        }

        public int getAdjVert() {
            return adjVert;
        }

        public void setAdjVert(int adjVert) {
            this.adjVert = adjVert;
        }

        public EdgeNode getNext() {
            return next;
        }

        public void setNext(EdgeNode next) {
            this.next = next;
        }

        public int getWeight() {
            return weight;
        }

        public void setWeight(int weight) {
            this.weight = weight;
        }

    }

    //邻接顶点
    class VertexNode {
        private int in;//入度
        private String data;
        private EdgeNode firstEdge;

        public VertexNode(int in, String data) {
            this.in = in;
            this.data = data;
        }

        public int getIn() {
            return in;
        }

        public void setIn(int in) {
            this.in = in;
        }

        public String getData() {
            return data;
        }

        public void setData(String data) {
            this.data = data;
        }

        public EdgeNode getFirstEdge() {
            return firstEdge;
        }

        public void setFirstEdge(EdgeNode firstEdge) {
            this.firstEdge = firstEdge;
        }

    }

    public static void main(String[] args) {
        DnGraphTopologic dnGraphTopologic = new DnGraphTopologic(14);
        dnGraphTopologic.createGraph();
        try {
            dnGraphTopologic.topologicalSort();
        } catch (Exception e) {
            // TODO Auto-generated catch block
            e.printStackTrace();
        }
    }
}