数据结构-树

一边学习一边哭

已于 2022-11-15 00:03:29 修改

阅读量1.3k

点赞数

分类专栏：数据结构与算法文章标签：数据结构算法

于 2022-10-11 10:11:03 首次发布

本文链接：https://blog.csdn.net/qq522044637/article/details/126097728

版权

数据结构与算法专栏收录该内容

10 篇文章 2 订阅

订阅专栏

斜二叉树（Skewed Binary Tree）

完美二叉树/满二叉树（Perfect Binary Tree/Full Binary Tree）

完全二叉树（Complete Binary Tree）

二叉搜索树（BST, Binary Search Tree）

二叉搜索树的定义

二叉搜索树操作

判断是否同一颗二叉搜索树

平衡二叉树（Balance Binary Tree）

树的定义

树（Tree）：n（n>=0）结点构成的有限集合。

当n-0时，称为空树；

对于任一棵非空树（n>0），它具备以下性质:

树中有一个称为“根（Root）”的特殊节点，用r表示；
其余结点可分为m（m>0）个互不相交的有限集，其中每个集合本身又是一棵树，称为原来树的“子树（SubTree）”。

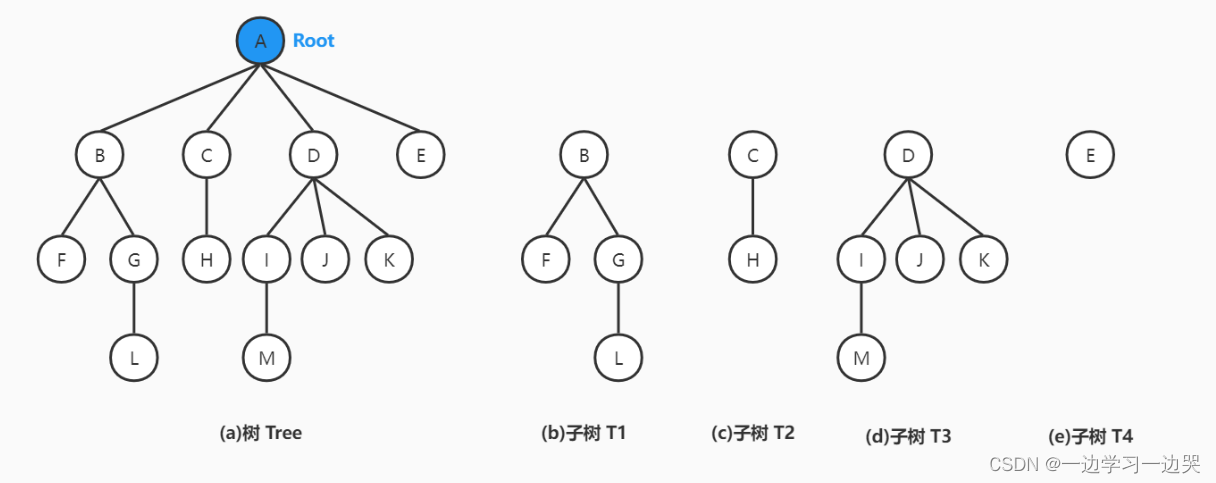
结论：

子树是不相交的；
除了根节点以外，每个节点有且仅有一个父节点；
一棵N个节点的树，有N-1条边（因为每个节点到父节点都有一条线，除了根节点）；
树是保证所有节点联通的一种最小的连接方式。

树有关的一些术语

结点的度（Degree）：结点的子树个数
树的度：树的所有结点中最大的度数
叶结点（Leaf）：度为0的结点
父结点（Parent）：有子树的结点，是其子树的根节点的父节点
子节点（Child）：若A结点是B结点的父结点，则称B结点是A结点的子结点；子结点也称孩子结点
兄弟结点（Sibling）：具有同一个父结点的各结点彼此是兄弟结点
路径和路径长度：从结点n1到结点nk的路径为一个结点序列。路径上所包含的边的个数就是路径长度。
祖先节点（Ancestor）：沿树根到某一结点的路径上的所有结点，都是这个结点的祖先结点。
子孙节点（Descesddant）：某一结点的子树中的所有结点，都是这个结点的子孙结点。
结点的层次（Level）：根结点在1层，其它任一结点的层数是其父结点的层数+1。
树的深度（Depth）：树中所有结点中的最大层次就是树的深度。

树的表示

树是否可以用数组来实现？

任何节点都有可能有一个或多个儿子，而使用数组这样的顺序存储来实现的话，不好表示结点之间的关系，只能表示顺序。

所以树比较适合用链表来实现。每个结点用一个结构来表示，结构中通过多个指针域指向多个儿子结点，能方便地实现树的结构。但是如果单纯考虑用多个指针域指向结点的多个子结点，由于有些结点有多个子结点，而有的结点甚至没有子结点，这样会带来空间上的浪费。

儿子-兄弟表示法

结构的一个指针指向子结点，另一个指针指向兄弟结点。

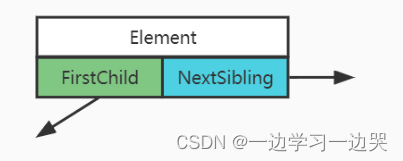
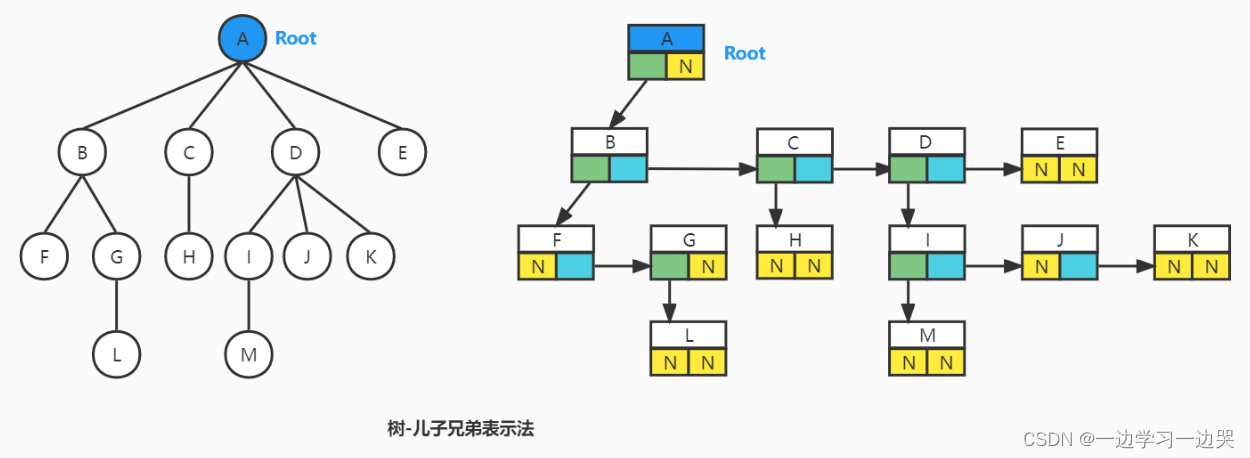
二叉树

二叉树的表示方法和儿子-兄弟表示法相似。一指针指向左子结点，一个指针指向右子结点。

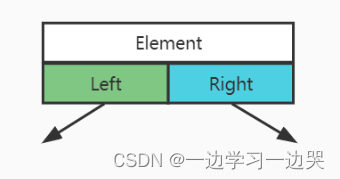
二叉树

二叉树的定义

二叉树：一个有穷的结点集合。

这个集合可以为空；
若不为空，它是由根结点和称为其左子树和右子树的两个不相交的二叉树组成；
二叉树的子树是有左右之分的，其他度为2的树子树是不分左右的；
二叉树的物种形态：（1）空树；（2）只有一个根结点；（3）有一个根结点，右左子树；（4）有一个根节点，有右子树；（5）有一个根节点，有左子树和右子树。

特殊的二叉树

斜二叉树（Skewed Binary Tree）

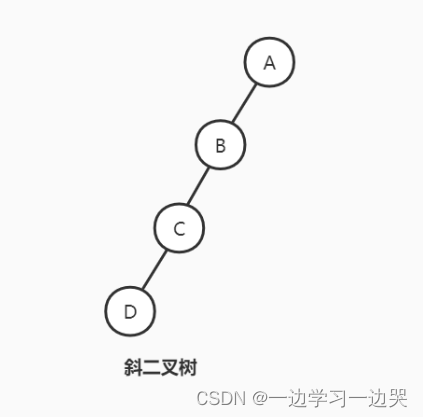
完美二叉树/满二叉树（Perfect Binary Tree/Full Binary Tree）

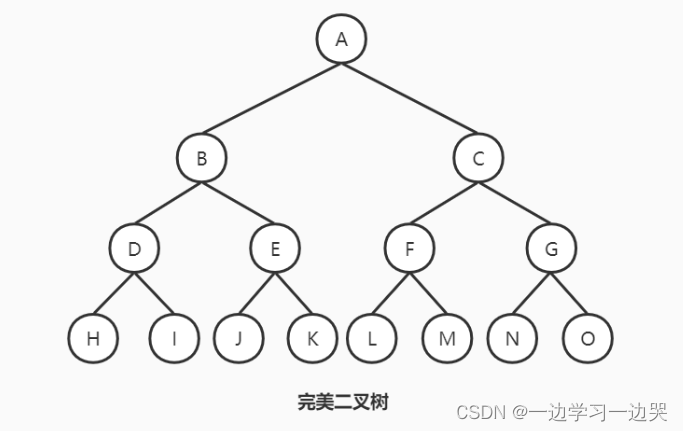
完全二叉树（Complete Binary Tree）

如果将完美二叉树的所有结点，按从上至下、从左至右的顺序进行编号。完全二叉树是允许缺失最后几个结点。换句话说，缺失完结点后，完全二叉树和完美二叉树的相同位置结点的编号也是相同的。

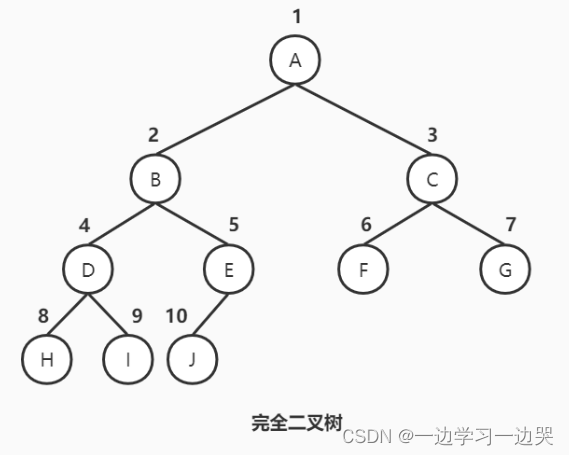
二叉树的重要性质

1.一个二叉树的第i层的最大节点数是： $2^{i-1}$ , i > 0

2.深度为K的二叉树的最大总结点数是： $2^{k}$ -1 , k > 0

3.对任何非空二叉树T，若 $n_{0}$ 表示叶结点、 $n_{1}$ 表示度为1的非叶结点个数、 $n_{2}$ 表示度为2的非叶结点个数，那么满足 $n_{0}=n_{2}+1$

证明：

   总边数 = 总结点数-1 = $n_{0}+n_{1}+n_{2}-1$

总边数 = 各结点向下的边 = $0 * n_{0} + 1 * n_{1} + 2 * n_{2}$ = $n_{1}+2n_{2}$

         $n_{0}+n_{1}+n_{2}-1=n_{1}+2n_{2}$

         $n_{0}=n_{2}+1$

二叉树的抽象数据类型

数据对象集：一个又穷的结点集合。若不为空，由根节点和其左、右二叉子树组成。

操作集：

创建一个二叉树
判断树是否为空
遍历二叉树，按某种顺序访问每个结点

常用遍历方法：

先序遍历 PreOrderTraversal：先序——根、左子树、右子树
中序遍历 InOrderTraversal：中序——左子树、根、右子树
后序遍历 PostOrderTraversal：后序——左子树、右子树、根
层次遍历 LevelOrderTraversal：层次——从上到下、从左到右

二叉树的存储结构

1.二叉树的顺序存储结构

使用数组存储二叉树，比较适合完美二叉树和完全二叉树。按从上至下、从左至右顺序存储。

一般的二叉树也可以使用数组存储，将一般二叉树补充成完全二叉树，将缺失的结点在数组中留下空位。但是会造成空间上的浪费。

n个结点的完全二叉树的父子关系：

非根结点（结点序号i>1），结点的父结点序号： $\frac{i}{2}$ , 取整
结点（结点序号为i），结点的左孩子序号：2i , （2i <= n）
结点（结点序号为i），结点的右孩子序号：2i+1 , （2i+1 <= n）

2.二叉树的链式存储结构

二叉树的表示方法和儿子-兄弟表示法相似。一指针指向左子结点，一个指针指向右子结点。

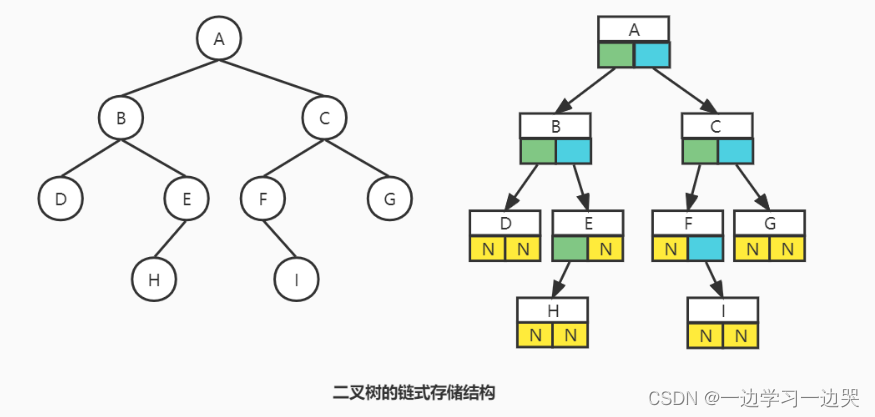
二叉树的应用

二叉搜索树（BST, Binary Search Tree）

二叉搜索树的定义

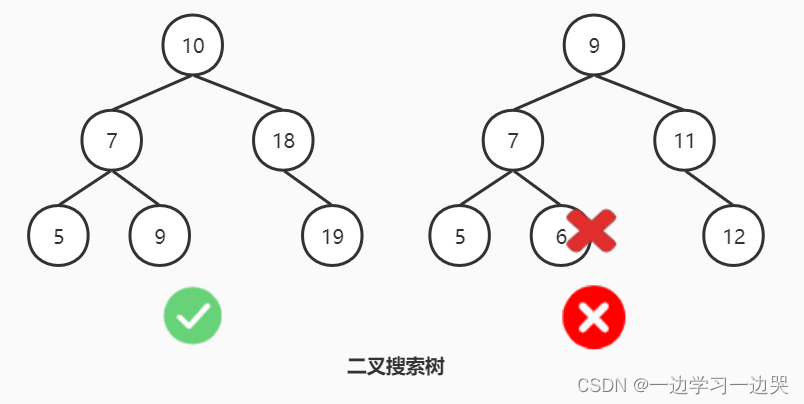
二叉搜索树，也称二叉排序树或二叉查找树。树上的任何一个节点的值，比所有的左子树的值都要大，比所有的右子树的值都要小。

二叉搜索树：可以为空；如果不空的时候，满足以下性质：

非空左子树的所有键值，都小于其根节点键值；
非空右子树的所有键值，都大于其根节点键值；
左、右子树都是二叉搜索树。

二叉搜索树操作

查找：

从二叉搜索树BST中查找元素X，返回其所在结点的地址；
从二叉搜索树BST中返回最小元素所在结点的地址；
从二叉搜索树BST中返回最大元素所在结点的地址。

查找元素X，只需要对比根节点。如果树为空，则返回NULL。如果树不为空，则将根节点和元素X比较：X小于根节点则到左子树继续查找；X大于根节点则到右子树继续查找；X等于根节点则查找完成。
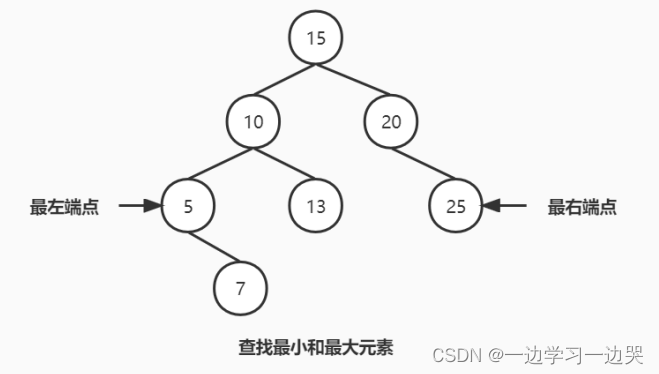
最大元素一定是在树的最右分枝的端结点上。
最小元素一定是在树的最左分枝的端结点上。

插入：在二叉搜索树BST上，插入新的值为X的结点。

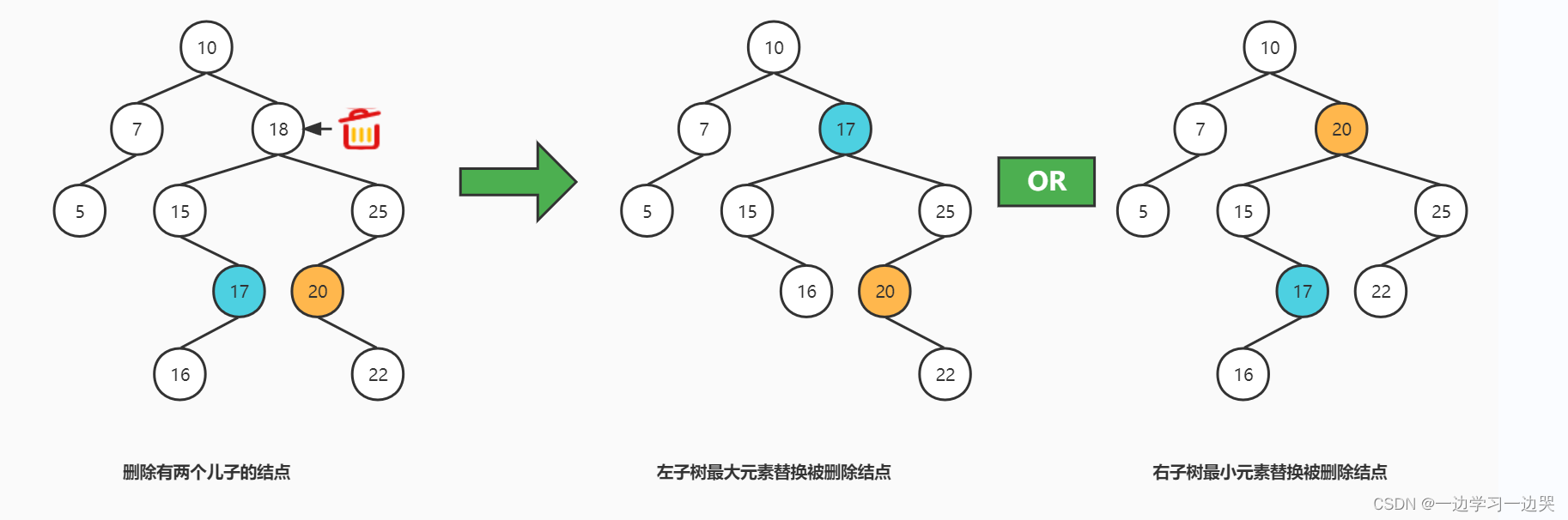
删除：在二叉搜索树BST上，删除值位X的结点。删除有三种情况：

删除的结点没有儿子，则父结点指向nil；
删除的结点有一个儿子，则父结点指向要删除的结点的儿子结点；
删除的结点有两个儿子，则使用左子树的最右边结点或右子树的最左边节点替换被删除的结点。因为这两个结点一定最多只有一个儿子。

判断是否同一颗二叉搜索树

补

平衡二叉树（Balance Binary Tree）

不同的结点插入顺序，会导致生成不一样的树。则树的深度和平均查找长度ASL也会不同。

ASL = (同一层结点数量 * 结点的层次) / 结点总数

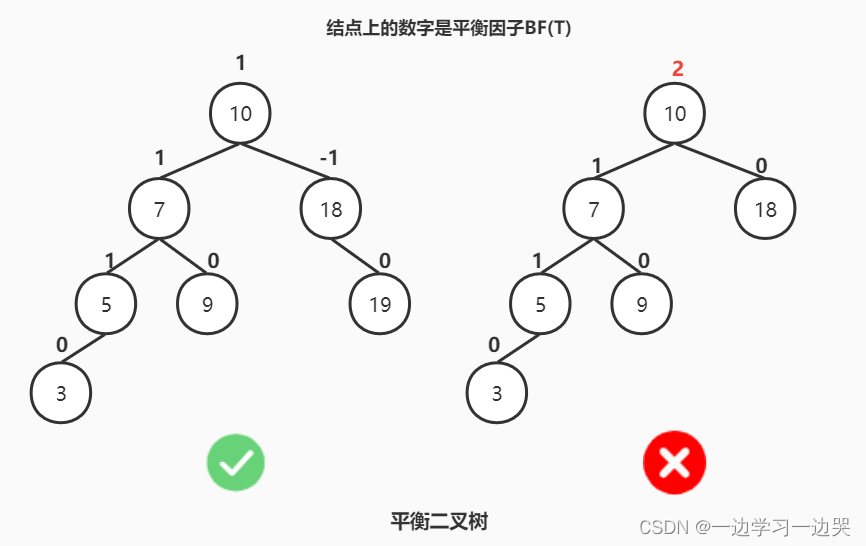
平衡因子（Balance Factor，简称BUF）：BF(T) = $h_{L}$ - $h_{R}$ ，其中 $h_{L}$ 、 $h_{R}$ 分别为T树的左子树和右子树的高度。

平衡二叉树的定义

平衡二叉树（Balance Binary Tree），又称AVL树（AVL是提出这个树的科学家名字缩写）。

平衡二叉树可以是一颗空树。如果不空的话，其任一结点左、右子树高度差的绝对值不超过1，即 $\left | BF(T) \right |\leqslant 1$

构成平衡二叉树的最少结点数

高度：平衡二叉树，1层高度为0，2层高度为1，以此类推。

构成平衡二叉树所需的最少结点数： $n_{h}=n_{h-1}+n_{h-2}+1$ 。 $n_{h}$ 表示高度为h的平衡二叉树的最少结点数，等于前两层最少节点数之和再加1。

高度为0，最少节点数为1；高度为1最少节点数为2。后续的最少结点数可以用公式算出来。

平衡二叉树的调整

一个结点，其子树被插入新的结点。则这个结点称为：“发现者”/“被破坏节点”；

插入的结点被称为：“麻烦节点”/“破坏节点”。

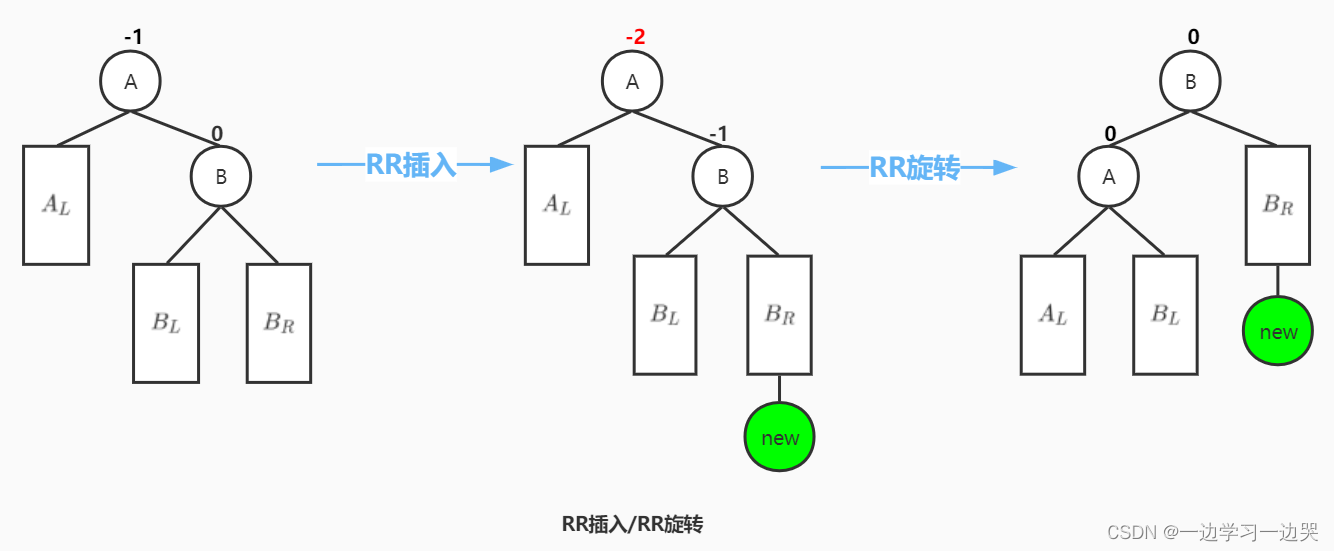
1.RR插入/RR旋转

插入的“破坏节点”，在“被破坏节点”的右子树的右子树上，因而叫RR插入。需要RR旋转（右单旋）。

RR旋转：被破坏结点为A，被破坏结点的左子树记为 $A_{L}$ ，被破坏结点的右子树的根节点为B，B的左、右子树记为 $B_{L}$ 、 $B_{R}$ 。将B结点提升为新的根节点，A作为B结点的左儿子， $A_{L}$ 还作为A结点的左子树； $B_{R}$ 还作为B结点的右子树； $B_{L}$ 变为A结点的右子树。

2.LL插入/LL旋转

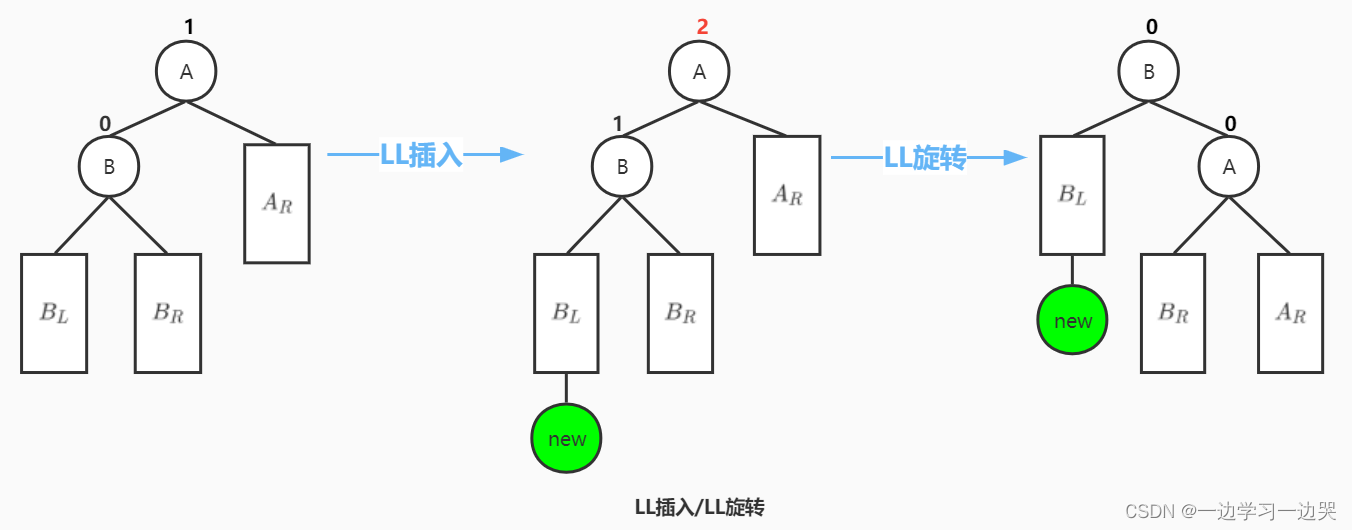
插入的“破坏节点”，在“被破坏节点”的左子树的左子树上，因而叫LL插入。需要LL旋转（左单旋）。

LL旋转：被破坏结点为A，被破坏结点的右子树记为 $A_{R}$ ，被破坏结点的左子树的根节点为B，B的左、右子树记为 $B_{L}$ 、 $B_{R}$ 。将B结点提升为新的根节点，A作为B结点的右儿子， $A_{R}$ 还作为A结点的右子树； $B_{L}$ 还作为B结点的左子树； $B_{R}$ 变为A结点的左子树。

3.LR插入/LR旋转

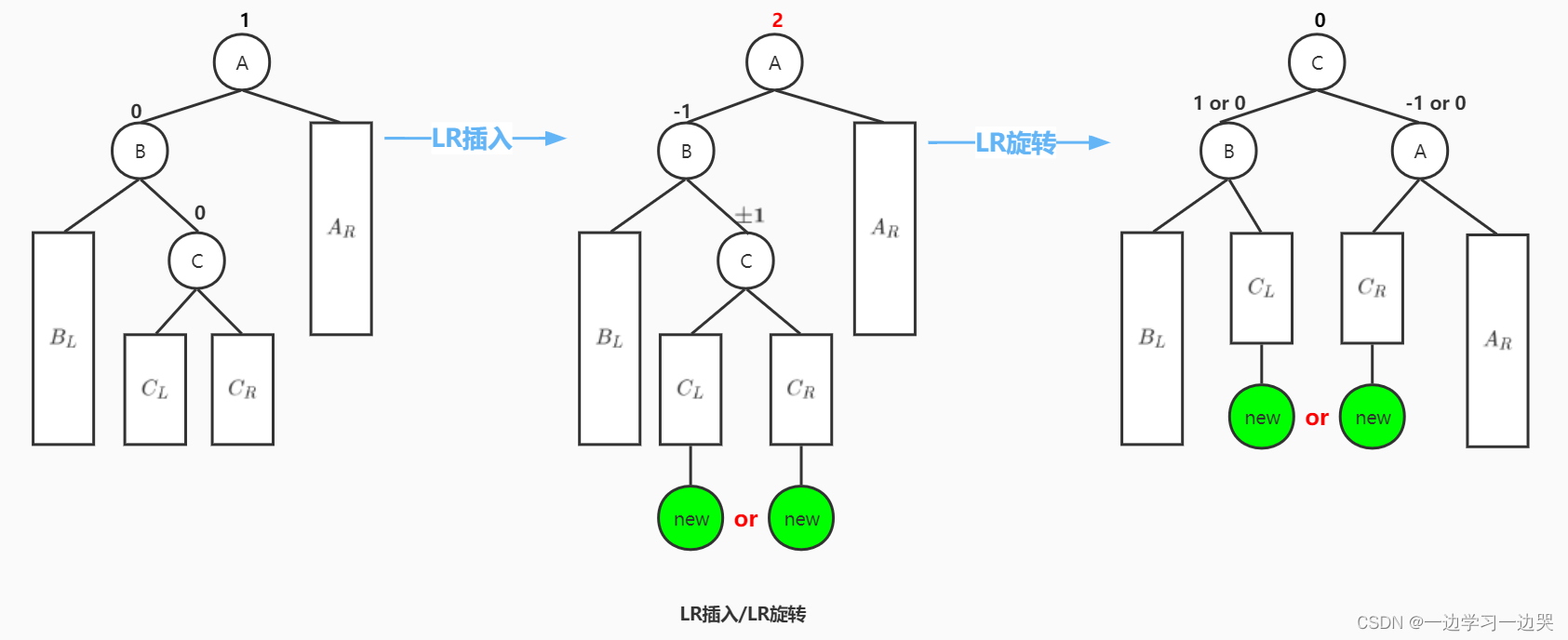
插入的“破坏节点”，在“被破坏节点”的左子树的右子树上，因而叫LR插入。需要LR旋转。

LR旋转：被破坏节点为A，A的左子树的根节点为B，A的右子树为 $A_{R}$ ；B的左子树为 $B_{L}$ ，B的右子树的根节点为C；C的左、右子树记为 $C_{L}$ 、 $C_{R}$ 。将C结点提升为新的根节点，B作为C结点的左儿子，A作为C的右儿子； $B_{L}$ 还作为B的左子树， $C_{L}$ 作为B的右子树； $C_{R}$ 作为A的左子树， $A_{R}$ 还作为A的右子树。

4.RL插入/RL旋转

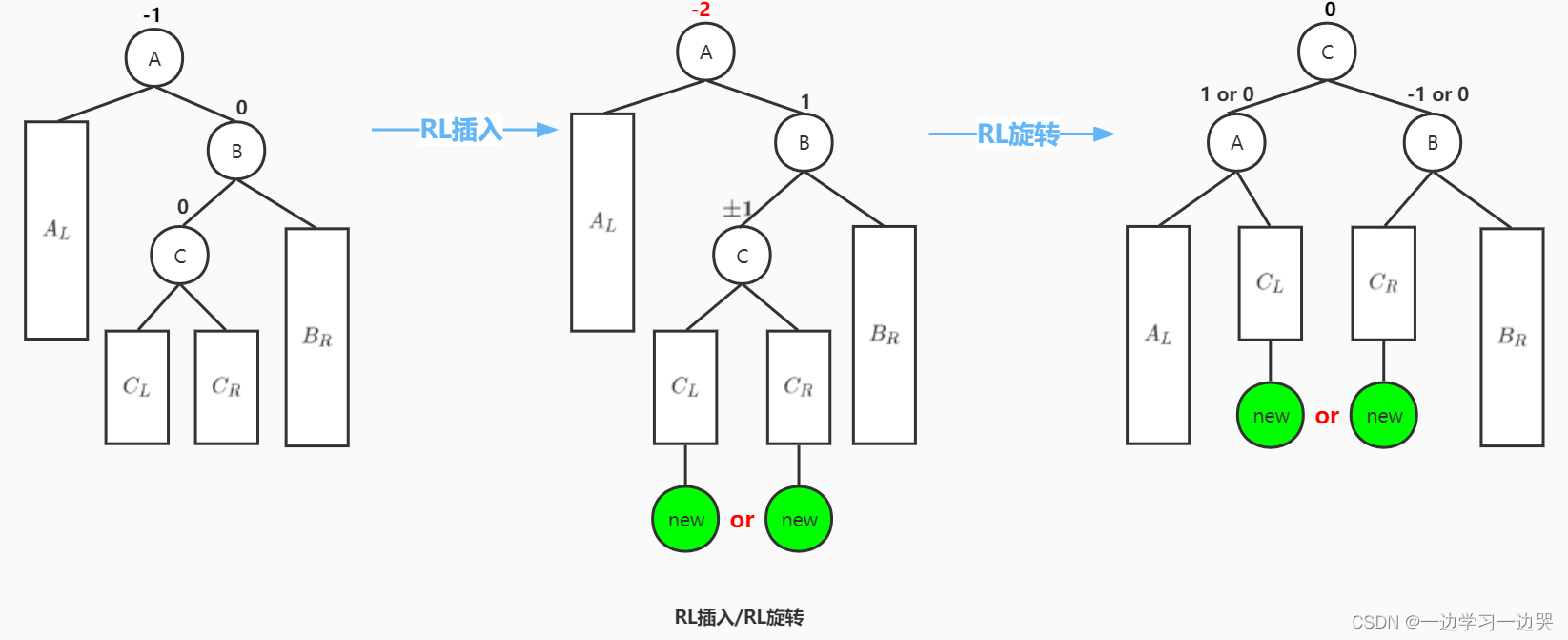
插入的“破坏节点”，在“被破坏节点”的右子树的左子树上，因而叫RL插入。需要RL旋转。

RL旋转：被破坏节点为A，A的左子树为 $A_{L}$ ，A的右子树为的根节点为B；B的左子树的根节点为C，B的右子树为 $B_{R}$ ；C的左、右子树记为 $C_{L}$ 、 $C_{R}$ 。将C结点提升为新的根节点，A作为C结点的左儿子，B作为C的右儿子； $A_{L}$ 还作为A的左子树， $C_{L}$ 作为A的右子树； $C_{R}$ 作为B的左子树， $B_{R}$ 还作为B的右子树。

哈夫曼树（Huffman Tree）

哈夫曼树的定义

带权路径长度(WPL)：设二叉树有n个叶子结点，每个叶子结点带有权值 $w_{k}$ ，从根结点到每个叶子结点的长度为 $l_{k}$ ，则每个叶子结点的带权路径长度之和就是： $WPL=\sum_{k=1}^{n}w_{k}\cdot l_{k}$

例：有五个叶子结点，它们的权值为{1,2,3,4,5}，用此权值序列可以构造出形状不同的多个二叉树。

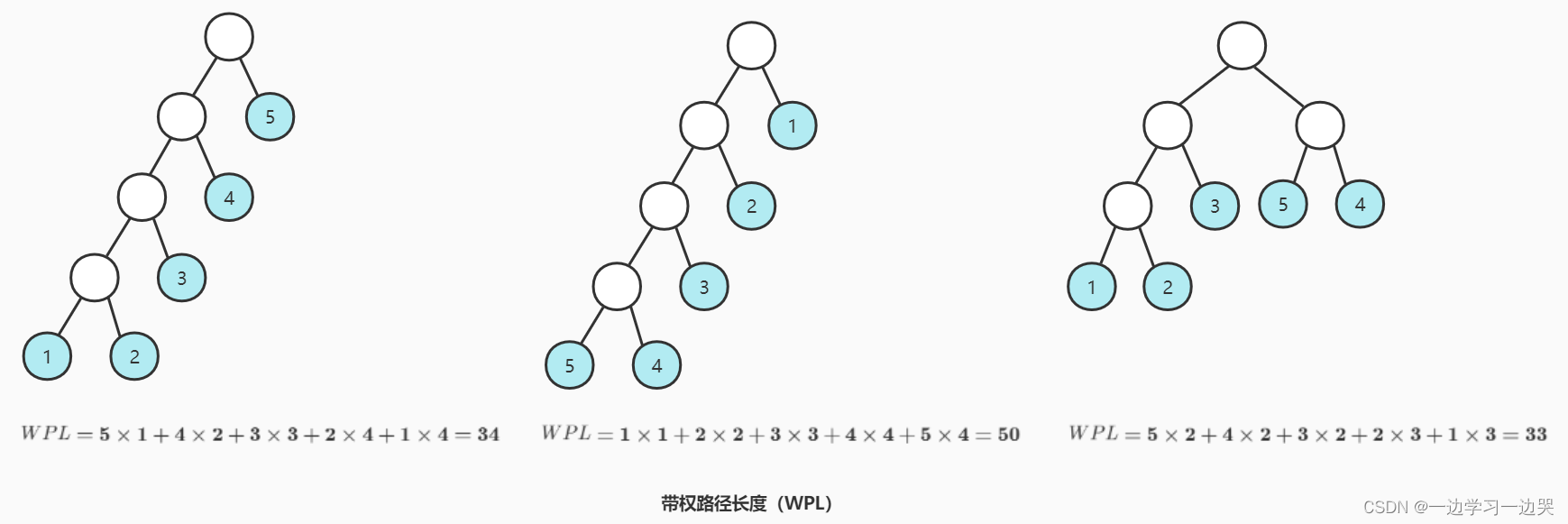
哈夫曼树（最优二叉树）：就是将二叉树的WPL降到最低（WPL最小的二叉树）。

哈夫曼树的构造

哈夫曼树的构造：每次把权值最小的两棵二叉树合并。合并得到一个新的结点，其权值是合并的两个结点的权值之和。

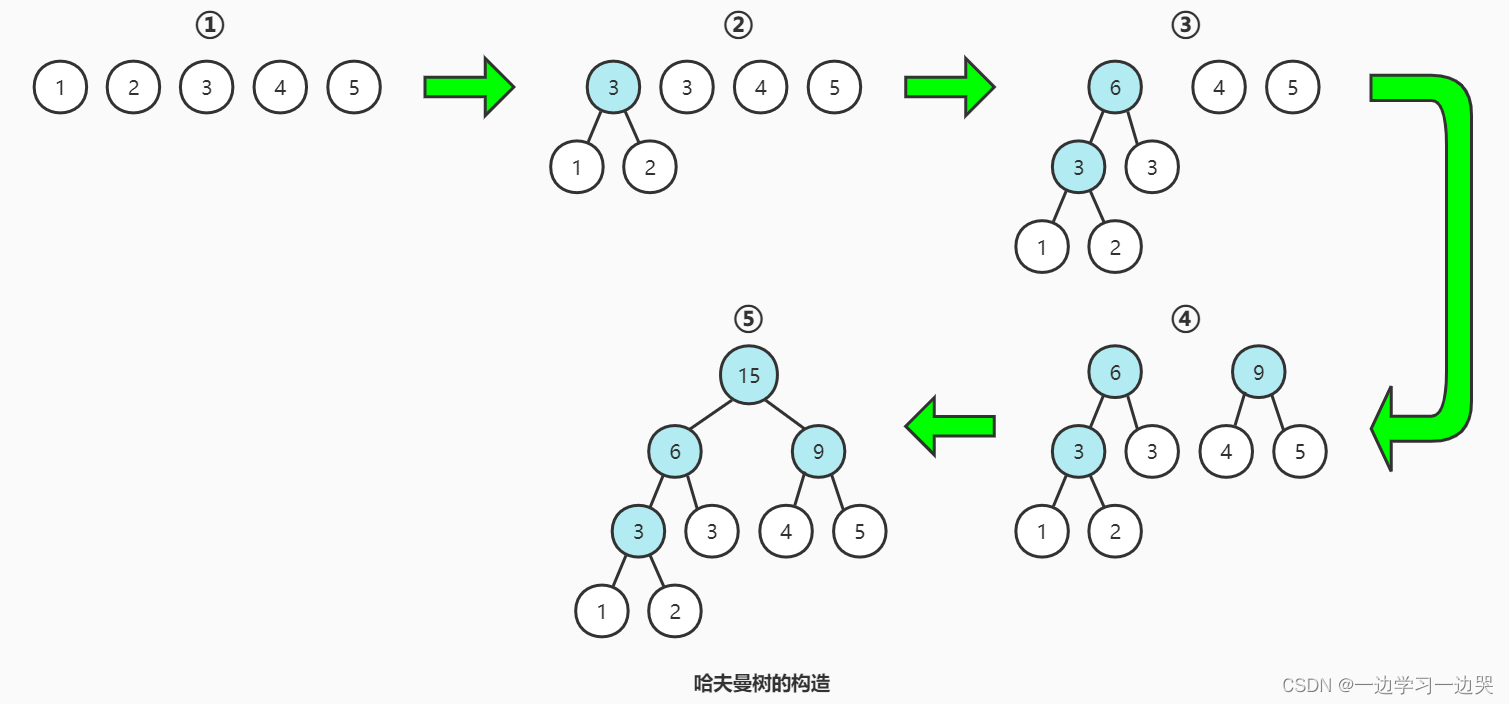
哈夫曼树构造的编码中，最主要的是“如何选择两个最小的结点？”。可以利用堆来解决，把结点的权值构造成最小堆，从里面挑两个最小的。

当然也可以用排序的方法来选择两个最小的结点，但是排序的方法效率不如堆。

哈夫曼树的特点

没有度为1的结点；
n个叶子结点的哈夫曼树公有2n-1个结点；
哈夫曼树的任意非叶结点的左、右子树互换后，任是哈夫曼树；
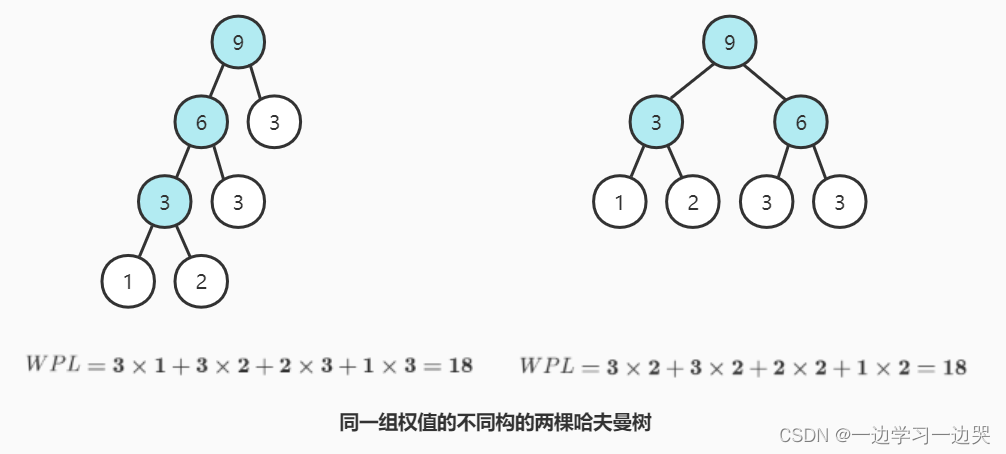
同一组权值，可能存在不同构的哈夫曼树。

一组权值{1,2,3,3}，不同构的两棵哈夫曼树：

哈夫曼编码

给定一段字符串，如何对字符进行编码，使得该字符串使用的编码存储空间最少？

【例】给定一段文本，包含58个字符，由以下7个字符构成：a，e，i，s，t，空格（sp），换行（nl）；这7个字符出现的次数不同。如何对字符进行编码，使得该字符串使用的编码存储空间最少？

【1.解决方法分析】

用等长ASCII编码（常规）：58 * 8 = 464位；
用等长3位编码（进阶）：58 * 3 = 174位（3位可以表示8个字符）；
不等长编码（最优）：出现频率高的字符用的编码短些；出现频率低的字符用的编码长些。

【2.遇到的问题】

如果使用方法3，则需要通过哈夫曼编码解决“编码问题”。

如果只是简单使用不等长编码对字符进行编码，如：“a: 1, e: 0, i: 10,s: 11...”。则10这个编码，既可以表示“ae”，也可以表示“i”。这里就会遇到编码的“二义性”。

【3.如何解决？】

3.1如何避免编码的二义性？

前缀码 prefix code：任何字符的编码都不是另一个字符编码的前缀。进行无二义地编码。

3.2用什么方式解决？

用二叉树进行编码（等长编码/不等长编码）

左、右分支分别由0和1表示；
字符只在叶子节点上。当所有字符都在叶结点上时，就不可能出现一个字符的编码是另一个字符编码的前缀。

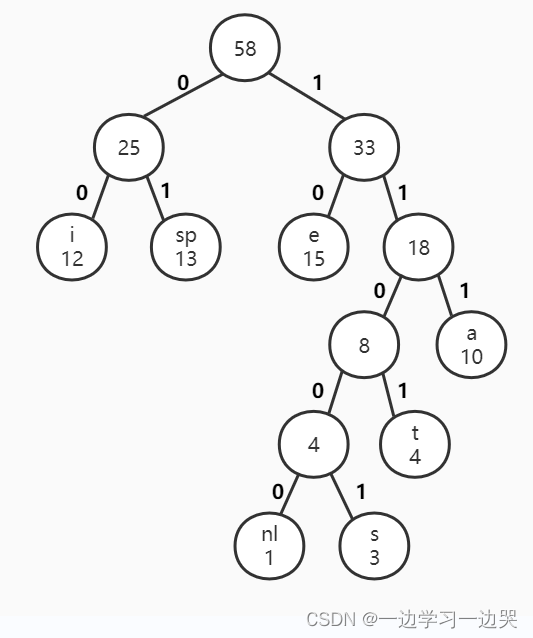
【4.不等长编码结果】

设字符出现频率：a: 10,e: 15, i: 12,s: 3,t: 4,sp:13,nl: 1

编码：

i: 00

sp: 01

e: 10

a: 111

t: 1101

nl: 11000

s: 11001

WPL = 12×2 + 13×2 + 15×2 + 10×3 + 4×4 + 3×5 + 1×5 = 146

【5.结论】

用等长ASCII编码（常规）：58 * 8 = 464位；
用等长3位编码（进阶）：58 * 3 = 174位；
不等长编码（最优）：146位。

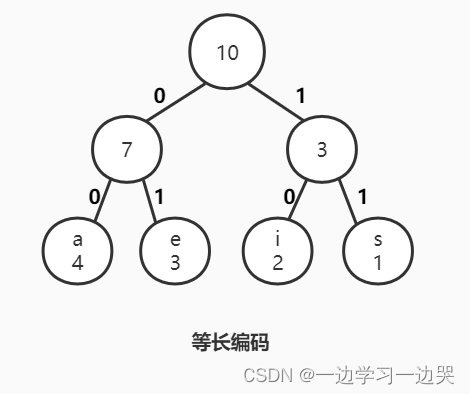
等长编码和不等长编码

设四个字符的频率：a: 4, e: 3, i:2, s:1

二叉树进行编码-等长码

编码：a: 00, e: 01, i: 10, s: 11

代价：4×2 + 3×2 + 2×2 +1×2 = 20

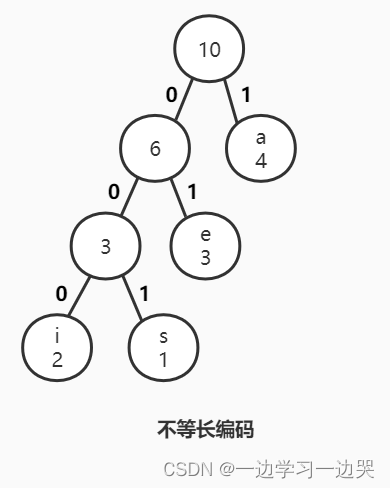
二叉树进行编码-不等长码

编码：a: 1,e: 01,i: 000,s: 001

代价：4×1 + 3×2 + 2×3 + 1×3 = 19