NLP中基本概念入门

词向量（Word Embedding）

  词向量主要用于将自然语言中的词符号数学化，这样才能作为机器学习问题的输入。

  数学化表示词的方式很多，最简单的有独热编码，即“足球”=[0,0,1,0,0,0,0,…]，“篮球”=[0,0,0,0,0,1,0,…]，向量的长度为总词数。显然，独热编码有以下缺点：1.可能导致维数过大，对深度学习来说复杂度过高。2.两个词的相似程度无法表示。

  词向量与独热编码不同，一般是以下形式：[0.2333,0.4324,0.6666,-0.9527,….]，维数以50维和100维比较常见。词向量解决了维度过大的问题，且两个词的相似度可以用欧几里得距离，余弦相似度等方法求得。

---

语言模型

  语言模型形式化的描述就是，给定一个字符串，看它是自然语言的概率P(w1,w2,…,wt)，其中wi表示这句话中的各个词。有个很简单的推论：

   P(w1,w2,…,wt)=P(w1)×P(w2|w1)×P(w3|w1,w2)×…×P(wt|w1,w2,…,wt−1)。

  而事实上，常用的语言模型都是在近似地求P(wt|w1,w2,…,wt-1)。比如n-gram模型就是用P(wt|wt-n+1,…,wt-1)近似表示前者。

---

分类器衡量指标

  以信息检索为例，总共50篇文献，其中20篇是我感兴趣的目标文献。输入特定检索条件返回10篇文献，其中5篇是我要的文献。那么：

  精确率(Precision) = 查出的文章中有多少是正确目标 = 5/10

  召回率(Recall) = 总共正确的文章中有多少被正确查出 = 5/20

  两种值都是我们想要提高的，但不能两全其美：想要精确率为1，最好的结果就是一篇文献也没搜到，返回的结果肯定没有分类错误，但这样也没有意义；想要召回率为1，最好的情况就是50篇 返回，这样搜索本身也失去了意义。

  定义F1分数为精确率与召回率的调和平均数：

$$F_1=\frac{2}{\frac{1}{Precision}+\frac{1}{Recall}}$$
  这样可以避免出现精确率和召回率一个为1一个为0的极端情况出现。

  还可以根据对精确率/召回率的不同偏好设置F_beta分数

$$F_\beta=\frac{(1+\beta^2)}{\frac{1}{Precision}+\frac{\beta^2}{Recall}}$$

  下面我们从另一个角度来看这个问题。假设我们现在要判断一个用户是好人还是坏人，定义：TP（True Positive）为预测正确的好人的个数，FP（False Positive）为预测错误的好人的个数，FN（False Negative）为预测错误的坏人的个数，TN（True Negative）为预测正确的坏人的个数。可以写出混淆矩阵（Confusion matrix）如下：

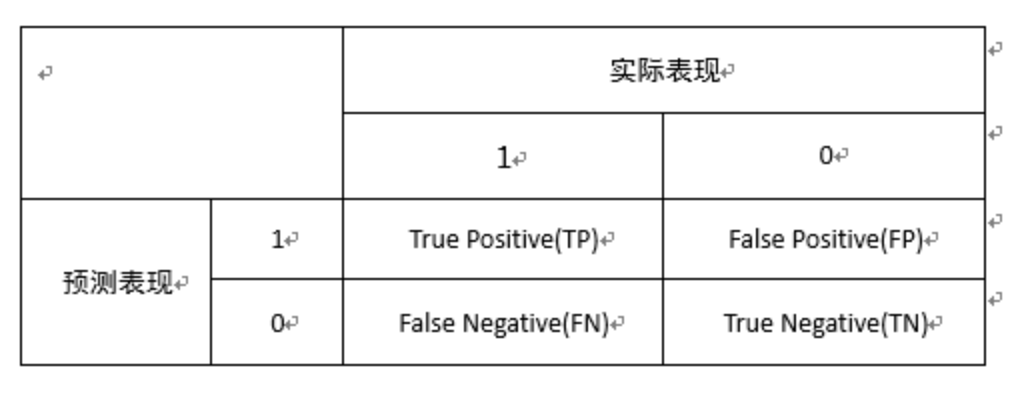
那么：

$$精确率(Precision)=\frac{TP}{TP+FP}$$

$$召回率(Recall)=\frac{TP}{TP+FN}$$