整数划分问题
将正整数n表示成一系列正整数之和:

{6};
{5+1};
{4+2},{4+1+1};
{3+3},{3+2+1},{3+1+1+1};
{2+2+2},{2+2+1+1},{2+1+1+1+1};
{1+1+1+1+1+1}。
【分析】
我们采用递归的方法进行求解。
我们将正整数n可划分的最大加数n1不大于m的划分个数,记为p(n, m)。
① 当 n = 1 或者 m = 1 时, n = 1 即有 p(1, m),那么只有一种划分,就是 {1}; m = 1 即有 p(n, 1),也只有一种划分,就是{1 + 1 + 1 + …… + 1}(其中内含 n 个 1);
所以,p(n, m) = 1;
② 当 n = m 时,p(n, m) = p(n, n)。
我们讨论:当该划分中含n时,那么它的划分次数有 1 次,即 {n};
当该划分中不含n时,那么它的划分次数为 p(n, n – 1) (因为此时划分中的最大加数还有可能为n - 1)。
所以,p(n, m) = p(n, n) = 1 + p(n, n – 1);
③ 当 n < m时,由于此时的正整数n 在所有的划分中,至多只有一种划分的最大加数为 n,即不可能超过 n,也就是说不可能存在有比n还大的加数m 形成一个属于 n 的划分。
所以,此时 p(n, m) = p(n, n);
④ 当 n > m > 1时,
我们讨论:当该划分中含m时,那么它的划分次数为 p(n – m, m) (其中 n – m 表示除去这个划分中包含的m;此时划分中的最大加数还有可能为 m);
当该划分中不含m时,那么它的划分次数为 p(n, m – 1) (因为此时的划分最大加数不可能为m,但有可能为 m – 1)。
所以,此时 p(n, m) = p(n – m, m) + p(n, m – 1)。
综上,我们可以得出p(n, m)的递推公式:
p(n, m) = 1 (n = 1 或者 m = 1)
p(n, m) = 1 + p(n, n – 1) (n = m)
p(n, m) = p(n, n) (n < m)
p(n, m) = p(n – m, m) + p(n, m – 1) (n > m > 1)
通过递推公式,我们就可以写出p(n, m)的递归方法,见源代码部分。
现在对方法p进行修改,使得p方法返回划分次数的同时还可以输出划分的结果(输出每种划分的可能形式)。将新的划分方法命名为partition1。
在输出一种划分结果,我们需要再增加一个int数组参数r,用来保存当前这种划分的每个加数;同时还需要增加一个int类型的参数pos,用来保存(指向)当前数组下一个可用的位置。
相对于p方法,partition1方法还要考虑的问题是在哪里输出划分的问题。假如输出的位置不正确的话就会导致输出结果的错乱。所以我们必须找到一个合适的输出位置。接下来我们就这问题进行讨论:
(提示:在每次成功构成一个新划分之后就可以进行输出)
当 n = 1时,pos指向的数组位置应该填入1,构成一个新的划分(因为当前划分还差1);
当 m = 1时,当前划分还需填入n个1,之后将构成一个新的划分;
当 n = m时,有两个情况:
第一种是,该划分包含m,即m加入数组后将构成一个新的划分,
(这里需要注意的是pos要进行还原操作,即指向原来的位置,因为此时要依靠
原来的数重新构建划分。如果不理解的话,可以看下面的源代码部分)
第二种是,该划分不包含m,此时还未形成一个新的划分,需要继续递归;
当 n < m时,同样不需要考虑,而是继续进行递归;
当 n > m > 1时,有两种情况:
第一种是,划分中包含m,即将m加入到数组中,并将指针pos后移,此时继
续进行递归;
(同样这里也需要对pos进行还原操作)
第二种是,划分中不包含m,那么此时继续进行递归。
综上,我们只要在p方法中适当加入构造划分的操作和输出操作就可以输出所有的划分形式了。(输出结果:所有划分出现的同一行,划分次数在行末)partition1方法的具体实现见源代码部分。
最后,我们再来讨论一下,所有划分的输出问题:例如我们输入6时,将会出现这样的输出结果:
现在我们对partition1方法进行进一步的修改,并将新修改的后的方法命名为partiton2。在新方法中,需要加入新的参数记录上一个划分的第一个数的值。我们可以得到,当划分的第一个数相同时,我们将这个划分放置在同一行进行输出;当当前的划分的第一个数不等于上一次划分的第一个数时,就进行换行。(这个参数的初始值可以设为0)这个新参数可以为含一个元素的数组,因为该参数将影响每一层的递归(如同C++中的全局变量)。具体实现见源代码部分。
【程序】
用java语言编写程序,代码如下:
import java.io.BufferedInputStream;
import java.util.Scanner;
public class Partition {
public static void main(String[] args) {
Scanner input = new Scanner(new BufferedInputStream(System.in));
while(input.hasNext()) {
int n = input.nextInt();
//System.out.println(p(n, n));
int[] r = new int[n];
int[] lastFirst = new int[1];
lastFirst[0] = 0;
System.out.println(partition2(n, n, r, 0, lastFirst));
//System.out.println(partition1(n, n, r, 0));
}
}
public static int p(int n, int m) {
if((n < 1) || (m < 1)) return 0;
if((n == 1) || (m == 1)) return 1;
if(n == m) return 1 + p(n, m - 1);
if(n < m) return p(n, n);
return p(n - m, m) + p(n, m - 1);
}
//partition方法版本1(增加划分输出,在一行中输出所有划分)
public static int partition1(int n, int m, int[] r, int pos) {
if((n < 1) || (m < 1)) return 0;
if((n == 1) || (m == 1)) {
for(int i = 0; i < n; i++) {
r[pos++] = 1;
}
output(r, pos);
return 1;
}
if(n == m) {
int p1 = 1;
r[pos++] = m;
output(r, pos);
pos--;
return 1 + partition1(n, m - 1, r, pos);
}
if(n < m) return partition1(n, n, r, pos);
r[pos++] = m;
int p1 = partition1(n - m, m, r, pos);
pos--;
int p2 = partition1(n, m - 1, r, pos);
return p1 + p2;
}
//partition方法版本2(修改输出效果)
//增加一个参数,用于保存上个划分的第一个数,这样在输出当前划分前就可以进行适当的换行或其他衔接操作。
//当当前的划分的第一个数与上一次相同的话,说明该划分将输出跟上次划分同一行。
//当当前的划分的第一个数与上一次不相同的话,说明该划分将进行换行操作。
public static int partition2(int n, int m, int[] r, int pos, int[] lastFirst) {
if((n < 1) || (m < 1)) return 0;
if((n == 1) || (m == 1)) {
for(int i = 0; i < n; i++) {
r[pos++] = 1;
}
if(r[0] == lastFirst[0])
System.out.print(",");//输出在同一行
else
if(pos != 1)//判断是否只有一个数。我们要确保不是第一个划分的输出。
System.out.println(";");
output(r, pos);//输出一个完整的划分
//为了影响原来的lastFirst变量,所以该为数组进行存储。充当类似C++中的全局变量。
lastFirst[0] = r[0];
//当当前划分的第一个数为1时,说明该划分为最后一个划分(由n个1组成),进行最后的换行操作
if(r[0] == 1)
System.out.println("。");
return 1;
}
if(n == m) {
//划分中含m的情况:
int p1 = 1;
r[pos++] = m;
if(r[0] == lastFirst[0])
System.out.print(",");
else
if(pos != 1)
System.out.println(";");
output(r, pos);
lastFirst[0] = r[0];
pos--;//注意需要将pos该为原来的值
//划分中不含m的情况:partition2(n, m - 1, r, pos, lastFirst)
return 1 + partition2(n, m - 1, r, pos, lastFirst);
}
if(n < m) return partition2(n, n, r, pos, lastFirst);
//划分中含m的情况:
r[pos++] = m;
int p1 = partition2(n - m, m, r, pos, lastFirst);
pos--;//回到原来的值
//划分中不含m的情况:
int p2 = partition2(n, m - 1, r, pos, lastFirst);
return p1 + p2;
}
//用数组r进行存储划分中的每个数,输出划分结果
public static void output(int[] r, int len) {
System.out.print("{" + r[0]);
for(int i = 1; i < len; i++)
System.out.print("+" + r[i]);
System.out.print("}");
}
}
【运行结果】
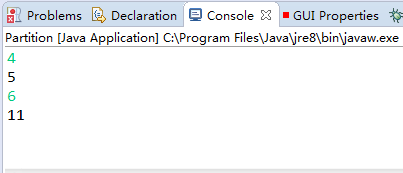
依次输入5, 6,p方法的输出结果:
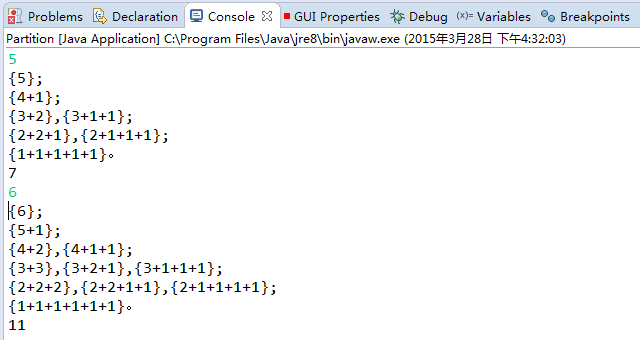
依次输入5,6,partition1方法的输出结果:

依次输入5,6,partition2方法的输出结果:
【体会】
在此之前我们需要写出递推公式,那么我们就可以根据递推公式写出递归方法。此外,当一个方法很复杂时,我们所要做的是先将简单的方法写出来再进行下一步的扩充。例如在这道题,我并不是直接写出最终的partition2这个方法,而是基于可以输出所有划分次数的p方法和可以在一行输出所有划分结果和划分次数的partition1方法进行扩充而来的。由此,我们也可以知道一个方法来自于不同的方法结构组成,当这个方法可以拆分成几个简单方法或者可以由简单方法进行扩充时,我们采取分步实现将有利于我们的编程。此外,还有一点,就是我们在编写递归方法时,我们应该学会更多地从宏观的角度去看待这个递归问题,否则将容易使自己的思绪陷于递归的“泥沼”。








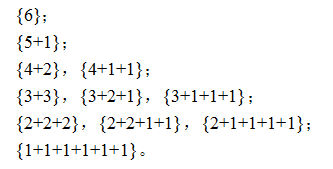
























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








