对PCA降维的理解

对PCA降维的理解

　　这几天要参加数学建模了，突然想起在建模中可能会遇到从大量的特征指标中选出关键特征的这个工作，有可能会用到PCA降维的知识，所以在比赛前又对这个知识点做一番整理。
　　这篇博客的首要目的是说明PCA的降维原理。示例方面的话在之后有时间就进行补充。我的叙述会以以下顺序进行。

1. 向量空间
2. 线性映射
3. 减少纬度间的相关性
4. 求得特征值与特征向量
5. 获得线性映射空间

1、向量空间

向量空间是由向量组成的空间。向量空间存在的前提是有一组基向量。在这个空间中的向量都可以由这组向量表示。我们常见的二维空间就是由两个相互正交的向量为基向量的向量空间：

[1,2]*[x,0] ^T＝［x,0］　&&　[1,2]*[0,y]=[0,2y]　　　　　　　　　　　　　　(1)
这里的[1,2]是这个二维空间中的一个向量，[x,0],[0,y]是这个空间的一组基向量。而[1,2]在这两维上的投影是x与2y，为了方便起见，我们的x与y一般都取到单位“1”。
由一组基向量组成的线性空间我们已经生成好了，那么我们如何把一个向量映射到这个空间中来呢？–》线性映射

2、线性映射

线性映射（linear transformation ）是从一个向量空间V到另一个向量空间W的映射且保持加法运算和数量乘法运算，而线性变换（linear mapping）是线性空间V到其自身的线性映射。—-百度百科

　已知A=[a1,a2,a3,a4,a5]^T是由5个n(n>5)维行向量组成的矩阵。有个n维向量b:
　A*b — 由矩阵相乘规则是一个5维的向量，这个时候我们可以认为b向由A矩阵表示的向量空间(a1,a2,a3,a4,a5)做了映射，结果维度从原来自己的n维降到了5维。这里我们从原来的n维空间到5维是做了一次线性映射。
　此处需要作图：

3、减少维度间的相关性

既然如此，将高维映射到低维如此简单，那么我们的思考的重点应该放在如何选取这个重要的基坐标上。在这个问题上，我们又得分为三部分讲述，但是我不分了，真取用最少的篇幅讲完：
　　　我们首先从宏观的视角看待这个问题。在高维映射到低维的过程中，数据信息的损失在所难免，但是如何选取较少的维度，表示足够多的信息呢？（1）这里我们需要引入统计学中的一个概念，叫做方差。方差越大表示数据波动越大，包含的信息量越大。反之也不难理解。（2）另外我们需要考虑的一点是，在低维空间中，不同维度之间应该尽可能的线性无关，也即样本不同维度的协方差应该为0，维度的使用率尽可能的高，我们如果两个维度相关的话，会有一部分内容重复，导致信息的表达不充分。由此我们可以有如此做法：
　　 ————方差
　　
—————协方差

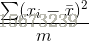
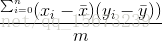
　B=[b1,b2,b3,b4,b5] 　C = B^TB.
这里B是样本组成的矩阵，C的对角线是样本值B的方差，非对角线上的元素是协方差值。于是乎我们现在得到了一组由样本方差与协方差组成的矩阵C。我们接下来的目标就是把C中的协方差最小化为0。我们可以如下做。使用特征值与特征变量将该矩阵化为一个对角线上元素不全为0，而非对角线的元素全是0。

4、求得特征值与特征向量　

由于C为一个nxn的对称矩阵，所以一定存在正交基P，与对角矩阵V满足以下公式：　

C = P ^TVP
这里的V是由特征值组成的对角矩阵。P是由特征向量组成的基向量。亦即我们所求的特征空间。

5、获得线性映射空间　

最后我们所需要做的线性映射是D=P^TB；