小波变换基础分析

概念回顾：

• 基（$basis$）：在线性代数中我们都曾学过，它表示空间中的一系列线性独立的向量，空间中的其他向量都可以通过它的线性组合表示。在傅里叶变换中是无限长的三角函数基，在小波变换种是有限长的会衰减的小波基

• 变换：不管是压缩、滤波还是图像处理，本质都是变换，就是基。例如傅里叶变换就是将信号用该空间的基的线性组合进行表示。

• 正交：在$Hilbert$空间种用来刻画两个向量的夹角，当内积为$0$时，两个向量正交.如果两个向量的内积为$0$，它们就是正交的；如果一个向量序列相互对偶正交，并且长度为$1$，它们就是正交归一化的。

FFT函数需要了解的知识点

• 频谱关于中间位置对称，只需要观察 0:1：N/2（这N/2+1个点）（时域采集N个点，频域只需要观察N/2+1个点）

• MATLAB中FFT的频谱，应该看幅值

• X轴频率点的设置：采样频率为Fs,频谱图显示的最高频率为Fs/2（采样定理）：X轴频率点：（0:1：N/2）*Fs/N

• 复数幅值修正

  复数序列Y的幅值，需要进行转换，才能得到与时域中对应信号值的幅值。具体计算公式如下：
  $$修正后的幅值=\{\begin{array}{l}\frac{2\ast Y的幅值}{N}，(当频率介于0Fs/2时)\\ \frac{Y的幅值}{N}，(当频率等于0或者Fs/2时)\end{array}$$

• 画出的频谱图的频率分辨率为Fs/N

• 采样频率Fs大于信号最大频率的的2倍

• 由于采样定理可知，当不满足采样定理的时候将出现混叠现象，所以FFT处理时默认$Fs/2$为最高信号频率
  假设采样频率为Fs，信号频率F，采样点数为N。那么FFT之后结果就是一个为N点的复数。每一个点就对应着一个频率点。这个点的模值，就是该频率值下的幅度特性。具体跟原始信号的幅度有什么关系呢？假设原始信号的峰值为A，那么FFT的结果的每个点（除了第一个点直流分量之外）的模值就是A的N/2倍。而第一个点就是直流分量，它的模值就是直流分量的N倍。而每个点的相位呢，就是在该频率下的信号的相位。

小波变换与傅里叶变换

傅里叶变换本质上是用在两个方向上都无限伸展的正弦曲线作为正交基函数，把周期函数展成傅里叶级数，把非周期函数展成傅里叶积分，利用傅里叶变换对函数做频谱分析，反映整个信号的时间频谱特性，较好的揭示平稳信号的特征。具体来说，傅里叶变换是通过将一个信号和一系列频率不同的正弦波相乘，就能够确定信号中存在哪些频率。如果信号中的某个频率和正弦波之间的点积（用于衡量两个向量/信号重叠的程度）导致振幅很大，就意味着这两个信号之间有很多的重叠，信号中就包含这个特定的频率。

但是傅里叶变换存在的一个问题就是，它只能告诉我们有哪些频率，却无法准确的告诉我们这些频率存在的具体的时间点。如下图所示，两个不同的时序信号使用傅里叶变换处理后，得到了右边对应的频谱图，从中我们可以看出虽然原始信号有很明显的差距，第一个信号中存在四个不同的频率$（4、30、60、90）$。这些频率在任何时刻都存在，而在下面的第二个信号中四种频率是依次出现的。有趣的是表现在频谱图中却很相近，因为他们的有一样的频率，表现在图上即有相同的四个峰。所以通过傅里叶变换，有时我们无法识别两个相差很大的信号 。

#python代码：
t_n = 1
N = 100000
T = t_n / N
f_s = 1/T
 
xa = np.linspace(0, t_n, num=N)
xb = np.linspace(0, t_n/4, num=N/4)
 
frequencies = [4, 30, 60, 90]
y1a, y1b = np.sin(2*np.pi*frequencies[0]*xa), np.sin(2*np.pi*frequencies[0]*xb)
y2a, y2b = np.sin(2*np.pi*frequencies[1]*xa), np.sin(2*np.pi*frequencies[1]*xb)
y3a, y3b = np.sin(2*np.pi*frequencies[2]*xa), np.sin(2*np.pi*frequencies[2]*xb)
y4a, y4b = np.sin(2*np.pi*frequencies[3]*xa), np.sin(2*np.pi*frequencies[3]*xb)
 
composite_signal1 = y1a + y2a + y3a + y4a
composite_signal2 = np.concatenate([y1b, y2b, y3b, y4b])
 
f_values1, fft_values1 = get_fft_values(composite_signal1, T, N, f_s)
f_values2, fft_values2 = get_fft_values(composite_signal2, T, N, f_s)
 
fig, axarr = plt.subplots(nrows=2, ncols=2, figsize=(12,8))
axarr[0,0].plot(xa, composite_signal1)
axarr[1,0].plot(xa, composite_signal2)
axarr[0,1].plot(f_values1, fft_values1)
axarr[1,1].plot(f_values2, fft_values2)
(...)
plt.tight_layout()
plt.show()

为了解决这个无法分辨频率出现时间的问题，提出了短时傅里叶变换$（Short-TimeFouierTransform）$，它的主要思想是在使用傅里叶变换前，通过相同的滑动窗口将原始的信号分割成几部分相等长度的信号（可能有重叠部分），在这些小的部分，将其看成近似平稳的信号，然后再使用傅里叶变换，这样我们不仅可以知道信号中存在哪些频率，而且还知道它们出现的时间点。例如假设我们将其分割为$10$部分，如果后面使用的傅里叶变换在第二部分探查到一种特殊的频率，我们就可以根据这个信息知道它存在于原始信号的$2/10$和$3/10$的中间部分。

但是短时傅里叶变换也存在一个问题：我们无法确定使用多宽的窗口得到最好的效果。如果窗口窄会使得窗内的信号太短，对于频率的分析不够准确，频率的分辨率低；而窗口太大时域上又不太精细，时间的分辨率低。理论上分时间辨率高、频率分辨率低的适合窄窗口，而时间分辨率低、频率分辨率高的适合宽窗口，但是在短时傅里叶变换中，窗口的大小是固定的，所以它还是不能很好的满足非稳定信号的处理需求。

为了解决短时傅里叶变换中出现的问题，就出现了小波变换$（WaveletTransform）$，它在时域和频域上都有相当高的分辨率，不仅可以告诉我们信号中存在哪些频率，同时还能告诉不同频率出现的具体时刻。这通过使用不同的缩放实现。

关于小波变换的描述如下：小波变换$（wavelettransform，WT）$是一种新的变换分析方法，它继承和发展了短时傅立叶变换局部化的思想，同时又克服了窗口大小不随频率变化等缺点，能够提供一个随频率改变的“时间-频率”窗口，是进行信号时频分析和处理的理想工具。它的主要特点是通过变换能够充分突出问题某些方面的特征，能对时间（空间）频率的局部化分析，通过伸缩平移运算对信号（函数)逐步进行多尺度细化，最终达到高频处时间细分，低频处频率细分，能自动适应时频信号分析的要求，从而可聚焦到信号的任意细节，解决了$Fourier$变换的困难问题，成为继$Fourier$变换以来在科学方法上的重大突破。

从上图我们可以看到不同的变换方式在时间分辨率和频率分辨率的差别，块的大小和方向表明了在时域和频域中我们能分辨的最小的特征。如图所示的原始信号中，时域的分辨率高，频域分辨率为零，意味着我们可以在时域中分辨出非常小的特征，而在频域中没有特征。而傅里叶变换在频域具有高分辨率，在时域具有零分辨率。短时傅里叶变换相对于上面的两种方法，它在时域和频域具有中等的分辨率。

而小波变换有如下的特点：
• 对于小频率值，频域分辨率高，时域分辨率低
• 对于大频率值，频域分辨率低，时域分辨率高

小波变换在频域分辨率和时域分辨率两者之间做了权衡：在与时间相关的特征上，它在时域具有高分辨率；而在与频率相关的特征上，它在频域具有高分辨率。

小波变换工作原理

​ 傅里叶变换使用了一系列不同频率的正弦波去分析信号，即将原始信号表示为一系列正弦波的线性组合。而小波变换使用了一系列称为小波的函数，每个小波都具有不同的尺度。

从上图我们可以看出，小波相比于正弦波的最大的一个特点就是关于时间它有很好的局部性，而正弦波在时域上是没有这个特点的（它从负无穷延申到正无穷），这就决定了小波变换可以获得除频率信息外更加准确的时间信息。借助小波变换在时间上具有局部性的这个优点，我们可以将信息的不同时间的部分与小波进行相乘，从信号的开始处，慢慢的移到信号的末尾，这个过程也成为卷积（convolution）。在我们对原始信号（也称母小波）进行这些操作后，可以对它进行缩放，使它变得更大，不断重复这个过程。

一维信号的小波变换具有二维特征，这种二维小波变换的输出是以尺度图的形式表示信号的时间尺度。这个维度叫什么?由于傅里叶变换保留了频率，所以小波变换通常用尺度$（scale）$来表示。这就是为什么尺度图的两个维度是时间和尺度。如果频率比尺度更加直观的话，可以使用下面的公式将其转换成伪频率$（pseudo-frequencies）$。
$$f_a=\frac{f_c}{a}$$

其中$f_a$就是最后的伪频率，$f_c$是母小波的中心频率，$a$ 是缩放因子。

我们可以使用一个更大的尺度因子(更长的小波)来对应一个更小的频率，通过对小波在时域进行尺度变换，我们可以在频域中分析更小的频率(获得更高的分辨率)。反之通过使用更小的尺度，我们在时域中有了更多的细节。所以尺度基本上是频率的倒数（在$PyWavelets$中使用$scale2frequency$来完成尺度域到频率域的转换）。

小波变换的另一个优点是它可以很好的处理突变信号，对于傅里叶变换来来说，在处理突变信号时存在吉布斯效应（对于这种变换突然而剧烈的信号，即使只有一小段变换，傅里叶变换也不得不用大量的三角波去拟合）

不同类型的母小波

不同于傅里叶变换只有正弦波，小波变换有许多不同类型的小波。小波族之间的不同，来自于对小波紧凑性和平滑性的权衡，它方便了我们根据自己的任务，从中选择特定的小波，在信号中寻找特征。

在$PyWavelets$库中有如下的14种母小波，每种类型的小波都有不同的形状、平滑度和紧凑性，用于不同的目的。因为小波只需满足两个数学条件（归一化约束和正交约束），所以我们很容易构造一种新的小波。

小波必须有如下的的条件：
• 有限的能量
• 均值零
• 可以正交也可以不正交
• 可以是双正交的，也可以不是
• 可以是对称的，也可以不是
• 可以是负数，也可以是实数
• 如果它是复数，通常分为表示振幅的实部和表示相位的虚部
• 被归一化为单位能量

第一个条件意味着它在时间和频率上具有局部性的;它是可积的，小波与信号的内积始终存在。第二个条件意味着小波在时域中均值为零，在时域中频率为零时均值为零。这对于保证小波变换的可积性和计算小波变换的逆是必要的。

下图是几个不同的小波族的图，第一行包含四个离散小波，第二行包含四个连续小波。可在

discrete_wavelets = ['db5', 'sym5', 'coif5', 'bior2.4']
continuous_wavelets = ['mexh', 'morl', 'cgau5', 'gaus5']

list_list_wavelets = [discrete_wavelets, continuous_wavelets]
list_funcs = [pywt.Wavelet, pywt.ContinuousWavelet]

fig, axarr = plt.subplots(nrows=2, ncols=4, figsize=(16,8))
for ii, list_wavelets in enumerate(list_list_wavelets):
    func = list_funcs[ii]
    row_no = ii
    for col_no, waveletname in enumerate(list_wavelets):
        wavelet = func(waveletname)
        family_name = wavelet.family_name
        biorthogonal = wavelet.biorthogonal
        orthogonal = wavelet.orthogonal
        symmetry = wavelet.symmetry
        if ii == 0:
            _ = wavelet.wavefun()
            wavelet_function = _[0]
            x_values = _[-1]
        else:
            wavelet_function, x_values = wavelet.wavefun()
        if col_no == 0 and ii == 0:
            axarr[row_no, col_no].set_ylabel("Discrete Wavelets", fontsize=16)
        if col_no == 0 and ii == 1:
            axarr[row_no, col_no].set_ylabel("Continuous Wavelets", fontsize=16)
        axarr[row_no, col_no].set_title("{}".format(family_name), fontsize=16)
        axarr[row_no, col_no].plot(x_values, wavelet_function)
        axarr[row_no, col_no].set_yticks([])
        axarr[row_no, col_no].set_yticklabels([])
plt.tight_layout()
plt.show()

在每个小波族中，可以有许多不同的子小波。可以通过系数的数量(如消失矩的数量)和分解的级别来区分小波的不同的子小波。下面的这个小波族称为$“Daubechies”$。从图中我们可以看到，在第一列中，我们可以看到一阶$(db1)$的$Daubechies$小波，在二阶$(db2)$的第二列中，一直到第五列中的第五阶。小波包含多达20阶$(db20)$的$Daubechies$小波。

阶数表示消失力矩的个数。所以$db3$有3个消失力矩$db5$有5个消失力矩。消去矩的个数与小波的逼近阶数和平滑度有关。如果一个小波有p个消失矩，它可以近似p - 1次多项式。

在选择小波时，我们还可以指出分解的级别。默认情况下，$PyWavelets$为输入信号选择可能的最大分解级别。分解的最大级别(参见$pywt.dw{t}_{m}a{x}_{l}evel()$)取决于输入信号长度和小波的长度。

可以看出，随着消失矩数的增加，小波的多项式阶数增加，小波变得更加平滑。随着分解程度的增加，这个小波的样本数以增加的形式表示。
所有小波基库图表：

小波变换有连续小波变换（Continuous Wavelet Transform）和离散小波变换（Discrete Wavelet Transform）种风格。离散小波变换在尺度和平移域上是离散的，但在时域上不是离散的。为了能够处理数字和离散信号，我们还需要在时域对小波变换进行离散化。这些形式的小波变换分别称为离散时间小波变换（Discrete-Time Wavelet Transform）和离散时间连续小波变换（Discrete-Time Continuous Wavelet Transform）。

多级离散小波变换（DWT是一个滤波器组）

在实践中，DWT总是作为一个过滤器库来实现。这意味着它被实现为高通滤波器和低通滤波器的级联。这是因为滤波器组是一种非常有效的方法，将一个信号分解成几个子频带。

在信号数据上使用DWT，我们从最小的尺度开始,小尺度对应高频，这意味着我们首先分析高频行为。在第二阶段，尺度随大小为2的因子的增大而增大(频率随因子的减小而减小)，我们分析的是最大频率的一半左右的行为。在第三阶段，尺度因子为4，我们正在分析最大频率的四分之一左右的频率行为。这样一直进行下去，直到达到最大分解水平。

那么什么是最大分解水平?为了理解这一点，我们还应该知道，在随后的每个阶段，信号中的样本数量都减少了一倍。在较低的频率值，你将需要更少的样本，以满足奈奎斯特率，所以没有必要保持较高的样本数量的信号;它只会导致转换的计算开销。由于这种向下采样，在这个过程的某个阶段，我们的信号中样本的数量将小于小波滤波器的长度，我们将达到最大的分解水平。
举个例子，假设我们有一个频率高达$1000hz$的信号。在第一个阶段，我们把信号分成低频部分和高频部分，即$0-500hz$和$500-1000hz$。在第二阶段，我们取低频部分，再次将其分为两部分:$0-250hz$和$250-500hz$。在第三阶段，我们将$0-250hz$的部分为$0-125hz$的部分和$125-250hz$的部分。这种情况会一直持续下去，直到我们达到了所需的精化水平，或者直到我们的样本耗尽为止。

通过将DWT应用于chirp signal，我们可以很容易地将这个想法形象化。chirp signal是具有动态频谱的信号;频谱随时间而增加。信号的开始包含低频值，信号的结束包含高频值。这使得我们很容易通过简单地观察时间轴来直观地看到频谱的哪一部分被过滤掉了。

x = np.linspace(0, 1, num=2048)
chirp_signal = np.sin(250 * np.pi * x**2)
    
fig, ax = plt.subplots(figsize=(6,1))
ax.set_title("Original Chirp Signal: ")
ax.plot(chirp_signal)
plt.show()
    
data = chirp_signal
waveletname = 'sym5'
 
fig, axarr = plt.subplots(nrows=5, ncols=2, figsize=(6,6))
for ii in range(5):
    (data, coeff_d) = pywt.dwt(data, waveletname)
    axarr[ii, 0].plot(data, 'r')
    axarr[ii, 1].plot(coeff_d, 'g')
    axarr[ii, 0].set_ylabel("Level {}".format(ii + 1), fontsize=14, rotation=90)
    axarr[ii, 0].set_yticklabels([])
    if ii == 0:
        axarr[ii, 0].set_title("Approximation coefficients", fontsize=14)
        axarr[ii, 1].set_title("Detail coefficients", fontsize=14)
    axarr[ii, 1].set_yticklabels([])
plt.tight_layout()
plt.show()

Sym 5小波(1 - 5级)的近似和细节系数应用于chirp signal信号(1 - 5级)。在左边，我们可以看到一个示意图表示的高通和低通滤波器应用于信号的每一级。其中还需知道如下：
• 在PyWavelets中，DWT由pywt.dwt()实现
• DWT返回两组系数;近似系数和细节系数
• 近似系数表示小波变换的低通滤波器(平均滤波器)的输出
• 细节系数表示小波变换的高通滤波器(差分滤波器)的输出
• 通过对上一级小波变换的近似系数进行小波变换，得到下一级小波变换
• 每下一层，原始信号的采样率也下降2倍

DWT作为多级滤波器库的含义：在随后的每一级，近似系数被划分为较粗的低通和高通部分，并在低通部分再次应用DWT。我们可以看到，我们的原始信号现在被转换成几个信号，每个信号对应不同的频段。这种在不同尺度上分析信号的思想也称为多分辨率/多尺度分析，以这种方式分解信号也称为多分辨率分解，或子带编码。

总体来说小波变换具有如下的优点：
• 可以覆盖整个频域
• 通过选择合适的滤波器，可以极大的减小或去除所提取不同特征之间的相关性
具有“变焦”的特性，可以根据频率的高低调整窗口，在低频可用高频率分辨率和低时间分辨率，在高频段可用低频率分辨率和高时间分辨率

五个简单的步骤的做连续小波变换：

连续小波变换

１． 取一个小波，　把它和信号的开始点做比较。

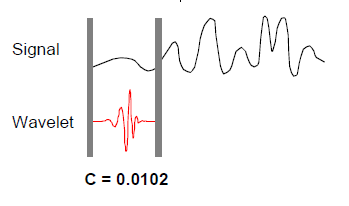
２． 计算一个数，c, 代表小波和这个区域内的信号有多接近，　c越近，相似度越

高。这完全取决于你选择的小波形状

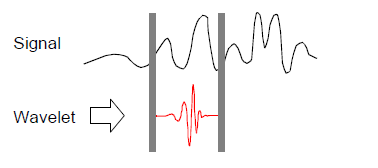
３． 位移小波，　重复１２　，直到你完全运算完整个信号。

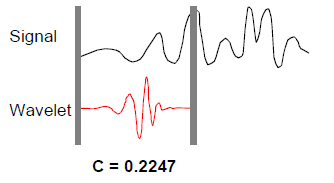
４．　缩小或者伸展真整个小波，　重复１，２，３

5． 循环执行上述四个步骤，直到满足分析要求为止。

小波变换案例分析：

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%画信号的幅频谱和功率谱
%频谱使用matlab例子表示
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
function plot_fft(y,fs,style,varargin)
%当style=1,画幅值谱；当style=2,画功率谱;当style=其他的，那么花幅值谱和功率谱
%当style=1时，还可以多输入2个可选参数
%可选输入参数是用来控制需要查看的频率段的
%第一个是需要查看的频率段起点
%第二个是需要查看的频率段的终点
%其他style不具备可选输入参数，如果输入发生位置错误
nfft=2^nextpow2(length(y));%找出大于y的个数的最大的2的指数值（自动进算最佳FFT步长nfft）
%nfft=1024;%人为设置FFT的步长nfft
y=y-mean(y);%去除直流分量
y_ft=fft(y,nfft);%对y信号进行DFT，得到频率的幅值分布
y_p=y_ft.*conj(y_ft)/nfft;%conj()函数是求y函数的共轭复数，实数的共轭复数是他本身。
y_f=fs*(0:nfft/2-1)/nfft;%T变换后对应的频率的序列
% y_p=y_ft.*conj(y_ft)/nfft;%conj()函数是求y函数的共轭复数，实数的共轭复数是他本身。
if style==1
    if nargin==3
       plot(y_f,2*abs(y_ft(1:nfft/2))/length(y));%matlab的帮助里画FFT的方法
       ylabel('幅值');xlabel('频率/hz');title('信号幅频谱');
       %plot(y_f,abs(y_ft(1:nfft/2)));%论坛上画FFT的方法
    else
       f1=varargin{1};
       fn=varargin{2};
       ni=round(f1 * nfft/fs+1);
       na=round(fn * nfft/fs+1);
       plot(y_f(ni:na),abs(y_ft(ni:na)*2/nfft));
       ylabel('幅值');xlabel('频率/Hz');title('信号幅频谱');
    end
elseif style==2
           plot(y_f,y_p(1:nfft/2));
           ylabel('功率谱密度');xlabel('频率/Hz');title('信号功率谱');
    else
       subplot(211);plot(y_f,2*abs(y_ft(1:nfft/2))/length(y));
       ylabel('幅值');xlabel('频率/Hz');title('信号幅频谱');
       subplot(212);plot(y_f,y_p(1:nfft/2));
       ylabel('功率谱密度');xlabel('频率/Hz');title('信号功率谱');
end
end
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%对数据进行小波七层分解重构
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%%%%%%%%%%%
%调入含突变点的信号
%%%%%%%%%%%%%%%%%%%%%%%%%
load cnoislop;
x=cnoislop;
fs =2000;
d = 'db3';
N=length(x);
[c,l]=wavedec(x,7,d); %小波基为d:coif5,分解层数为7层 小波变换函数
ca11=appcoef(c,l,d,7); %小波变换低频部分系数提取
cd1=detcoef(c,l,1); %小波变换高频部分系数提取
cd2=detcoef(c,l,2); 
cd3=detcoef(c,l,3); 
cd4=detcoef(c,l,4); 
cd5=detcoef(c,l,5); 
cd6=detcoef(c,l,6); 
cd7=detcoef(c,l,7); 
sd1=zeros(1,length(cd1)); %设置成0阵
sd2=zeros(1,length(cd2)); %1-3层置0,4-5层用软阈值函数处理 5-7层用硬阈值函数处理
sd3=zeros(1,length(cd3)); 
sd4=wthresh(cd4,'s',0.014); %返回输入向量或矩阵X经过软阈值（如果SORH='s'）
sd5=wthresh(cd5,'s',0.014); %或硬阈值（如果SORH='h'）处理后的信号。T是阈值。
sd6=wthresh(cd6,'h',0.014); 
sd7=wthresh(cd7,'h',0.014); 
c2=[ca11,sd7,sd6,sd5,sd4,sd3,sd2,sd1]; 
s0=waverec(c2,l,'db3'); %小波重构 
figure; 
subplot(221);plot(x),title('原始数据小波去噪前'),xlabel('x','FontSize',15),ylabel('幅值','FontSize',15)
subplot(223);plot(s0),title('原始数据小波去噪后'),xlabel('x','FontSize',15),ylabel('幅值','FontSize',15)
subplot(222)
plot_fft(x,fs,1);%原图像对应频谱
subplot(224)
plot_fft(s0,fs,1);%原图像对应频谱