Educational Codeforces Round 133 (Rated for Div. 2) D. Chip Move （完全背包dp）

原题链接：Problem - D - Codeforces

题目大意:

        给出两个数 ， ，起点从下标  开始，第  步能跳的距离为  的倍数，即  步，第  步能跳的距离为  的倍数，即以此类推。要求你求出跳到区间  的方案数，答案对 取模。

解题思路：

        求方案数目，首先先想到dp。针对样例  ，我们先画图观察一下：

        首先，第  步选择跳跃的时候，我们能跳  的距离（红色为能跳到的地方）

 

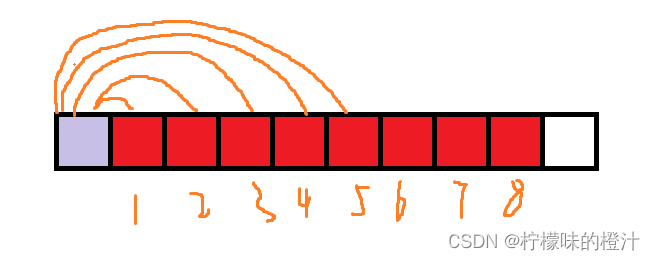
        第  步时候我们选择跳  的距离，我们就能去到下标  ，选择  的距离我们就能去到  。他们都为  的倍数，因此全部跳完之后，我们得到的结果就是图中红色标注的方格。

        继续跳第  步，看看会发生什么：

        我们首先选择跳  步，得到的结果如下：(用橙色点标出)

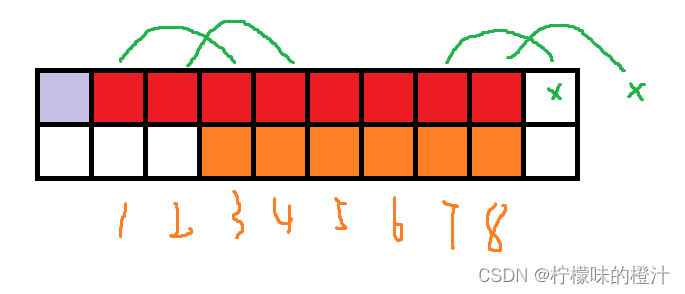
         解释一下，首先，我们要能跳第  步，那肯定从之前跳过了  步的点，继续往后跳。那么就是  跳到 ， 跳到 ...。由于  跳到了范围外了，所以我们不考虑进来。

        我们再选择跳  步，得到的结果如下：(用深绿色点标出)

         

        同理：从  跳到 ，从  跳到 ...得到的就是绿色的点。

        我们将所有第  步的选择跳完，得到的结果就是：

        

          这两个点，在所有第  步的选择中，只能去到  次， 能去  次， 能去  次。

        如果我们  枚举   （ 代表当前为第几步）的倍数，将所有能去到的点都  地扫一遍，总共要扫  次，总复杂度肯定会是  级别的，这是不可接受的。

        考虑完全背包的转移方程：

        

        取  个，个，个...个物品，我们完全可以用之前记录的取了  个物品的值，加上单个物品的值，即  ，最终得到取第  个的结果。我们可以利用完全背包来优化枚举倍数。

         假设状态  为当前准备跳第  步，下标  能够被跳到的总次数，那么转移方程就为：

        

        这样，复杂度就被压到了  的级别，似乎还过不了这题，我们仔细观察转移的情况。

        对于样例 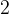，我们会得到这样一个图像：

        

        （左边代表第几步，上方代表得到的结果，下方代表下标）

        你会发现，事实上从第  步开，后面的步骤完全不用跳了。因为无论怎么跳，最多只能跳三步，再往后跳，也只会跳出范围。因此，事实上复杂度是跑不满  的，甚至和  差不多，我们只需要判断当前是否还有能跳的点，如果没有则直接 break 掉就可以了。

        空间是  的级别，那么我们开一个滚动数组就行了。

AC代码：

#include <bits/stdc++.h>
using namespace std;

using i64 = long long;
const int N = 3e5 + 10, mod = 998244353;
int dp[2][N];

void solve()
{
	int n, k, now = 0, pre = 1; //now为 i, pre则为i - 1
	cin >> n >> k;
	vector<int> ans(n + 1);//开一个ans来加上所有步的答案

	dp [pre][0] = 1;
	for (int i = k; i <= n; ++i)
	{
		bool ok = true;//利用ok来判断还能否继续跳

		for (int j = i; j <= n; ++j) 
		{
			dp[now][j] = (dp[now][j - i] + dp[pre][j - i]) % mod;
			if (dp[now][j]) ok = false;
		}

		if (ok) break;

		for (int i = 0; i <= n; ++i) 
			ans[i] = (ans[i] + dp[now][i]) % mod, dp[pre][i] = 0;
            //ans来加上所有步的答案 顺带把dp[i + 1][j]清零
		
		now ^= 1, pre ^= 1;//滚动
	}
	for (int i = 1; i <= n; ++i) cout << ans[i] << ' ';
}

signed main()
{
	ios::sync_with_stdio(0);
	cin.tie(0), cout.tie(0);

	int t = 1; //cin >> t;
	while (t--) solve();

	return 0;
}

感谢观看。