Leetcode 1240：铺瓷砖（超详细的解法！！！）

你是一位施工队的工长，根据设计师的要求准备为一套设计风格独特的房子进行室内装修。

房子的客厅大小为 n x m，为保持极简的风格，需要使用尽可能少的 正方形 瓷砖来铺盖地面。

假设正方形瓷砖的规格不限，边长都是整数。

请你帮设计师计算一下，最少需要用到多少块方形瓷砖？

示例 1：

输入：n = 2, m = 3
输出：3
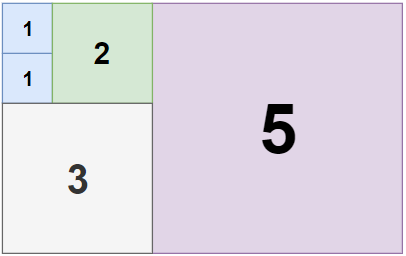
解释：3 块地砖就可以铺满卧室。
     2 块 1x1 地砖
     1 块 2x2 地砖

示例 2：

输入：n = 5, m = 8
输出：5

示例 3：

输入：n = 11, m = 13
输出：6

提示：

• 1 <= n <= 13
• 1 <= m <= 13

解题思路

这是一个经典的问题，该问题源自这篇论文Tiling a rectangle with the fewest squares。当然我们这里肯定不会这么复杂的去做，这里给出两种解法。

首先考虑dfs的解法，也就是一行一行的去枚举可以放的矩形，例如：

此时我们将第一行的所有矩形都确定了，接着考虑第二行的矩形，那么这里应该是从绿色（第2个）下面开始放，然后再放紫色的（第4个），也就是从最低高度开始放。当所有矩形的高度都是大矩形的高度n时，那么此时摆放成功，记录结果。为了记录每个矩形的高度，我们需要开辟m大小的数组（记录每个位置的高度）。对于第一个例子，最后记录（最后一层）的就是[1,2,2]。需要注意的是，我们实际放正方形的时候采用贪心策略（从最大的开始放），所以并不会出现上图中的情形。

最后代码非常简洁：

class Solution:
    def tilingRectangle(self, n: int, m: int) -> int:
        res = m * n    
        def dfs(ht, moves):
            if all(h == n for h in ht):
                res = min(res, moves)
                return
            if moves >= res