Leetcode 279:完全平方数（最详细解决方案！！！）

给定正整数 n，找到若干个完全平方数（比如 1, 4, 9, 16, ...）使得它们的和等于 n。你需要让组成和的完全平方数的个数最少。

示例 1:

输入: n = 12
输出: 3 
解释: 12 = 4 + 4 + 4.

示例 2:

输入: n = 13
输出: 2
解释: 13 = 4 + 9.

解题思路

很多人第一眼看到这个问题，想到的第一种做法就是使用贪心算法，但是对于这个问题是不适用的，例如：

12 = 9 + 1 + 1 + 1

我们根据题目中完全平方数的个数最少，我们在什么算法中用到过最少这个关键字？啊哈！最短路径问题。那么和这个问题有什么联系呢？

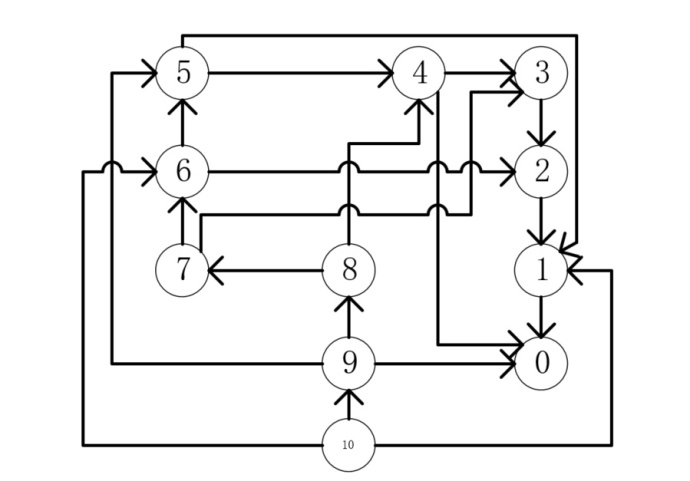
现在我们就可以用最短路径算法来解决这个问题。最短路径算法其实就是图的广度优先遍历。例如对于上图中的5，我们要前往0，我们的第一步有两种走法，先走4和先走1。所以我们需要建立一个队列或者栈，然后将第一步的走法压入队列或者栈中。如下（使用队列， 我们同时记录走的步数）

q : (4, 1) (1, 1)

我们将4出队，然后看4的下一步怎么走，发现只能走3，所以我们将(3, 2)入队

q : (1, 1) (3, 2)

接着我们将(1, 1)弹出，我们看1的下一步怎么走，发现只能走0，这个时候我们发现已经到达了0，那么我们更新step+1，然后出循环即可。以下是代码的全部过程：

class Solution:
    def numSquares(self, n):
        """
        :type n: int
        :rtype: int
        """
        q = list()
        q.append([n, 0])
        visited = [False for _ in range(n+1)]
        visited[n] = True

        while any(q):
            num, step = q.pop(0)

            i = 1
            tNum = num - i**2
            while tNum >&