Leetcode 42：接雨水（超详细的解法！！！）

给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

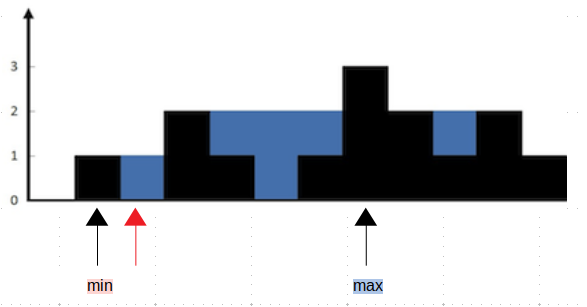
上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图，在这种情况下，可以接 6 个单位的雨水（蓝色部分表示雨水）。 感谢 Marcos 贡献此图。

示例:

输入: [0,1,0,2,1,0,1,3,2,1,2,1]
输出: 6

解题思路

我们首先想到的做法就是木桶原理，我们只要找到给定区间的左边界和右边界的最小值，那么这个区间内的盛水量就是最小边界减去中间的height。现在我们的问题就变成了，怎么去找这样的区间？我们遍历i=[1:len(height)-2]，然后分别在i的左右找最大边界即可。

class Solution:
    def trap(self, height):
        """
        :type height: List[int]
        :rtype: int
        """
        res, hei_len = 0, len(height)
        for i in range(1, hei_len-1):
            max_left, max_right = 0, 0
            for l in range(i+1):
                max_left = max(max_left, height[l])
            for r in range(i, hei_len):
                max_right = max(max_right, height[r])
                
            res += min(max_left, max_right) - height[i]
            
        return res

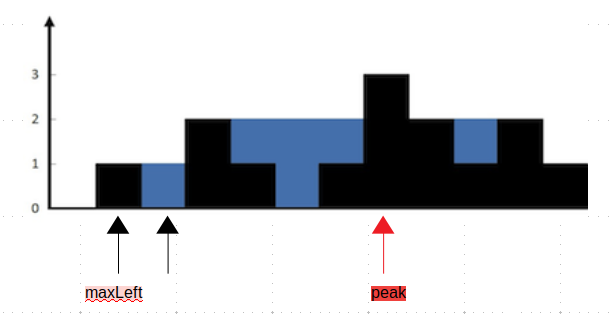
我们将这个代码提交到leetcode果然超时了。其实我在拿到这个问题的时候想到的是，这就是一个爬山问题。我们可以先找到山峰的位置，这样山峰左侧一定是上升趋势，而山峰右侧一定是下降趋势。那么我们在山峰左侧的时候，从左向山峰走，这样我们一定可以知道当前的左侧的最大值，并且知道当前的最低水位。我们在山峰右侧的时候，从右向山峰走，这样我们一定可以知道当前的右侧的最大值，并且知道当前的最低水位。

class Solution:
    def trap(self, height):
        """
        :type height: List[int]
        :rtype: int
        """
        res, hei_len, peak = 0, len(height), 0
        if hei_len < 3:
            return 0
        max_val = height[0]
        for i in range(1, hei_len):
            if height[i] >= max_val:
                max_val = height[i]
                peak = i
        
        max_left, max_right = height[0], height[-1]
        for i in range(peak):
            if max_left < height[i]:
                max_left = height[i]
            else:
                res += max_left - height[i]
                
        for i in range(hei_len-1, peak, -1):
            if max_right < height[i]:
                max_right = height[i]
            else:
                res += max_right - height[i]
            
        return res

还有一种比较不错的处理思路，采用对撞指针的方法。

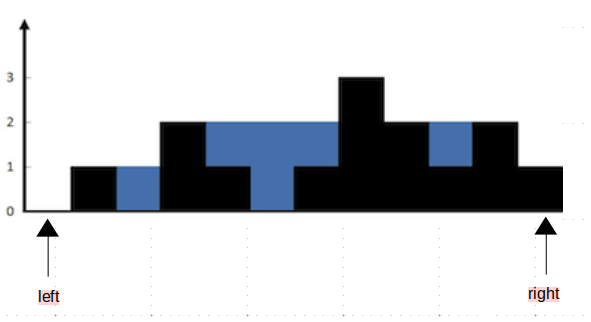
我们首先建立left和right两个指针。我们首先判断height[left]<height[right]，如果成立的话，我们left+=1，否则的话，我们right-=1。

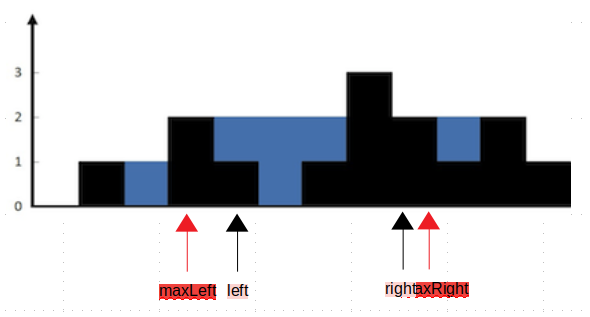
我们挪动left和right的同时需要记录左右的最大值maxLeft和maxRight。如果height[left]<height[right]并且height[left]<maxLeft的话，那么说明此时的left处于较低位置，我们应该增加水量。但是增加多少呢？maxLeft-height[left]还是height[right]-height[left]呢？很明显是前者，通过反证法很好得到这个结论。如果height[left]>=height[right]并且height[right]<maxRight的话，那么说明此时的right处于较低位置，我们应该增加maxRight-height[right]水量。

class Solution:
    def trap(self, height):
        """
        :type height: List[int]
        :rtype: int
        """
        left, right = 0, len(height) - 1
        left_max, right_max = 0, 0
        res = 0
        while left < right:
            if height[left] < height[right]:
                if height[left] >= left_max:
                    left_max = height[left]
                else:
                    res += left_max - height[left]
                left += 1
            else:
                if height[right] >= right_max:
                    right_max = height[right]
                else:
                    res += right_max - height[right]
                right -= 1
                
        return res

这个问题还有一个不错的解法就是使用单调栈Leetcode 单调栈问题总结（超详细！！！），我们可以建立一个单调递减的栈，此时我们关注的问题就是如果出现一个元素比栈顶元素大的话，那么此时必然可以形成凹槽，此时我们只需要计算凹槽长度和边界的高度差那么必然可以计算出接水的面积。

class Solution:
    def trap(self, height):
        len_h = len(height)
        if len_h < 3:
            return 0
        
        stack, res = list(), 0
        for i in range(len_h):
            while stack and height[stack[-1]] < height[i]:
                tmp = stack.pop()
                if stack:
                    res += (min(height[i], height[stack[-1]]) - \
                            height[tmp])*(i - stack[-1] - 1)
            stack.append(i)
        return res

reference:

https://leetcode.com/problems/trapping-rain-water/solution/

我将该问题的其他语言版本添加到了我的GitHub Leetcode

如有问题，希望大家指出！！！