Leetcode 134： 加油站（超详细的解法！！！）

在一条环路上有 N 个加油站，其中第 i 个加油站有汽油 gas[i] 升。

你有一辆油箱容量无限的的汽车，从第 i 个加油站开往第 i+1 个加油站需要消耗汽油 cost[i] 升。你从其中的一个加油站出发，开始时油箱为空。

如果你可以绕环路行驶一周，则返回出发时加油站的编号，否则返回 -1。

说明:

• 如果题目有解，该答案即为唯一答案。
• 输入数组均为非空数组，且长度相同。
• 输入数组中的元素均为非负数。

示例 1:

输入: 
gas  = [1,2,3,4,5]
cost = [3,4,5,1,2]

输出: 3

解释:
从 3 号加油站(索引为 3 处)出发，可获得 4 升汽油。此时油箱有 = 0 + 4 = 4 升汽油
开往 4 号加油站，此时油箱有 4 - 1 + 5 = 8 升汽油
开往 0 号加油站，此时油箱有 8 - 2 + 1 = 7 升汽油
开往 1 号加油站，此时油箱有 7 - 3 + 2 = 6 升汽油
开往 2 号加油站，此时油箱有 6 - 4 + 3 = 5 升汽油
开往 3 号加油站，你需要消耗 5 升汽油，正好足够你返回到 3 号加油站。
因此，3 可为起始索引。

示例 2:

输入: 
gas  = [2,3,4]
cost = [3,4,3]

输出: -1

解释:
你不能从 0 号或 1 号加油站出发，因为没有足够的汽油可以让你行驶到下一个加油站。
我们从 2 号加油站出发，可以获得 4 升汽油。 此时油箱有 = 0 + 4 = 4 升汽油
开往 0 号加油站，此时油箱有 4 - 3 + 2 = 3 升汽油
开往 1 号加油站，此时油箱有 3 - 3 + 3 = 3 升汽油
你无法返回 2 号加油站，因为返程需要消耗 4 升汽油，但是你的油箱只有 3 升汽油。
因此，无论怎样，你都不可能绕环路行驶一周。

解题思路

这个问题非常有意思，首先我们可以很快的判定出是否存在答案。我们只需要将所有的gas - cost累加，如果结果小于0，自然就不会存在解了。现在我们的问题就变成了如何判定起始位置。首先我们知道我们的起始点一定gas - cost>0，并且我们在gas-cost累加的过程中不能出现负数。对于第一点很好理解，因为如果小于零的话，我们就无法出发。对于第二点，如果中途出现负数的话，那么就表示我们无法到达最后一个将和变成负数的点的位置。这个累加的过程让我联想起了波形的变化

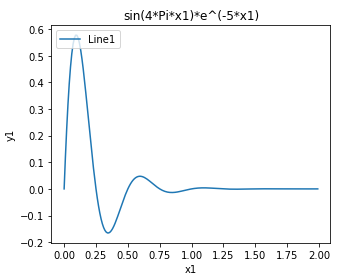
此时我们将波形联系成gas-cost不断累加的结果，这个结果有正有负。

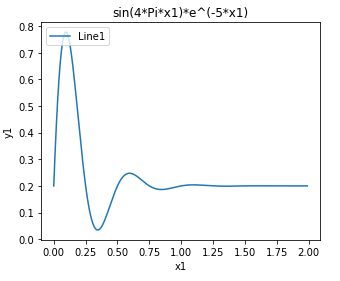
我们需要我们的波形不出现负数，那么只需要将整个波形向上平移即可。那么我们需要向上平移多少呢？我们只需要知道整个波形的最小值即可。那么我们最后的问题的就变成了求累加过程的最小值，我们从最小值的下一个位置出发即可（为什么是下一个位置？因为当前最小值的位置必然gas-cost<0）。

class Solution:
    def canCompleteCircuit(self, gas, cost):
        """
        :type gas: List[int]
        :type cost: List[int]
        :rtype: int
        """
        res = -1
        all_sum, min_sum = 0, float('inf')
        n = len(gas)
        for i in range(n):
            all_sum += gas[i] - cost[i]
            if min_sum > all_sum:
                min_sum = all_sum
                res = (i + 1)%n
                
        if all_sum < 0:
            return -1
        
        return res

我将该问题的其他语言版本添加到了我的GitHub Leetcode

如有问题，希望大家指出！！！