一.引入
对于Adaboost,可以说是久闻大名,据说在Deep Learning出来之前,SVM和Adaboost是效果最好的 两个算法,而Adaboost是提升树(boosting tree),所谓“提升树”就是把“弱学习算法”提升(boost)为“强学习算法”(语自《统计学习方法》),而其中最具代表性的也就是Adaboost了,貌似Adaboost的结构还和Neural Network有几分神似,我倒没有深究过,不知道是不是有什么干货
二.过程
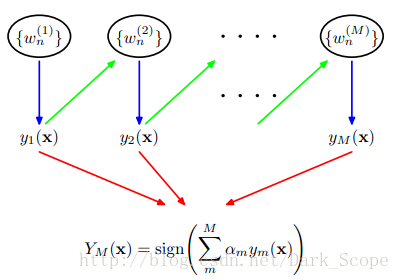
这就是Adaboost的结构,最后的分类器YM是由数个弱分类器(weak classifier)组合而成的,相当于最后m个弱分类器来投票决定分类,而且每个弱分类器的“话语权”α不一样。
这里阐述下算法的具体过程:
1.初始化所有训练样例的权重为1 / N,其中N是样例数
2.for m=1,……M:
a).训练弱分类器ym(),使其最小化权重误差函数(weighted error function):
b)接下来计算该弱分类器的话语权α:
c)更新权重:
其中Zm:
是规范化因子,使所有w的和为1。(这里公式稍微有点乱)
3.得到最后的分类器:
三.原理
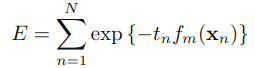
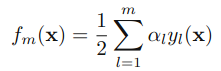
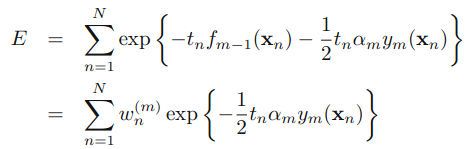
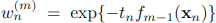 ,可以被看做一个常量,因为它里面没有αm和ym:
,可以被看做一个常量,因为它里面没有αm和ym:
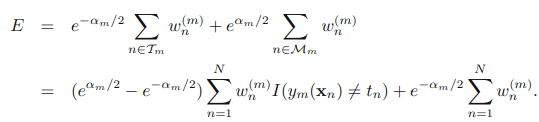
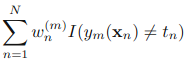
四.实现
 )
)
- # coding: UTF-8
- from __future__ import division
- import numpy as np
- import scipy as sp
- from weakclassify import WEAKC
- from dml.tool import sign
- class ADABC:
- def __init__(self,X,y,Weaker=WEAKC):
- '''''
- Weaker is a class of weak classifier
- It should have a train(self.W) method pass the weight parameter to train
- pred(test_set) method which return y formed by 1 or -1
- see detail in <统计学习方法>
- '''
- self.X=np.array(X)
- self.y=np.array(y)
- self.Weaker=Weaker
- self.sums=np.zeros(self.y.shape)
- self.W=np.ones((self.X.shape[1],1)).flatten(1)/self.X.shape[1]
- self.Q=0
- #print self.W
- def train(self,M=4):
- '''''
- M is the maximal Weaker classification
- '''
- self.G={}
- self.alpha={}
- for i in range(M):
- self.G.setdefault(i)
- self.alpha.setdefault(i)
- for i in range(M):
- self.G[i]=self.Weaker(self.X,self.y)
- e=self.G[i].train(self.W)
- #print self.G[i].t_val,self.G[i].t_b,e
- self.alpha[i]=1/2*np.log((1-e)/e)
- #print self.alpha[i]
- sg=self.G[i].pred(self.X)
- Z=self.W*np.exp(-self.alpha[i]*self.y*sg.transpose())
- self.W=(Z/Z.sum()).flatten(1)
- self.Q=i
- #print self.finalclassifer(i),'==========='
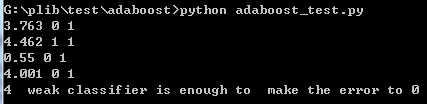
- if self.finalclassifer(i)==0:
- print i+1," weak classifier is enough to make the error to 0"
- break
- def finalclassifer(self,t):
- '''''
- the 1 to t weak classifer come together
- '''
- self.sums=self.sums+self.G[t].pred(self.X).flatten(1)*self.alpha[t]
- #print self.sums
- pre_y=sign(self.sums)
- #sums=np.zeros(self.y.shape)
- #for i in range(t+1):
- # sums=sums+self.G[i].pred(self.X).flatten(1)*self.alpha[i]
- # print sums
- #pre_y=sign(sums)
- t=(pre_y!=self.y).sum()
- return t
- def pred(self,test_set):
- sums=np.zeros(self.y.shape)
- for i in range(self.Q+1):
- sums=sums+self.G[i].pred(self.X).flatten(1)*self.alpha[i]
- #print sums
- pre_y=sign(sums)
- return pre_y


 )
)








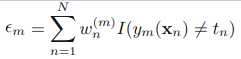
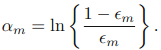
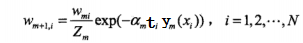
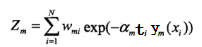
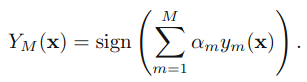














 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








