五、【串匹配】KMP算法详解

最新推荐文章于 2022-05-17 20:01:13 发布

csu_zhengzy~

最新推荐文章于 2022-05-17 20:01:13 发布

阅读量593

点赞数 3

分类专栏：算法文章标签：串匹配 KMP算法

本文链接：https://blog.csdn.net/qq_18108083/article/details/85249999

版权

算法专栏收录该内容

14 篇文章 0 订阅

订阅专栏

串或者字符串属于线性结构，可以使用向量和列表等很方便地实现，其也具有很鲜明的特征：结构简单、规模庞大、元素重复率高。在涉及字符串的众多应用中，字符串匹配是最常使用也是最为重要的操作。

字符串匹配算法大约有30多种，本文介绍最为著名的KMP算法，KMP算法的性能与常规的蛮力算法相比有巨大的性能提升，但由于其巧妙的算法思路和实现技巧，我在理解KMP算法上花费了好大的功夫，言归正传，下面进行详细介绍。

问题描述

给一个文本串S，和一个模式串P，现在要查找文本串S是否包含模式串P，如果包含，返回包含的起始位置。

如文本串S“BBC ABCDAB ABCDABCDABDE”，和模式串P“ABCDABD”，现在要拿模式串P去跟文本串S匹配。

一、蛮力算法

如果用蛮力匹配的思路，并假设现在文本串S匹配到 i 位置，模式串P匹配到 j 位置，则有：

(a) 如果当前字符匹配成功（即S[i] == P[j]），则i++，j++，继续匹配下一个字符；

(b) 如果失配（即S[i] ! = P[j]），令i = i - (j - 1)，j = 0。相当于每次匹配失败时，i 回溯，j 被置为0。

int match ( char* P, char* T ) //串匹配算法
{ 
    size_t n = strlen ( T ), i = 0; //文本串长度、当前接受比对字符的位置
    size_t m = strlen ( P ), j = 0; //模式串长度、当前接受比对字符的位置
    while ( j < m && i < n ) //自左向右逐个比对字符
       if ( T[i] == P[j] ) //若匹配
          { i ++;  j ++; } //则转到下一对字符
       else //否则
          { i -= j - 1; j = 0; } //文本串回退、模式串复位
    return i - j; //返回位置
 }

过程如下：

1.S[0]为B，P[0]为A，不匹配，执行第b条指令：“如果失配（即S[i]! = P[j]），令i = i - (j - 1)，j = 0”，S[1]跟P[0]匹配，相当于模式串要往右移动一位（i=1，j=0）

2. S[1]跟P[0]还是不匹配，继续执行第b条指令：“如果失配（即S[i]! = P[j]），令i = i - (j - 1)，j = 0”，S[2]跟P[0]匹配（i=2，j=0），从而模式串不断的向右移动一位（不断的执行“令i = i - (j - 1)，j = 0”，i从2变到4，j一直为0）

3. 直到S[4]跟P[0]匹配成功（i=4，j=0），此时按照上面的暴力匹配算法的思路，转而执行第a条指令：“如果当前字符匹配成功（即S[i] == P[j]），则i++，j++”，可得S[i]为S[5]，P[j]为P[1]，即接下来S[5]跟P[1]匹配（i=5，j=1）

4. S[5]跟P[1]匹配成功，继续执行第a条指令：“如果当前字符匹配成功（即S[i] == P[j]），则i++，j++”，得到S[6]跟P[2]匹配（i=6，j=2），如此进行下去

5. 直到S[10]为空格字符，P[6]为字符D（i=10，j=6），因为不匹配，重新执行第b条指令：“如果失配（即S[i]! = P[j]），令i = i - (j - 1)，j = 0”，相当于S[5]跟P[0]匹配（i=5，j=0）

6. 至此，我们可以看到，如果按照暴力匹配算法的思路，尽管之前文本串和模式串已经分别匹配到了S[9]、P[5]，但因为S[10]跟P[6]不匹配，所以文本串回溯到S[5]，模式串回溯到P[0]，从而让S[5]跟P[0]匹配。

而S[5]肯定跟P[0]失配。为什么呢？因为在之前第4步匹配中，我们已经得知S[5] = P[1] = B，而P[0] = A，即P[1] != P[0]，故S[5]必定不等于P[0]，所以回溯过去必然会导致失配，所以可见蛮力算法进行了很多无用的比较。

性能：对于长度为n的文本串及长度为m的模式串，蛮力算法至多迭代n-m+1次，且各轮至多需要比对m次。因为m<<n，所以蛮力算法的的时间复杂度为O(m*n)。

那有没有一种算法，让i 不往回退，只需要移动j 即可呢？事实上，KMP算法可以做到，它利用之前在之前匹配中的记忆，保持 i 不回溯，通过修改j 的位置，让模式串尽量地移动到有效的位置。

二、KMP算法

Knuth-Morris-Pratt 字符串查找算法，简称为 “KMP算法”，常用于在一个文本串S内查找一个模式串P 的出现位置，这个算法由Donald Knuth、Vaughan Pratt、James H. Morris三人于1977年联合发表，故取这3人的姓氏命名此算法。

KMP的算法流程：

(a) 如果j = -1，或者当前字符匹配成功（即S[i] == P[j]），都令i++，j++，继续匹配下一个字符；

(b) 如果j != -1，且当前字符匹配失败（即S[i] != P[j]），则令 i 不变，j = next[j]。此举意味着失配时，模式串P相对于文本串S向右移动了j - next [j] 位,，且此值大于等于1。

next 数组各值的含义：代表模式串中，在当前字符之前的字符串，有多大长度的相同真前缀后缀。例如如果next [j] = k，代表 j 之前的字符串中有最大长度为k 的相同真前缀后缀。

此也意味着在某个字符失配时，该字符对应的next 值会告诉你下一步匹配中，模式串应该跳到哪个位置（跳到next [j] 的位置）。如果next [j] 等于0或-1，则跳到模式串的开头字符，若next [j] = k 且 k > 0，代表下次匹配跳到j 之前的某个字符，而不是跳到开头。

int match(char* P, char* T)
{
	int* next = buildNext(P);   //构造next表
	int n = (int)strlen(T), i = 0;  //文本串指针
	int m = (int)strlen(P), j = 0;  //模式串指针
	while (j < m&&i < n)   //自左向右逐个比对字符
	{
		if (0 > j || T[i] == P[j])   //若匹配
		{
			i++;   //转移到下一字符
			j++;
		}
		else  //若不匹配
			j = next[j];  //模式串右移(查询next表)
	}
	delete[] next;  //释放表
	return i - j;   //返回匹配位置
}

继续拿之前的例子来说，当S[10]跟P[6]匹配失败时，KMP不是跟暴力匹配那样简单的把模式串右移一位，而是执行第b条指令：“如果j != -1，且当前字符匹配失败（即S[i] != P[j]），则令 i 不变，j = next[j]”，即 j 从6变到2（后面我们将求得P[6]，即字符D对应的next 值为2），所以相当于模式串向右移动的位数为j - next[j]（j - next[j] = 6-2 = 4），由此省略了很多无用的比较。

向右移动4位后，S[10]跟P[2]继续匹配。为什么要向右移动4位呢，因为移动4位后，模式串中又有个“AB”可以继续跟S[8]S[9]对应着，从而不用让 i 回溯。相当于在除去字符D的模式串子串中寻找相同的真前缀和后缀，然后根据前缀后缀求出next 数组，最后基于next 数组进行匹配。

next实现正确跳转的内部原理：

匹配失配时，j = next [j]，模式串向右移动的位数为：j - next[j]。换言之，当模式串的后缀pj-k pj-k+1, ..., pj-1 跟文本串si-k si-k+1, ..., si-1匹配成功，但pj 跟si匹配失败时，因为next[j] = k，相当于在不包含pj的模式串中有最大长度为k 的相同真前缀后缀，即p[0] p[1] ...p[k-1] = p[j-k] p[j-k+1]...p[j-1]，故令j = next[j]，从而让模式串右移j - next[j] 位，使得模式串的前缀p[0] p[1], ..., p[k-1]对应着文本串 s[i-k] s[i-k+1], ..., s[i-1]，而后让p[k]跟s[i] 继续匹配。如下图所示：

所以说，KMP算法的精髓就在于可以直接利用next数组进行跳转，使文本串i不必回溯，使模式串尽可能地右移，从而避免了大量无用的比较，提升了算法的性能。

next数组的求法

计算next 数组的方法可以采用递推进行计算，其过程实质就是模式串的自匹配过程：对于模式串中的每个字符p[j]，分别检查在这个字符之前的子串中是否存在长度为k的真前缀和真后缀相等，取满足这种情况的最大值k，则记next[j]=k。其中具有一个特例，即当j=0时，要求next[j]=-1，这是使当匹配时文本串S和模式串P的在i=j=0时就发生不匹配的时候，文本串需要向右移一位。

基于之前的理解，可知：

next[0] = -1；

下面开始根据next[j]求解next[j+1] ，对于P的前 j+1个序列字符，有（下面为重点，细细理解是能懂的）

(a) 若p[k] == p[j]，则next[j + 1 ] = next [j] + 1 = k + 1；（这里考察的是p[j+1]之前的子串<求第j+1的对应的next值就只会考虑在其之前的子串的匹配情况，而无需考虑自身的匹配情况>，事实上k=next[j]，k为在j之前的子串中满足真前缀和真后缀相对的最大前缀及后缀长度）

(b) 若p[k ] ≠ p[j]，则j像上述的文本串指针i一样也不会回溯，转而调整模式串的子串指针，要逐渐试探更短的前缀以匹配后缀（这样取next[k]只能保证P[0]~P[next[k]-1]==P[j-next[k]~P[j-1]匹配成功，而P[j]仍然是不能保证的，只能不断试探，若某一次真的使p[ next[k] ] == p[j ]，则表示试探成功，成功地确定了next[j+1]，否则依然需要继续往下试探，逐渐缩短前缀的长度继续试探）。----如果此时p[ next[k] ] == p[j ]，则next[ j + 1 ] = next[k] + 1，否则继续递归前缀索引k = next[k]，而后重复此过程。相当于在字符p[j+1]之前不存在长度为k+1的前缀"p[0] p[1], …, p[k-1] p[k]"跟后缀“p[j-k] p[j-k+1], …, p[j-1] p[j]"相等，那么是否可能存在另一个值t+1 < k+1，使得长度更小的前缀 “p[0] p[1], …, p[t-1] p[t]” 等于长度更小的后缀 “p[j-t] p[j-t+1], …, p[j-1] p[j]” 呢？如果存在，那么这个t+1 便是next[ j+1]的值，此相当于利用已经求得的next 数组（next [0, ..., k, ..., j]）进行P串前缀跟P串后缀的匹配。

再从图形解释为何递归前缀索引k = next[k]，就能找到长度更短的相同前缀后缀呢，这归根到next数组的含义。我们拿前缀 p0 pk-1 pk 去跟后缀pj-k pj-1 pj匹配，如果pk 跟pj 失配，下一步就是用p[next[k]] 去跟pj 继续匹配，如果p[ next[k] ]跟pj还是不匹配，则需要寻找长度更短的相同前缀后缀，即下一步用p[ next[ next[k] ] ]去跟pj匹配。此过程相当于模式串的自我匹配，所以不断的递归k = next[k]，直到要么找到长度更短的相同前缀后缀，要么没有长度更短的相同前缀后缀。如下图所示：

开始时P[k]不行，P[k]！=P[j]，转而试探更短的前缀P[0]-P[next[k]]，结果试探成功P[k]==P[j]（刚好这一次比较幸运，否则还需要继续试探next[next[k]]。为什么每次都选择K=next[k]进行试探呢？因为next[k]数组都是之前生成好的，能确保P[0]~P[next[k]-1]==P[j-next[k]~P[j-1]，只可能试探前缀的下一个字符不一定等于Pj，这也是试探的目的）

由上可得next数组的构造代码，如下

int* buildNext(char* p)
{
	size_t m = strlen(p);
	size_t j = 0;
	int* N = new int[m];  //next表
	int t = N[0] = -1;    //通配符
	while (j < m - 1)
	{
		if (0 > t || p[j] == p[t])
		{
			j++;
			t++;
			N[j] = t;  //成功则填写next数组
		}
		else
			t = N[t];  //试探更短的前缀
	}
	return N;
}

求得上例中模式串的next数组
字符	A	B	A	C	A	B	D
next值	-1	0	0	0	0	1	2

基于next数组进行匹配：

还是给定文本串“BBC ABCDAB ABCDABCDABDE”，和模式串“ABCDABD”，现在要拿模式串去跟文本串匹配：

1. 最开始匹配时P[0]跟S[0]匹配失败，所以执行“如果j != -1，且当前字符匹配失败（即S[i] != P[j]），则令 i 不变，j = next[j]”，所以j = -1，故转而执行“如果j = -1，或者当前字符匹配成功（即S[i] == P[j]），都令i++，j++”，得到i = 1，j = 0，即P[0]继续跟S[1]匹配，再次失败，知道P[0]与S[4]进行匹配成功，开始执行此条指令的后半段：“如果j = -1，或者当前字符匹配成功（即S[i] == P[j]），都令i++，j++”。

2. P[1]跟S[5]匹配成功，P[2]跟S[6]也匹配成功, ...，直到当匹配到P[6]处的字符D时失配（即S[10] != P[6]），由于P[6]处的D对应的next 值为2，所以下一步用P[2]处的字符C继续跟S[10]匹配，相当于向右移动：j - next[j] = 6 - 2 =4 位。

3. 向右移动4位后，P[2]处的C再次失配，由于C对应的next值为0，所以下一步用P[0]处的字符继续跟S[10]匹配，相当于向右移动：j - next[j] = 2 - 0 = 2 位。

4. 移动两位之后，A 跟空格不匹配，next[0]=-1，模式串后移1 位。

5.P[6]处的D再次失配，因为P[6]对应的next值为2，故下一步用P[2]继续跟文本串匹配，相当于模式串向右移动 j - next[j] = 6 - 2 = 4 位。

6. 匹配成功，过程结束。

可见基于next数组的KMP算法能和蛮力算法取得同样正确的效果，但是在KMP算法进行的过程中，智能地跳过了很多注定错误的比较，正是凭借着这种智能，KMP算法才具有很高的匹配效率，尽管按照next数组跳，依然还是会发送匹配的错误（这个在下面可以得到优化）。

性能分析：此时算法的时间复杂度不方便直接看出来，清华大学的《数据结构》(邓俊辉)中通过直接分析代码，巧妙地通过分析K=2i-j是单调递增（无论是否进入else），而且上限为2*n，证明KMP算法(不包含next构造过程)的时间复杂度为O(n)，加上next数组构造花费的O(m)（其代码框架等同于KMP算法），其总共的时间复杂度为O(n+m)。

next数组的优化

通过上面的过程，我们发现即使使用next表进行跳转能避免很多注定失败的匹配，但是仍然会存在一些失败的匹配，事实上，经过分析，我们其实是能进一步消除一些注定失败的匹配的。

分析：从上面对next表的功能的介绍可以知道，当S[i]！=P[j]时，令j=next[j]，实质上可以保证P[0]~P[next[j]-1]==S[i-next[j]]~S[i-1]，从而可以略过很多必定失败的匹配（若连上面的等式都不能满足，则必定失败），而对于S[i]是否等于P[next[j]]是不知道的，这也是需要进行i=next[next[i]]迭代来缩短前缀子串进行试探的原因，但是事实上还有一个已知的条件没有用到：若P[j]==P[next[j]]，则这种情况也必定失败！因为之前P[j]！=S[i]是已知的，之前已经拿P[j]这个鸡蛋碰S[j]这个石头，P[j]这个鸡蛋破了之后，依然拿P[next[j]]这个和P[j]一样的也是鸡蛋的东西碰S[j]，肯定也注定失败，所以优化的目的就是避免这种情况的匹配----在next表的构造过程中进行优化。

需要规避的情况的举例：

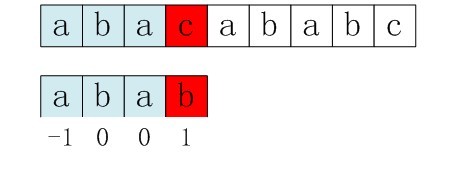
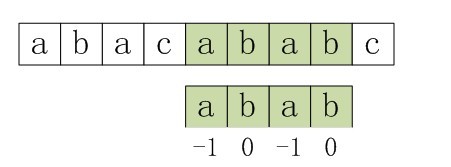
比如，如果用之前的next 数组方法求模式串“abab”的next 数组，可得其next 数组为-1 0 0 1（0 0 1 2整体右移一位，初值赋为-1），当它跟下图中的文本串去匹配的时候，发现b跟c失配，于是模式串右移j - next[j] = 3 - 1 =2位。

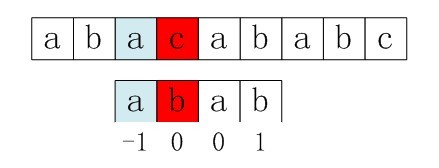
右移2位后，b又跟c失配。事实上，因为在上一步的匹配中，已经得知p[3] = b，与s[3] = c失配，而右移两位之后，让p[ next[3] ] = p[1] = b 再跟s[3]匹配时，必然失配。

优化方案：当p[j] != s[i] 时，下次匹配必然是p[ next [j]] 跟s[i]匹配，如果p[j] = p[ next[j] ]，必然导致后一步匹配失败，所以不能允许p[j] = p[ next[j ]]。如果出现了p[j] = p[ next[j] ]咋办呢？如果出现了，则需要再次递归，即令next[j] = next[ next[j] ]，就是直接跳过，换下一个更短的前缀进行试探！

优化后的代码如下

int* buildNext(char* P) //构造模式串P的next表（改进版本）
{ 
	    size_t m = strlen(P), j = 0; //“主”串指针
	    int* N = new int[m]; //next表
	    int t = N[0] = -1; //模式串指针
	    while (j < m - 1)
		       if (0 > t || P[j] == P[t]) 
			   { //匹配
		          N[j] = (P[++j] != P[++t] ? t : N[t]); //注意此句与未改进之前的区别
				}
		else //失配
			   t = N[t];
	    return N;
}

使用优化后的next表举例：

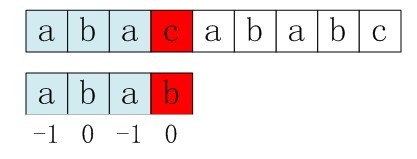
1. S[3]与P[3]匹配失败。

2. S[3]保持不变，P的下一个匹配位置是P[next[3]]，而next[3]=0，所以P[next[3]]=P[0]与S[3]匹配（注意此时不会像之前那样进行S[2]和P[0]的比较）。

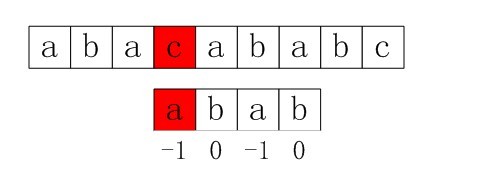
3. 由于上一步骤中P[0]与S[3]还是不匹配。此时i=3，j=next [0]=-1，由于满足条件j==-1，所以执行“++i, ++j”，即主串指针下移一个位置，P[0]与S[4]开始匹配。最后j==pLen，跳出循环，输出结果i - j = 4（即模式串第一次在文本串中出现的位置），匹配成功，算法结束。

1. 本文中的例子来自 https://blog.csdn.net/v_july_v/article/details/7041827

2. 教材：《数据结构(c++语言版)》（清华大学）

csu_zhengzy~

关注

3
点赞
踩
1

收藏

觉得还不错? 一键收藏
0
评论
五、【串匹配】KMP算法详解

串或者字符串属于线性结构，可以使用向量和列表等很方便地实现，其也具有很鲜明的特征：结构简单、规模庞大、元素重复率高。在涉及字符串的众多应用中，字符串匹配是最常使用也是最为重要的操作。字符串匹配算法大约有30多种，本文介绍最为著名的KMP算法，KMP算法的性能与常规的蛮力算法相比有巨大的性能提升，但由于其巧妙的算法思路和实现技巧，我在理解KMP算法上花费了好大的功夫，言归正传，下面进行详细介绍。...
复制链接

扫一扫

专栏目录