第七章-递归数据类型

递归数据类型

递归数据类型在编程中的地位举足轻重，而归纳法本质上讨论的都是递归数据类型。

递归数据类型由递归定义指定，即说明如何从之前的数据元素构建新的数据元素。此外,递归数据类型的性质和方法(或函数,function )也同样需要递归定义。最重要的是，基于递归定义，我们可以采用结构归纳法证明给定类型的所有数据都具备某种性质。

7.1 递归定义和结构归纳法

递归数据类型的定义包括两部分:

1. 基本情形指明属于该数据类型的某个已知数学元素。
2. 构造情形指明如何从已知基本元素或已构建的元素，构造新的元素。

给定字符集合A，字符串的定义如下。

**定义 7.1.1：**令非空集合A为字母表，其元素为字符（或字母、符号、数字等,character, letter, symbol, digit )。基于字母表A的递归数据类型$A^{\ast }$定义如下。
**基本情形：**空字符串λ属于$A^{\ast }$
**构造情形：**如果a∈ A且s ∈ $A^{\ast }$，那么<a,s> ∈ $A^{\ast }$

通常,二进制字符串是由0和1组成的序列。例如,我们可以把长度为4的二进制字符串101看成四元组(1,0,1,1)。根据定义7.1.1，这个表达应当是嵌套的元素对，即

用递归的方法定义字符串长度：

**定义7.1.2：**基于定义7.1.1，递归地定义字符串s的长度|s|。

基本情形:|λ|::= 0。
构造情形:|<a,s>|::=1+|s|。

如果要定义一个递归数据类型上的方法f，我们要先定义相应数据类型基本情形的f的值，然后指明在构造情形下，我们如何基于已知的f的值定义新的f的值。

用递归的方法定义字符串的拼接：

**定义7.1.3：**字符串s,t ∈ A*的拼接字符串s ·t的递归定义如下所示

**基本情形：**λ · t : : = t
构造情形：<a, s> · t: := <a , s ·t>

7.1.1 结构归纳法

结构归纳法是对递归定义的数据类型的性质进行证明的方法。和递归定义相同，结构归纳证明也包含两部分:

1. 证明基本情形对应的元素具有某种性质。
2. 证明当构造情形用具有该性质的元素生成新的元素时，新的元素也具有该性质。

例子：

在拼接字符串的例子中，我们从定义可知λ · s :: = s，但是我们不知道s · λ :: = s是否成立，我们可以利用结构归纳法去证明其成立。

**引理7.1.4：*对任意s ∈ A ,s · λ = s。
证明：下面的证明基于拼接的归纳定义7.1.3，采用结构归纳法证明。归纳假设为

因此P(s)为真，完成对构造情形的证明。故基于结构归纳法可知,对任意s ∈ A*,引理7.1.4成立。

综上，归纳法的一般原则如下：

基本情形可以有多个吗???

个人理解：不仅仅是b属于基本情形，后面的r，s也属于基本情形。这里的基本情形是与由r和s组成的构造情形c相对应的，所以认为基本情形只有一种是不对的。

7.2 匹配带括号的字符串

设{]，[}* 为所有由中括号构成的字符串集合，下面这两个字符串便属于集合{]，[}*。

对于字符串s ∈ {],[}*，若其左右括号相互匹配，则称之为匹配字符串。以上两个例子中，左边的字符串不是匹配字符串，右边的是匹配字符串。

匹配字符串也可以按递归数据类型的方式进行定义。

**定义7.2.1：**对匹配字符串集合的递归定义如下所示。

**基本情形：**λ ∈ RecMatch。

**构造情形：**如果 s,t ∈ RecMatch，那么 [ s ] t ∈ RecMatch。

要去证明属于 RecMatch 的字符串的左括号和右括号的数目相等。

首先我们先定义#c(s)，#c(s)表示在字符串s中c ∈ A出现的次数。

由定义7.2.2根据结构归纳法可以推出引理7.2.3：

**引理：**RecMatch中的每个字符串左右括号数均相等。

**证明：**下面的证明采用结构归纳法。归纳假设为

**基本情形：**基于定义7.2.2 可知

故P(λ)为真。

构造情形：基于结构归纳法假设，我们设P(s)和P(t)为真，下面证明P([s]t)为真,

完成对构造情形的证明。故基于结构归纳法可知，对任意字符串s ∈ RecMatch，P(s)恒为真。

警告:当数据类型的递归定义允许通过多种方式构造同一个元素时，我们称这个定义是模糊的( ambiguous )。在 RecMatch 的例子中，我们特地选择了一个非模糊的定义以便更好地递归定义基于RecMatch 的方法。一般来说，在模糊的数据类型定义上是无法递归定义方法的。

**定义7.2.4：**集合AmbRecMatch $\subseteq${]，[}*的递归定义如下。

**基本情形：**λ ∈ AmbRecMatch
**构造情形：**如果s,t ∈ AmbRecMatch，那么[s]和st亦属于AmbRecMatcho

我们定义f(s)表示递归构造字符串s ∈ AmbRecMatch需要进行的操作次数:

这个定义看上去没有问题，但会导致f()有两个值，进而使得:

显然这是不对的。

7.3 非负整数上的递归函数

**定义7.3.1：**非负整数N的递归定义如下。

​ 0∈ N
​ 若n ∈ N，则n后面一个数n＋1 ∈ N。

我们可以从这里发现，定义7.3.1的结构归纳法其实就是一般归纳法，换言之，一般归纳法是结构归纳法的特例。对定义在非负整数上的方法的递归定义也是如此。

7.3.1 N上的一些标准递归函数

例7.3.2阶乘 阶乘一般写成“n!”，这里我们使用符号fac(n)表示阶乘:

fac(0) :: = 1。
当n≥0时，fac (n+1):= (n + 1)- fac (n)。

例7.3.3求和 设S(n)表示 ${\sum }_{i=1}^{n}f(i)$，S(n)的递归定义如下。

s(0):: = 0。
当n≥0时，s(n + 1)::= f(n+ 1)+S(n)。

7.3.2 不规范的函数定义

例子1：

这个“定义”没有基本情形。如果某些f,满足了公式7.2，则任何给f加上一个常数的函数同样满足公式7.2，所以公式7.2没有唯一指明一个函数f。

例子2：

这个“定义”有基本情形,但依旧没有唯一指明一个函数。

例子3：

这个“定义”是矛盾的:它要求f:(6)= 0且f:(6)=1，所以公式7.4定义不了任何事情。

例子4 考拉兹猜想：

该定义有可能没有唯一指明一个函数。

恒为1的常值函数显然是满足公式7.5的，但是否有其他函数也满足就不得而知了。难点在于，f4(n)的第三种情形中参数3n＋1是大于n的，所以就无法用定义在N上的归纳法进行判断。现在已经确定的是任何满足公式7.5的fn在n小于$10^{18}$时取值都是1。

例子5 阿克曼函数：

最后一个例子是阿克曼函数，该函数有两个参数且增长非常之快，它的反函数相应地就增长得极慢，但是却没有上界。这反函数实际上是被用来分析一个有效且高效的算法的—合并寻找算法。最初大家推测该算法的时间复杂度会随着输入的增加呈线性增长，结果发现它实是“线性的”，但需要乘以一个系数，而这个系数基本等于阿克曼函数的反函数。这意味着实用角度而言,确实可以认为合并寻找算法是线性的,毕竟对任何实际中可能存在的输人而言,这个理论上会缓慢增长的系数都不会大于5。

阿克曼函数A可以递归地定义如下：

阿克曼函数之所以特别是因为其把A(m, n)也作为A的参数，而A(m,n)可能远大于m和n。在f2中，我们看到若用参数较大时函数的值去定义参数较小时函数的值，就可能导致递归无法终止。但阿克曼函数不会有这个问题，具体的证明需要一些小技巧(见习题7.25 )。

7.4 算术表达式

表达式求值在任何编程语言中都是很重要的，而通过把表达式当作一种递归数据类型，我们可以更好地了解具体是如何进行表达式求值的。

我们把表达式的数据类型定义为Aexp。具体定义如下：

定义 7.4.1

基本情形:

​ 变量x属于Aexp。

​ 任何非负整数对应的阿拉伯数字k属于Aexp。

构造情形:

若e,f ∈ Aexp，则
[e + f] ∈Aexp，我们称表达式[e + f]为和，e和f是和的项，抑或和项。

​ [e * f] ∈ Aexp，我们称表达式[e * f]为积，e和f是积的项，抑或乘数。

​ -[e] ∈ Aexp，我们称表达式-[e]为负数。

7.4.1 Aexp的替换和求值

求值

给定Aexp e和x的取值n，我们便可以对e求值，即确定eval(e,n)。下面用递归定义说明这个简单、有用的求值过程。

定义7.4.2：

定义在e ∈ Aexp上的求值函数 eval: Aexp x Z→Z的递归定义如下。设n为任意整数。

​ 基本情形：

​ 构造情形：

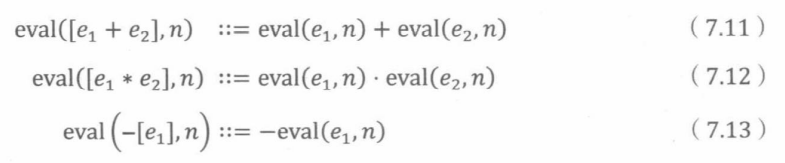
例子：当e为$3+x^2$，n = 2 时

替换

我们用符号subst(f ,e)表示将Aexp e中的所有x替换成f所得的结果。

替换函数的递归定义如下：

**定义7.4.3：**定义在e ∈ Aexp上的替换方法的递归定义如下。设f为任意表达式。

​ 基本情形:

​ 构造情形：

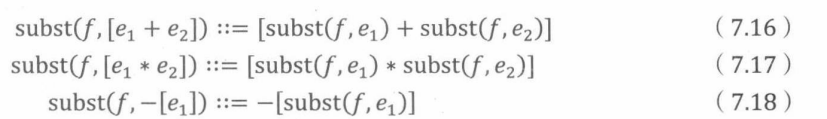
例子：基于上述递归定义将表达式x(x -1)中的x替换成3x:

问题：要求计算x=2时subst(3x,x(x -1))的值

方法一：替换模型

​ 先进行替换得到3x(3x一1)，进而将x =2带入求值，得到30。这种方法可以写成如下表达式

方法二：环境模型

​ 我们先计算出x = 2时3x的值，即6。进而将x = 6带入x(x -1)求值，这种方法可以写成如下表达式

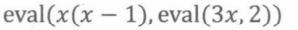
​ 显然替换模型和环境模型总是会产生相同的结果。我们可以基于两种模型的定义直接用结构归纳法对这一结论进行证明。

**定理7.4.4：**对任意表达式e,f ∈ Aexp,n ∈ Z，

**证明：**采用基于e的结构归纳法。

基本情形:
情形[x]
基于替换模型的定义，公式7.21左侧等于eval(f , n);基于求值方法的定义，公式右侧也等于eval( f , n)。
情形[k]
基于替换模型和求值方法的定义，公式7.21左侧等于k;同理，基于求值方法定义可知公式右侧等于k。

构造情形：

情形[e1+ez]
根据结构归纳法假设（参见式7.21)，我们设对于任意f ∈ Aexp,n ∈ Z，

​ 其中i取1或2。我们进而希望证明

​ 基于定义7.4.3中的式7.16，公式7.23左侧等于

​ 再基于定义7.4.2中的式7.11，上式等于

​ 基于归纳假设7.22进一步可知，上式等于

再用定义7.4.2中的式7.11对公式7.23右侧进行变换，最终可知公式7.23成立。

情形[e1*ez]，[-[e1]]证法类似。

7.5 计算机科学中的归纳

归纳法是一种有效且应用广泛的证明方法。强归纳法和一般归纳法都可以用来证明任意定义在非负整数集上的事情，也包括逐步计算过程。

结构归纳法则进一步摆脱了计数的限制，进而为证明递归数据类型和递归计算提供了一种简单有效的方法。

我们也可用归纳法去证明递归数据类型及其性质、方法，但远不如结构归纳法简单直接。

事实上，从理论上来说，结构归纳法比一般归纳法更为强大，但也仅仅是在无限的数据类型上更为有效。所以在实际应用中，结构归纳法的优势主要还在于面对递归数据类型时，这种方法更为简单直接。

23右侧进行变换，最终可知公式7.23成立。

情形[e1*ez]，[-[e1]]证法类似。

7.5 计算机科学中的归纳

归纳法是一种有效且应用广泛的证明方法。强归纳法和一般归纳法都可以用来证明任意定义在非负整数集上的事情，也包括逐步计算过程。

结构归纳法则进一步摆脱了计数的限制，进而为证明递归数据类型和递归计算提供了一种简单有效的方法。

我们也可用归纳法去证明递归数据类型及其性质、方法，但远不如结构归纳法简单直接。

事实上，从理论上来说，结构归纳法比一般归纳法更为强大，但也仅仅是在无限的数据类型上更为有效。所以在实际应用中，结构归纳法的优势主要还在于面对递归数据类型时，这种方法更为简单直接。