第六章:状态机
状态机是对逐步过程的简单抽象。计算机程序可以看作是逐步的计算过程,所以计算机科学领域经常用到状态机。
在计算机科学领域,归纳法最重要的应用之一是证明一个或多个性质在整个过程的各个步骤一直成立。这种在一系列操作或步骤中保持不变的特性,称作保持不变性。
6.1 状态和转移
所谓状态机,其实就是集合上的二元关系,这个集合中的元素称为“状态”,这个关系称为转移关系,转移关系图中的箭头表示一次转移。从状态q到状态r的转移则写作q →r。转移关系又称状态机的状态图。此外,状态机都有一个初始状态。
例子:
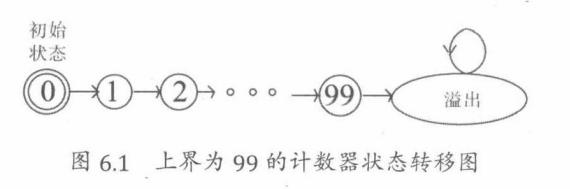
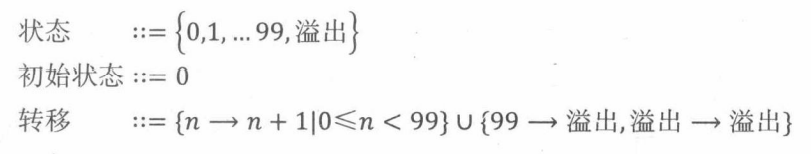
通常,状态机中的状态数目是有限的。但是也存在状态数目是无限的情况,连续计算的状态机往往包含无限个状态。例如,我们可以将以上的例子修改到上界是无穷的,但是此时其状态转移图将很难画出。
6.2 不变性原理
6.2.1 沿对角线移动的机器人
在一个无限的二维整数网格,机器人在这个空间内移动。任意时刻机器人的状态就是它所在位置的二维坐标(x, y)。初始状态为(0,0),机器人每一次移动只能向相邻的对角线网格移动。
求证:机器人能否经过若干次移动到达(1,0)。
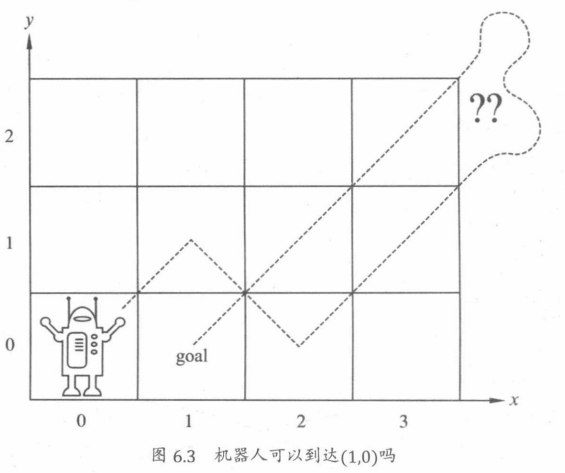
通过观察可知,机器人到达的位置(m,n)都满足m+n为偶数。所以机器人无法到达(1,0)。转移过程中坐标值之和是偶数,这就是保持不变性。
定义状态的偶数和的性质如下:
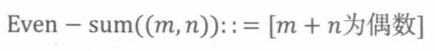
引理6.2.1:给定对角线移动的机器人,对任意转移q→r,如果Even-sum(q),则 Even-sum®
如果q为偶数,且机器人的下一步(-1,-1)(-1,1)(1,-1)(1,1)横纵坐标之和都为偶数,所以r为偶数加偶数,其结果还为偶数。
定理6.2.2:给定沿对角线移动的机器人,它在任何可达状态下的横纵坐标之和都为偶数。
采用归纳法证明,归纳假设为:
P
(
n
)
:
:
=
若机器人在
n
次转移后到达状态
q
,则
E
v
e
n
−
s
u
m
(
q
)
P(n):: = 若机器人在n次转移后到达状态q,则Even - sum(q)
P(n)::=若机器人在n次转移后到达状态q,则Even−sum(q)
**基本步骤:**初始状态为(0,0),0+0是偶数,故P(0)为真。
**归纳步骤:**假设P(n)为真,令r表示任意n+1次转移后的状态。我们现在要证明Even-sum®成立。
设第n次转移后的状态为q,对于转移q–>r,由引理6.2.1可证明成立。所以可以由P(n)成立推出P(n+1)成立。
根据归纳法得出结论,对任意n≥0,若机器人在n次转移后到达状态q,则 Even-sum(q)。所以,该机器人可到达的任何状态都满足 Even-sum性质。
所以,机器人到不了(1,0)。
6.2.2 不变性原理的定义
状态机的执行描述状态机可能采取的步骤构成的序列。
**定义6.2.4:**状态机的执行是指状态机可能具有的状态序列(可能是无限的),满足以下性质
1.从初始状态开始,并且
2.若q, r表示序列中两个连续的状态,那么q →r。
执行中出现的状态是可达的( reachable )。
定义6.2.5:状态机的保持不变性是指关于状态的谓词P满足:对任意状态q,如果P(q)为真,且存在状态r,其中q →r,那么P®也为真。
不变性原理:如果状态机的保持不变性在初始状态为真,则所有可达状态皆为真。
不变性原理与归纳原理:
不变性原理其实是归纳原理在状态机上的重新定义。即:基本步骤是证明初始状态时谓词为真,然后在归纳步骤证明谓词是保持不变式。
6.2.3 示例:虎胆龙威
在电影虎胆龙威中有一个这样的问题,采用3加仑和5加仑的瓶子如何装4加仑的水?
这个装水的问题可以用状态机加以描述:令大壶的装水量为b、小壶的装水量为l,两个子的容量分别是5加仑和3加仑,实数对(b,l)表示状态,其中0≤b≤5、0≤l≤3。(可以证明b,l的可达值是非负整数,注意不能假设未经证明的东西)开始时两个壶都是空的,所以初状态为(0,0)。
该问题的所有状态转移如下:

注意,不同于之前的计数器状态机,这个状态机存在多个状态位置转移。每个状态至多存在一种转移的状态机,称为确定性状态机,比如计数器状态机。如果状态存在多个转移状态,则称为非确定性状态机,比如虎胆龙威状态机。
上述问题解决办法如下:
- 将A装满(3加仑),全部倒入B
- 再次将A装满(3加仑),用A中的水将B装满,此时A有1加仑,B有5加仑
- B中的水全部倒出,将A中的1加仑水倒入B,此时A没有水,B有一加仑
- 再次将A装满(3加仑),将A中的水全部倒入B,此时B中恰有4加仑的水
虎胆龙威终结篇
如果我们将上述壶换为3加仑和9加仑,结果会如何呢?
其状态转移情况与上述相似,除了将5加仑改为9加仑。
对这个状态机而言,任何形如(4,l)的状态都是不可达的。我们用不变性原理对其进行证明。定义保持不变式谓词P((b,l))为b和l都是3的非负倍数。
要证明P对所有虎胆龙威状态机保持不变性,我们假设存在状态q::=(b,l),P(q)为真,并且q→r。接下来要证明P®为真。根据状态转移规则进行分类讨论。
-
是“装满小壶”,即r = (b,3)。由P(q)可知,b是3的倍数,显然3是3的倍数,所以P®为真。
-
另一情形是“把大壶中的水倒入小壶”。一种情况是小壶不足以容纳全部的水,即b+l >3,那么r = (b-(3一l),3)。由P(q)可知,b,l都是3的倍数,故b-(3-l)也是3的倍数,所以这时P®为真。
同理可得其他情形,这里不进行赘述。所以,根据不变性原理,我们得出结论:所有可达状态都满足P(上述已将所有可能的转移情况都分析了,都满足P,所以所有的可达状况都满足P)。而(4,l)不满足P,因此我们残酷地证明了布鲁斯死定了。
6.3 偏序正确性和终止性
弗洛伊德指出了程序验证所需的两个特性。第一个特性是偏序正确性,即过程的最终结果(如果有的话)必须满足系统的要求。
“偏序"一词指的是计算偏序关系的过程不一定会终止。偏序正确性是指如果有结果那么结果是正确的,但是过程并不总是有结果,例如可能陷入死循环。
第二个正确性特性是终止性,即过程总是会产生最终结果。
偏序正确性通常使用不变性原理证明,终止性一般使用良序原理证明。
6.3.1 快速求幂
计算a的b次方,最直接的方法就是将a乘α重复b-1次。而下面这个快速求幂程序能够显著减少乘法运算的次数。x, y,z,r表示保存数字的寄存器。赋值语句的形式为: z:= a,表示将寄存器z中的数字赋值为a。

我们断言这个程序总是会终止,而且结果是 y = a b y = a^b y=ab。
对状态机建模如下:
- 状态::= R × R × N
- 初始状态::(a,1,b)
- 状态转移规则

保持不变式P((x,y,z))定义为
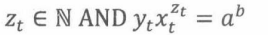
要通过 P ( ( x , y , z ) ) P((x,y,z)) P((x,y,z))成立推出 P ( ( x t , y t , z t ) ) P((x_t,y_t,z_t)) P((xt,yt,zt))成立,证明如下:
当z为偶数时:
当z为奇数时:
以上两种情况成立,所以P是保持不变式。
现在,证明偏序正确性就很简单了:当这个快速求幂程序终止时,寄存器y产生结果 a b a^b ab。由于1· a= ab,所以初始状态(a,1,b)满足P。根据不变性原理,P对所有可达状态恒为真。而只有当z = 0时,程序才会终止。既然终止状态(x, y,0)是可达的,那么 y = y x 0 = a b y = yx^0 = a^b y=yx0=ab。
它是偏序正确的,但是快在哪里呢?事实上,计算 a b a^b ab所需的乘法运算的次数大约等于b的二进制数表示形式的长度,即 l o g b 2 n logb2^n logb2n,而原始方法则需要b-1次。
6.3.2 派生变量
刚才证明终止性的时候,我们为状态赋予了一个非负整数度量值,一般称其为状态的“规模”。显然,状态的规模随着每一次状态转移逐渐减小。根据良序原理,状态的规模不可能无限减小。一旦状态机到达最小规模状态,就不再发生任何转移,即过程终止。
通常来说,对状态进行赋值——不一定是非负整数,也不一定随着状态转移而减小——在算法分析中往往很有用,类似于物理学中的势函数。在计算过程中,这样的状态赋值称为派生变量。
优势函数:优势函数表达在状态s下,某动作a相对于平均而言的优势。数量关系来看,就是随机变量相对均值的偏差。
**定义6.3.1:**派生变量f:状态→R是严格递减的( strictly decreasing ),当且仅当
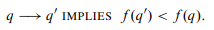
状态→R是弱递减的( weakly decreasing),当且仅当
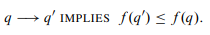
同理可以定义严格递增和弱递增的派生变量。
**定理6.3.2:**如果状态机的派生变量f的取值范围是N且严格递减,那么从起始状态q开始的执行长度不超过f(q)。
6.4 稳定的婚姻
**流氓情侣:**如果一对男女不是夫妻、比起原配他们更加爱着彼此,我们称之为流氓情侣。
如下图,Brand和Angelina是一对流氓情侣。
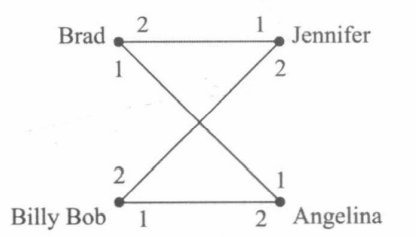
流氓情侣的存在是不好的,会影响他人婚姻的稳定。反之,如果不存在流氓情侣,那么对任何一对不是夫妻的男女,他/她一定爱配偶胜过对方,从而彼此不会出现婚外情。
**定义6.4.1:**稳定的配对不存在流氓情侣。
对任意一组男性和女性来说,总是存在稳定的婚姻配对。有一个简单的算法可以产生稳定配对、我们通过保持不变式来理解和说明这个讨程。
6.4.1 配对仪式
我们将寻找稳定配对的过程称为配对仪式。这个过程往往会持续几天。第一天,每个男性对所有女性有一个偏好列表,同样每个女性对所有男性也有一个偏好列表。接下来的每一天:
**上午:**男性每天上午向偏好列表最顶端的女生表白,
**下午:**女性每天下午在当天和他表白的男生中和以往他已经接收的那一个男生中选择一个她最喜欢的,暂时接受。对于其他则直接拒绝。
**晚上:**男生将今天拒绝过他的女生从偏好列表中删除。
**终止条件:**当每个女性至多存在一个追求者时,配对仪式终止。这时,每个女性都会与她的追求者结婚,如果她有追求者的话。
对于以上配对仪式,我们要证明三个问题
- 配对仪式最终一定会到达终止条件。
- 每个人都会结婚。
- 最终的婚姻配对是稳定的。
6.4.2 我们结婚吧
现在我们证明配对仪式一定会终止,最终每个人都会结婚。
只要配对仪式没有终止,那么当天一定至少存在一个男性,从他的偏好列表里剔除一个女性。(每一个女生只能暂时占据一个男生,所以当有男生没有被暂时接受时,他就会根据偏向表不断地表白。最坏的情况他会跟所有的女生表白,总会有一个女生接受他)假设初始状态时,有n位男性和n位女性,那么对这n个男性来说,每个男性的名单中有n个女性,共计 n 2 n^2 n2条记录。由于女性永远不会被加入名单,所以每天的记录总数是递减的,因此配对仪式最多只持续 n 2 n^2 n2天。
6.4.3 他们从此幸福地生活在一起
定义谓词P:对任意女性w和男性m,如果w被m从偏好列表中剔除,则w一定有一个比m更好的追求者。
**推论6.4.2:**在配对仪式中,P是保持不变式。
**证明:**上式显然成立,只有w碰见一个比m更好的,他才会拒绝m,w才会被m从偏好列表中删除。
**定理6.4.3:**在配对仪式中,每个人最后都会结婚。
**证明:**我们用反证法进行证明,假设到最后一天,Bob(男)还没有结婚。也就是说,Bob没有向任何人求爱,他的偏好列表一定为空。因此,每一个女性都被他从名单中剔除了,而由于P为真,即每一个女性都有一个比 Bob更好的追求者。另一方面,由于这是最后一天,每一个女性应该只有一位追求者,即她们将要结婚的对象。考虑到男女数量相同,如果所有的女性都会结婚,那么男性亦然,这与假设Bob没有结婚不符。
**定理6.4.4:**配对仪式产生的是稳定婚姻。
**证明:**令Brad(男)和Jen(女)分别是最后一天没有婚配的男女。我们需要证明他们不是流氓情侣,进而可知所有婚姻都是稳定的。下面分两种情况讨论。
**情形1:**在最后一天,Jen不在 Brad 的名单中。根据不变式P,Jen必然有一个比起 Brad她更喜欢的追求者(即她的老公)。所以Jen不会跟 Brad私奔——即他们不是流氓情侣。
**情形2:**在最后一天,Jen在 Brad的名单中。Brad依据名单上的偏爱顺序选择女性,那么比起Jen他一定更喜欢他的妻子。所以他也不会跟Jen私奔——即他们不是流氓情侣。
6.4.4 竟然是男性
在以上的配对过程中,男性比女性更具有优势,证明如下:
**定义6.4.5:**已知男性和女性的偏好,如果一对男女结合的婚姻是稳定的,那么一方是另方的可行配偶。
**定义6.4.6:**令Q表示谓词:对任意女性w和男性m,如果w被m从名单中剔除,那么w不是的可行配偶。
**引理6.4.7:**在配对仪式中,Q是保持不变式。
**证明:**假设Q在配对过程中的某一时刻为真,Alice (女)正要被Bob(男)从名单中剔除。我们断言Alice一定不是Bob的可行配偶。因此,Alice被剔除以后,Q仍然成立,说明Q是不变式。
**定义6.4.8:**一个人的最佳配偶是他们最喜欢的可行配偶,最差配偶是他们最不喜欢的可行配偶。
**证明:**如果最后一天 Bob娶了Alice,那么在Bob的名单上,所有排在Alice前面的女性都被剔除了,那么根据属性Q,这些女性都不是Bob的可行配偶。因此,Alice是排名最靠前的可行配偶,即Alice是 Bob的最佳配偶。
另一方面,由于Bob喜欢Alice超过其他任何潜在的妻子,如果比起 Bob,Alice更不喜欢她的老公,那么Alice和 Bob就成了流氓情侣。因此,Bob一定是Alice最不喜欢的可行配偶。
6.4.5 应用
配对仪式在现实中被用于将医学院的毕业生分配至医院,这里医院和毕业生就相当于男性和女性的角色。
所有排在Alice前面的女性都被剔除了,那么根据属性Q,这些女性都不是Bob的可行配偶。因此,Alice是排名最靠前的可行配偶,即Alice是 Bob的最佳配偶。
另一方面,由于Bob喜欢Alice超过其他任何潜在的妻子,如果比起 Bob,Alice更不喜欢她的老公,那么Alice和 Bob就成了流氓情侣。因此,Bob一定是Alice最不喜欢的可行配偶。
6.4.5 应用
配对仪式在现实中被用于将医学院的毕业生分配至医院,这里医院和毕业生就相当于男性和女性的角色。
此外不足为奇的是,配对仪式算法还被用于不止一个大型相亲网站。





















 1444
1444











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








