图的遍历整理

图的遍历

图遍历又称图的遍历，属于数据结构中的内容。指的是从图中的任一顶点出发，对图中的所有顶点访问一次且只访问一次。图的遍历操作和树的遍历操作功能相似。图的遍历是图的一种基本操作，图的许多其它操作都是建立在遍历操作的基础之上。

图遍历可分为四种问题：

图的遍历可分为四类：

（1）“一笔画问题”或“欧拉路径”；

（2） “哈密尔顿问题”；

（3）“中国邮递员问题”；

（4）“旅行推销员问题”。

对于第一和第三类问题已经得到了完满的解决，而第二和第四类问题则只得到了部分解决。

1.欧拉路径

问题概述

首先是一个问题：即小学奥数中的一笔画问题，在一个图中能否用一笔画从一个顶点出发来经过所有的边，最后回到这个顶点。

这个问题是数学家欧拉在研究著名的德国哥尼斯堡七桥问题时发现的，流经哥尼斯堡的普雷格尔河中有两个岛，两个岛与两岸共4处陆地通过7座杨 彼此相联。7桥问题就是如何能从任一处陆地出发，经过且经过每个桥一次后回到原出发点。

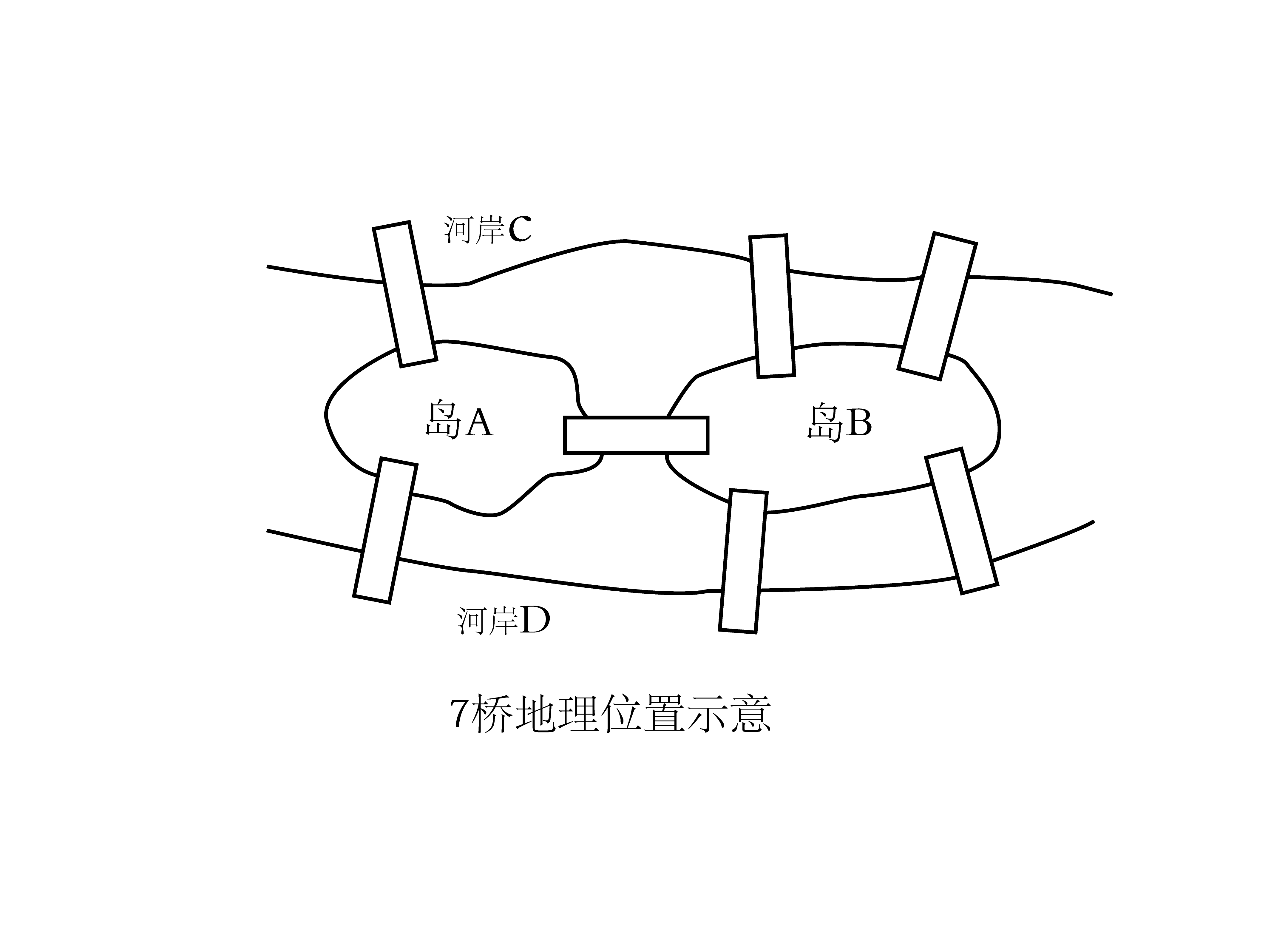
这个问题可抽象为一个如图b所示的数学意义上的图，其中4个结点分别表示与4块陆土Il 对应，如结点C对应河岸C，结点A对应岛A等，而结点之间的边表示7座桥。

欧拉通过研究这个问题，提出了几个重要的概念：

• 欧拉回路：从图上一个点u出发不重复地经过每一条边后，再次回到点u的一条路径。
• 欧拉路径：从图上一个点u出发不重复地经过每一条边的一条路径（不必回到点u）。
• 欧拉图即存在欧拉回路的图
• 半欧拉图存在欧拉路径的图。

求解算法思想

首先需要了解相关的定理：

（1）无向图欧拉回路的判定：图G为连通图，所有顶点的度为偶数。

（2）无向图欧拉路径的判定：图G为连通图，除有2个顶点度为奇数外，其他顶点度都为偶数。

（3）有向图欧拉回路的判定：图G的基图联通，所有顶点的入度等于出度。

（4）有向图欧拉路径的判定：图G的基图联通，存在起点u的入度比出度小1，v终点入度比出度大一，其余所有顶点的入度等于出度。

(忽略有向图所有边的方向，得到的无向图称为该有向图的基图)

求解是否含有欧拉路径的算法一般有两种：Fluery算法和Hierholzer算法。这里介绍Fluery算法。

Fluery算法

设G为一无向欧拉图，求G中一条欧拉回路的算法为：

1. 任取G中一顶点V0，令P0=V0；

2. 假设沿路径Pi=v0e1v1e2v2…eivi走到顶点vi，按下面方法从E(G)-{e1,e2,e3…ei}中选择ei+1:

   a.ei+1与vi相关联；

   b.除非无别的边可供选择，否则ei+1不应该是Gi=G-{e1,e2,e3…ei}中的桥。

3. 当2不能继续进行时算法停止。

   可以证明当算法停止时，得到的简单回路Pm为G中的一条欧拉回路。

(桥：一个边从无向图删除后图不再连通，这个边即为桥，也称割边)

举例说明

如图：

其中一个欧拉路径为4 5 8 7 6 8 9 1 5 3 2 4 6

假设我们走路径4 6 8 5，在5处有3种选择：(3,4,1)但是只能走3 4，因为根据算法第二步当前往顶点1时，边集加入边5,1 此时去除已走边，图为

此时如果走5,1边，剩下的图将变成不连通图，即边(5,1)为割边。以此类推。

算法具体步骤

基于DFS实现，首先运用DFS判断图是否是一个连通图，若图连通，则根据欧拉图定理2：除有2个顶点度为奇数外，其他顶点度都为偶数。判断图中奇数度的点是否为2个或0个，若为2个则有欧拉路径，如果0个则有欧拉回路，对于欧拉路径，我们选择二个点中之一作为DFS起点。运用栈作为物理存储结构。

//dfs
void dfs(int x) {
    st[top++] = x;
    for (int i = 1; i <= N; ++i) {
        if (graph[x][i]) {
            graph[x][i] = graph[i][x] = 0; // 删除此边
            dfs(i);
            break;
        }    
    }
}
//fleury
void fleury(int ss){
    int bridge;
    top=0;
    stk[top++] = ss; // 将起点放入Euler路径中
    while (top > 0) {
        brige = 1;
        for (int i = 1; i <= N; i++) { // 试图搜索一条边不是割边（桥） 
            if (graph[st[top-1]][i]) {
                brige = 0;
                break;
            }
        }
        if (brige) { // 如果没有点可以扩展，输出并出栈
            printf("%d ", st[top--]);
        } else { // 否则继续搜索欧拉路径
            dfs(st[top--]);
        }
    }
}

性能分析

单独分析Fleury算法时间复杂度为$O(|E(G)|)$

Fleury算法需要基于DFS实现，用邻接矩阵存储图，DFS时间复杂度为$O(n^2)$，Fleury算法总的时间复杂度为$O(n^2)$。

2.哈密尔顿问题

问题概述

欧拉路径问题是寻找一条路径能够遍历图中所有的边，而哈密尔顿问题是在寻找一条遍历图中所有点的基本路径。

在无向图G=<V,E>中，遍历G中每个顶点一次且仅一次的路径称为哈密尔顿路径，遍历G中每个顶点一次且仅一次的回路称为哈密尔顿回路。具有哈密尔顿回路的图称为哈密尔顿图。哈密尔顿问题是一类问题的总称。

求解算法思想

由于哈密尔顿问题被证明为一个NP问题，即非多项式问题，时间复杂度为$O(K^N)$。

首先需要判断一个图是否为哈密尔顿图，也就是是否存在哈密尔顿路径，但是证明找到一个图是否为哈密尔顿图的非平凡充要条件：

1. 若图的最小度不小于顶点数的一半，则图是哈密顿图；
2. 若图中每一对不相邻的顶点的度数之和不小于顶点数，则图是哈密顿图。

若图为汉密尔顿图，可以运用一种算法思想：

1. 从某个顶点v开始，遍历访问所有相邻顶点。
2. 如果相邻顶点u被访问过，但图中的其他顶点还存在没有访问的顶点，则进行回溯，同时让已访问的顶点v未被访问。
3. 重复1,2步骤，直到满足相邻顶点访问过且其为初始顶点，且图中所有顶点都被访问过。

以上哈密尔顿回路的求解方法，并不需要遍历所有顶点组成的路径全排列，在两个顶点之间没有边的情况下，则不会形成一条路径，也就是剪枝。

举例说明

如图

从顶点0开始访问图，开始遍历相邻顶点，假设路径为0-1.

继续dfs路径为0-1-2，现在下一步dfs要访问0，但是0已经被访问过了，现在已经满足哈密尔顿回路的第一个条件，从起点回到了起点。

但是图中还有剩余顶点没有被访问，此时需要回溯操作，同时将此时访问的顶点标记为没有访问过。这样做的原因是: 此时搜索的路径是一条死路, 需要回退并重新开始搜索。而回退的方式就是利用深度优先搜索的回溯特性, 重新搜索则需要将之前搜索过程中标记的访问的状态置为空。

回溯到1后dfs，由于相邻顶点3还未访问，访问3，形成路径0-1-3，此时与上方情况相同，形成死路，需要回溯，将1标记为未访问，返回到顶点0开始dfs，新路径为0-2，以此类推，可以得到路径0-2-1-3或0-3-1-2。

算法具体步骤

1. 从某个顶点v开始，DFS访问所有相邻顶点。
2. 如果相邻顶点u被访问过，但图中的其他顶点还存在没有访问的顶点，则进行回溯，同时标记顶点v未被访问。
3. 重复1,2步骤，直到满足相邻顶点访问过且其为初始顶点，且图中所有顶点都被访问过。

void isHamilton(int D[],int n){
    int isHp=1,isHg=1;
    int i=0,j=0;
    for(int i=0;i<n;i++){
        for(j=0;j<n;j++){
            if(D[i]+D[j]<(n-1)){
                isHp=0;isHg=0;break;
            }
            else if(D[i]+D[j]<n){
                isHg=0;break;
            }
        }
        if(isHp==0){break;}
    }
    if(isHg==1){printf("为哈密尔顿图\n");}
    else if((isHp==1)&&(isHg==0)){printf("存在哈密尔顿路\n");}
    else {cout<<"不存在哈密尔顿路"<<endl;}
}

性能分析

此算法为暴力搜索，时间复杂度为$O(n!\ast n)$，我们可以利用状态压缩动态规划，我们可以将时间复杂度降低到$O(n^2\ast n^3)$ ，具体算法是建立方程f(i,S,j)，表示经过了i个节点，节点都是集合S的，到达节点j时的最短路径。每次我们都按照点j所连的节点进行转移。

3.中国邮递员问题(CPP)

问题概述

邮递员在某一地区的信件投递路程问题。邮递员每天从邮局出发，走遍该地区所有街道再返回邮局，问题是他应如何安排送信的路线可以使所走的总路程最短。用图论的语言描述，给定一个连通图G，每边e有非负权)，要求一条回路经过每条边至少一次，且满足总权最小。

求解算法思想

在一个具有非负权的赋权连通图G中，找出一条权最小的环游，这种环游称作最优环游。

如果是一个欧拉图，可以直接运用Fleury算法求出欧拉回路，可以得到解答。

当不是欧拉图时，有的边不得不通过大于等于2次，此时需要求解哪些边通过大于等于2次可以让权值最小。

在1973年埃德蒙兹（J.Edmonds）和约翰逊（E.L.Johnson)给出了多项式次时间解法和证明，一般解法可以归纳为：

1. 将重复走过的边作为重边添加到图中。
2. 添加重边成为欧拉图。
3. 令添加的边权和最小。
4. Fleury算法找到欧拉回路。

我们添加重边的目标为消除奇次顶点，这样才能使它变成一个欧拉图。

重边的添加方法：

• 连接所有k个奇次顶点对的k条无公共边的最短路径。
• 边权和最小

算法具体步骤

Edmonds-Johnson算法：

1. 找到所有2k个奇度顶点间的最短路径。
2. 构造一个完全图$K_{2}k$:顶点为2k个奇度顶点，边权为最短路的边权和，运用Dijkstra算法。
3. 找到完全图的最小权完美匹配M。
4. 沿M对应的最短路径添加重边

CPP问题解决方法

1. 判断图中奇度顶点个数，若为欧拉图，直接运行Fleury算法。
2. 若不为欧拉图，运行Edmonds-Johnson算法构造新的欧拉图，运行Fleury算法。

void Floyd (vector<vector<int>>& graph, int N) {
        for (int k=1; k<=N; ++k) {
            for (int i=1; i<=N; ++i) {
                for (int j=1; j<=N; ++j) {
                    if (i == j) {
                        continue;
                    }
                    if (graph[i][k]!=-1 && graph[k][j]!=-1) {
                        graph[i][j] = graph[i][j]==-1 ? graph[i][k]+graph[k][j] : min (graph[i][j], graph[i][k]+graph[k][j]);
                    }
                }
            }
        }
    }
int shortestPath (vector<vector<int>>& graph, vector<int>& dev, int N) {
        Floyd (graph, N);
        vector<int> odds;
        odds.push_back(0);
        for (int i=1; i<=N; ++i) {
            if (dev[i]&1) {
                odds.push_back(i);
            }
        }
        int res = 0;
        int ods = odds.size()-1;
 
        vector<int> dp((1<<ods), -1);
        dp[0] = 0;
        for (int i=0; i<(1<<ods); ++i) {
            int x = 1;
            while ((1<<(x-1)) & i) {
                ++x;
            }
            for (int y=x+1; y<=ods; ++y) {
                if ((1<<(y-1)) & i) {
                    continue;
                }
                dp[i|(1<<(x-1))|(1<<(y-1))] = dp[i] != -1 && graph[odds[x]][odds[y]] != -1 ? dp[i|(1<<(x-1))|(1<<(y-1))] == -1 ? dp[i]+graph[odds[x]][odds[y]] : min(dp[i|(1<<(x-1))|(1<<(y-1))], dp[i]+graph[odds[x]][odds[y]]) : dp[i|(1<<(x-1))|(1<<(y-1))];
            }
        }
        for (int i=0; i<(1<<ods); ++i) {
            cout << dp[i] << " ";
        }
        cout << endl;
        cout << dp[(1<<ods)-1] << endl;
        return dp[(1<<ods)-1];
    }

4.卖货郎问题(TSP)

问题概述

给定一系列城市和每对城市之间的距离，求解访问每一座城市一次并回到起始城市的最短回路。

TSP是一个NP难问题。

图论描述：求赋权连通图中经过每个顶点恰一次且全权和最小的边

求解算法思想

最容易想到的是递归遍历，但是最差时间复杂度为$O(n!)$，所以我们运用贪心算法的思想，寻找局部最优解，我们可以从一个城市即顶点开始每次选择一个城市，直到所有的城市被走完，每次选择下一个城市我们只考虑当前所走过的路径最短。我们还可以运用近似算法，高效的找出最优解。近似算法有临近点法，最小生成树法，最小权匹配法以及Kernighan-Lin方法。

临近点法的基本思路是总是贪心地选择最近的未访问邻接点前行。

举例说明

假设从A点出发，我们寻找邻接点中权值最小的边即a-b或a-e。

假如选择a-b，在b点继续选择即b-d，以此类推，最后可以得到总路径权值和=5+7+8+16+12=48.

算法具体步骤

针对TSP问题，使用临近点法的求解的过程为：
1.从某一个城市开始，每次选择一个城市，直到所有的城市被走完。
2.每次在选择下一个城市的时候，只考虑当前情况，保证迄今为止经过的路径总距离最小。

// 这个城市k是否出现过了
bool isShowed(int k) {
    
    for (int i = 0; i < cityNum ; i++) {
        if (s[i] == k) {
            return YES ;
        }
    }
    return NO;
}
void clostCityDistance(int currentCity) {
// 距离当前城市最近的下一个城市
 int tempClosest = 9999;
 for (int i = 0; i < cityNum; i++) {
 	if ( isShowed(i) == NO && distance[i][s[currentCity]] <tempClosest ) {
 		tempClosest = distance[i][s[currentCity]] ;
 		s[currentCity+1] = i ; 
 	}
// 判断是否应该结束了,  如果s[]中有一个还是初始值-1的话,说明不该结束,继续寻找下一个城市.
 bool shouldFinish = YES;
    for (int i = 0; i < cityNum; i++) {
        if ( s[i] == -1 ) {
            shouldFinish = NO ;
        }
    }
    if (shouldFinish == NO) {
        clostCityDistance(s[currentCity+1]);
    } else {
        return ;
    }
}
// 剩下就是初始条件了, 初始化出发的城市,可以是0,1,2,3任意一个
      s[0] = 0; // s[0] = 1 ;
    clostCityDistance(s[0]);

性能分析

邻接点法本质是贪心算法，此算法性能与初始点有关，最差情况下要到第n个点才能求得最短路径，时间复杂度为$O(v^2)$