密码学实验二

MILLER-RABIN检测(转)

Miller-Rabin检测是目前应用比较广泛的一种

二次探测定理:如果p是一个素数,且0<x<p,则方程x^2%p=1的解为:x=1或x=p-1
费马小定理：a^(p-1) ≡ 1(mod p)

这就是Miller-Rabin素性测试的方法。不断地提取指数n-1中的因子2，把n-1表示成d*2^r（其中d是一个奇数）。那么我们需要计算的东西就变成了a的d*2^r次方除以n的余数。于是，a^(d * 2^(r-1))要么等于1，要么等于n-1。如果a^(d * 2^(r-1))等于1，定理继续适用于a^(d * 2^(r-2))，这样不断开方开下去，直到对于某个i满足a^(d * 2^i) mod n = n-1或者最后指数中的2用完了得到的a^d mod n=1或n-1。这样，Fermat小定理加强为如下形式：

尽可能提取因子2，把n-1表示成d*2^r，如果n是一个素数，那么或者a^d mod n=1，或者存在某个i使得a^(d*2^i) mod n=n-1 ( 0<=i<r ) （注意i可以等于0，这就把a^d mod n=n-1的情况统一到后面去了）

定理:若n是素数,a是小于n的正整数,则n对以a为基的Miller测试,结果为真.
Miller测试进行k次,将合数当成素数处理的错误概率最多不会超过4^(-k)

# -*- coding:UTF-8 -*-
# Miller-Rabin素数检测算法
 
import math
def relatively_prime(a,b): # a > b
	while b != 0:
		temp = b
		b = a%b
		a = temp
	if a==1:
		return True
	else:
		return False
def  millerRabin(num):
	if num%2 ==0:
		return False
	flag = True
	Subsquare = 0
	temp = num - 1
	while True:
		temp = temp / 2
		Subsquare += 1
		if temp % 2 != 0:
			break
	b=[] # 存放所求整数（num）的原根
	count = 0
	for i in range(2,num-1):# g^(P-1) = 1 (mod P)
		if relatively_prime(num,i):
			b.append(i)
			count += 1
			if count == 5:	# 控制检测次数
				break
	for i in b:
		two = 0
		while True:
			if (i**temp)**(2**two)%num == 1 or (i**temp)**(2**two)%num == num-1:
				flag = True
				break
			else:
				two += 1
				if two == Subsquare:
					flag = False
					break
		if flag == False:
			break # 如果存在一次不满足条件，则退出循环
	return flag
num = input(u"请输入要进行Miller-Rabin算法检测的数：")
if millerRabin(num):
	print u"{0}大概率是素数".format(num)
else:
	print u"{0}是合数 ".format(num)

原根(转)

1.原根定义

（1）假设一个数g对于P来说是原根，那么g^i mod P的结果两两不同,且有 1<g<P, 1<i<P,那么g可以称为是P的一个原根

简单来说，g^i mod p ≠ g^j mod p （p为素数）

 

（2）如果从欧拉函数的角度定义，我们可以先引进一个概念：阶

关于阶可以看这里：https://blog.csdn.net/a27038/article/details/77203892
此时给原根下定义：

如果 a 与 n 是互质的整数且n>0，那么当 ordna=φ(n)时，称aa为模n的原根。 

 

有个结论：如果g是P的原根，就是g^(P-1) = 1 (mod P)当且仅当指数为P-1的时候成立.(这里P是素数).

证明（转）：

首先看一下欧拉定理：

欧拉定理（也称费马-欧拉定理或欧拉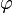函数定理）是一个关于同余的性质。欧拉定理表明，若为正整数，且互素（即），则

因此，在时，定义对模的指数为使成立的最小的正整数。由前知 一定小于等于 ，若，则称是模的原根。

 

2.如何求解：

一、枚举

从2开始枚举，然后暴力判断g^(P-1) = 1 (mod P)是否当且当指数为P-1的时候成立

而由于原根一般都不大，所以可以暴力得到.

二、讲究方法

定理：如果模m有原根，那么他一共有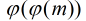个原根。 
定理：如果p为素数，那么素数p一定存在原根，并且模p的原根的个数为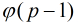个。 
定理：假设m是正整数，a是整数，如果a模m的阶等于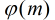，则称a为模m的一个原根。 
模m有原根的充要条件：m=2,4,P^a,2*P^a……. 
求模素数P的原根的方法：对P-1素因子分解，即P-1=(P1^a1)(P2^a2)…..(Pk^ak)。，若恒有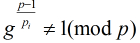成立，那么g就是P的原根(对于合数而言,只需要把p-1换成即可)