数学思考【1】关于弧度制

---

写在前面：
最近在重新反刍一些知识，上学时候只知道填鸭考试，却没有深入的去思考一些东西。

---

1.什么是弧度制和角度制

机械设计中，电机计算中，经常要用的弧度和角度的转换，以前总是感觉很麻烦，最近去思考，为什么非要用弧度，数学家为什么一定要麻烦一遭呢？

角度制：

我们初识接受的教育就是一圈360度，习惯了用30°，45°，60°，90°，180°，360°，这个六十进制表示的角度制。
也有很多的应用场景：

• “态度发生一百八十度大转弯”表示态度改变很大，180度翻转，前后矛盾，戏剧变化；
• 监控摄像头“360度无死角”，360度监控视野，或者服务全方位；
• 当代小说的经典句式“四十五度角仰望天空”，表达理想与现实的分界，刻画青春期的心理情绪。
  网上的关于360的来源的说法，可能源于他们观测到的太阳每年运行约360天的天文规律，其实研究过古天文就会发现，360这个数字在天文行星的运行规律中并没有出现，但是很接近，这里面涉及到一个秘传，就是360协调周期的问题，这个不是本文的重点，就不深入了。
  然而，这种基于数字神秘主义的划分，始终与圆本身的几何特性存在隔阂，他是一个定义，在数理上和圆并没有联系。

比如60°+sin30°=60°+0.5，如果不学习弧度制，就无法继续计算！因为单位不统一，根本上就是两个东西，甚至我可以定义圆周不是360度，可以是123度这种奇怪的数字。

弧度制

18世纪，当数学家们试图建立微积分与三角函数的桥梁时，角度制的局限性逐渐显露。瑞士数学家欧拉发现，当用360度制计算三角函数导数时，总要带着繁琐的换算系数。他意识到问题的根源在于：角度制是用"人为分割的数值"而非"几何本质"来描述角的大小。

真正的突破来自一个简单的几何观察：当半径为r的圆，有一动点在圆周上运动时，走过的长度就是弧长，与半径r的比值，对应一个确定的圆心角的大小。
或者换一个角度说，当圆心角变化的时候，对应的弧长在变化，说明圆心角一定和弧长有关系，但是弧长的变化，又和半径尺寸有关系，肯定是半径越大，弧长越长。
这说明圆心角，和弧长和半径有关系（想象一个圆也就这两个因素了），但是是怎么推出来弧长/半径 = 确定的圆心角呢？
这里面我暂时还没有找到答案，应该是从三角函数那边过来的。

这个比值不仅消除了圆的尺寸影响，更天然地连接了直线与曲线——当r=1时，弧长就是角度本身！这种以半径丈量圆弧的思维，最终被命名为"弧度制"。 数学推算的奇妙之处在于，我们可以通过数学等式，来把干扰因素去除，找到真正的最本质的东西！

假如圆心角AOB旋转了360°，那么弧长是2πr，计算出弧度是2π。见下图。

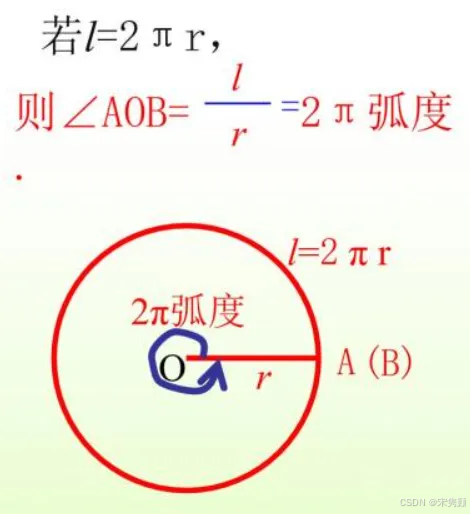
这样360°=2π弧度，180°=π弧度，90°=π/2弧度，45°=π/4弧度，60°=π/3弧度，30°=π/6弧度。这样让角度变成了实数，也意味着，角度和数学世界产生了链接！
60°+sin30°=60°+0.5=π/3+0.5=3.14/3+0.5≈1.05+0.5=1.55
令人惊叹的是，弧度制让圆周率π成为了角度转换的天然媒介，这种设计暗示着圆与直线之间的深刻联系。当科学家在量子力学中使用复平面，或在相对论中处理时空曲率时，弧度制提供的几何直觉仍在持续发光。
图片
总结：弧度制的诞生不仅是数学工具的创新，更展现了人类认知模式的进化。它告诉我们：最优雅的数学语言往往诞生于对事物本质的洞察。