AVL树是带有平衡条件的binary_search_tree,要求每个节点的左子树和右子树的高度相差不超过1
插入一个节点可能破会avl的平衡性,所以我们要在插入后对不满足条件的部分进行修正
总的来说需要修改的情形有这么几种:
1,连续两个节点朝一个方向倾斜–single ronate:
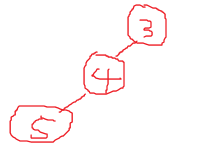
这种情况下我们使用一次单旋转:
找出三个元素中的中间值作为节点,其他两个当作树叶
就相当于把3和4进行一次”旋转“如下图:
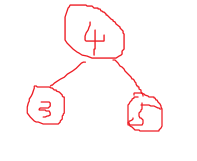
这样就将高度降低了1
2,两个节点倾斜的方向相反:
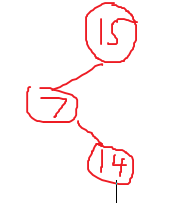
如此也是像上一个一样,找出中间值然后作为父节点:
由于形式不一样,我们需要旋转两次,先把14和7旋转,再把14和15旋转
我们称之为左右双旋转
3,上面讨论的都是简单的情况,但是有时候我们要旋转的节点和其他节点又有联系:也就是说我们要处理节点的分支
下面举几个例子:
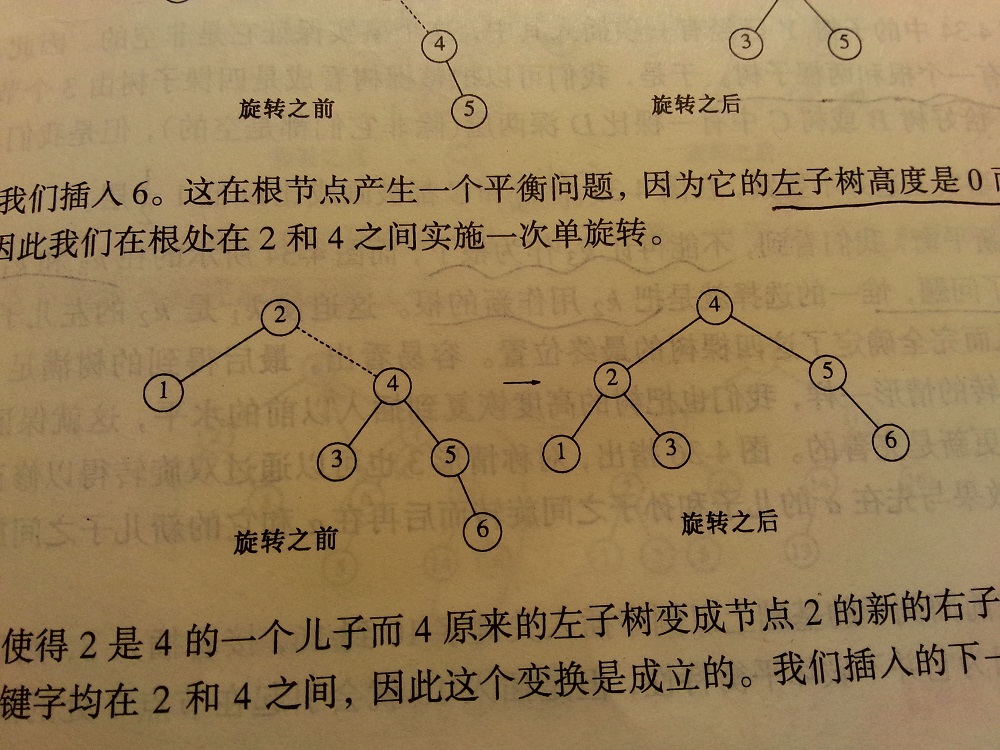
在这里我们首先要确定调整哪个节点:看哪个节点的左右子树高度差距大于1,得到2,此时我们把5,6节点看成是一个整体节点,我们要把2,4,5+6这三个节点进行调整,对应情况1,单旋转一次:
将4作为父节点->这种情况下4还有一个高度为1的矮一些的树,我们将其改为原先父节点的右子树,如上图
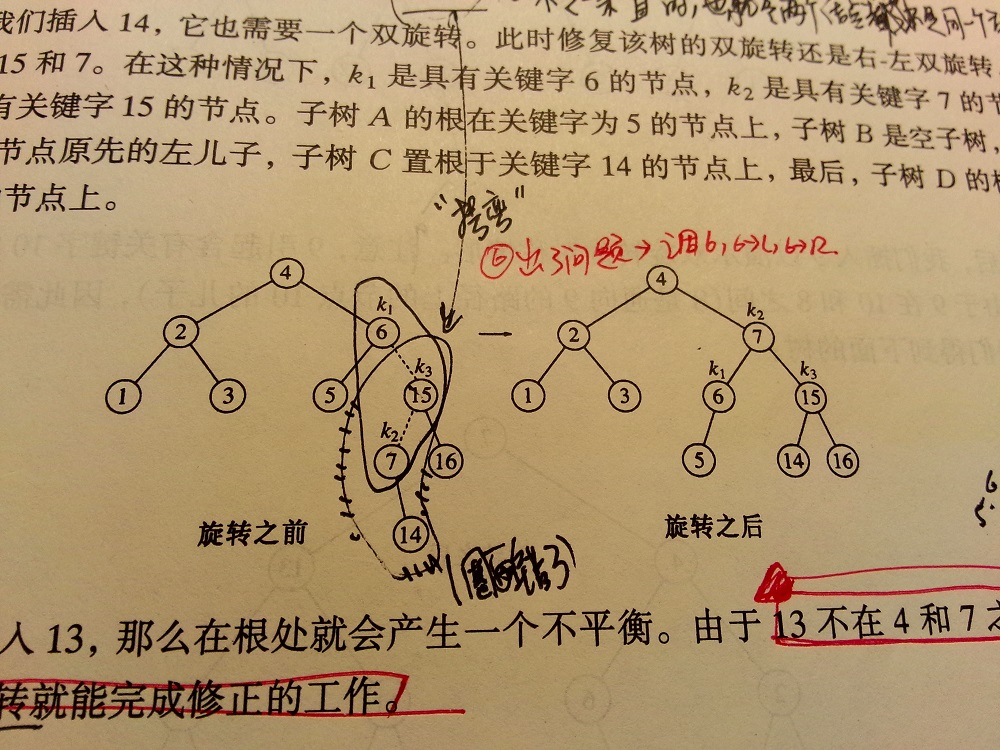
这里的情况和上图稍有不同的是要确定是调整6还是调整4,因为这两个树节点的左右子树均不符合
这种情况下我们选择调整小的(或从下往上调整)
所以我们调整6:
这里6的右子树和它需要一次双旋转,同样,我们将6,15,7进行处理
7成为父节点,7的右子树继续成为7的父节点的左子树原先的父节点成为新父节点的左子树
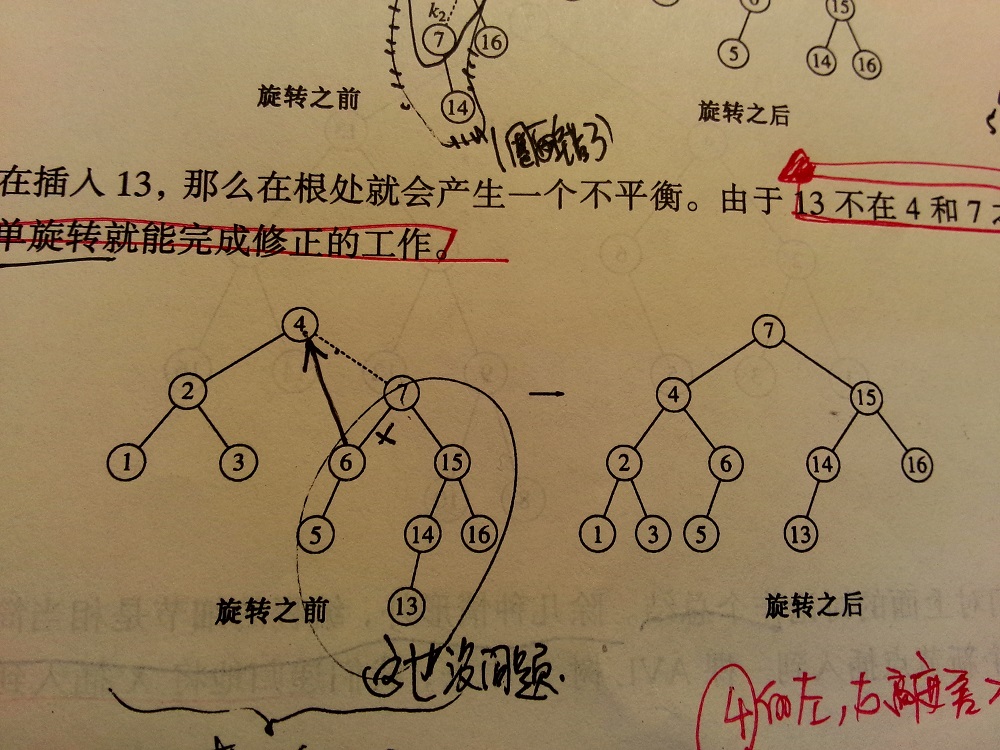
现在我们插入13,插入13引起新的不平衡,要调整的父节点为4,4的左子树(要调整的子树)父节点为7,由于13不在4和7之间,所以用但旋转就能解决问题。
(调整父节点,不平衡的子树父节点,以及根据单双旋转确定的要调整的节点)
不完整代码:
static int height(avlnode* t)
{
if (t == NULL)
return -1;
else return t->height;
}
avlnode* singleRonateWithLeft(avlnode* t)
{
avlnode* t1;
t1 = t->left;
t->left = t1->right;
t1->right = t;
t->height = max(height(t->left), height(t->right)) + 1;
t1->height = max(height(t1->left), t->height) + 1;
return t1;//new father node
}
avlnode* doubleRonateWithLeft(avlnode* t)
{
t->left = singleRonateWithRight(t->left);
return singleRonateWithLeft(t);
}
avlnode* singleRonateWithRight(avlnode* t)
{
avlnode* t1 = t->right;
t->right = t1->left;
t1->left = t;
t->height = max(height(t->left), height(t->right)) + 1;
t1->height = max(height(t1->right), t->height) + 1;
return t1;
}
avlnode* doubleRonateWithRight(avlnode* t)
{
singleRonateWithLeft(t->right);
return singleRonateWithRight(t);
}
avlnode* insert(avlnode*t, elemtype x)
{
if (t == NULL)
//alloc
;
else if (x < t->data)
{
t->left = insert(t->left, x);
//we check after "insert" is done
if (height(t->left) - height(t->right) == 2)
{
if (x < t->left->data)//go all the way left,case 1
t = singleRonateWithLeft(t);
else
t = doubleRonateWithLeft(t);
}
}
else if (x > t->data)
{
t->right = insert(t->right, x);
if (x>t->right->data)
t = singleRonateWithRight(t);
else t = doubleRonateWithRight(t);
}
t->height = max(height(t->left), height(t->right)) + 1;
return t;
}





















 60
60











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








