POJ 3783 鹰蛋问题，非常好的DP题目

题目大意：N个蛋M层楼，问至少需要多少次数可以精确确定蛋会在几楼打碎，打碎的蛋不能再用，没打碎的蛋可以继续试验。

很多人第一时间会想到二分，其实并不是，比如1个蛋100层，直接从50层开始扔，则直接碎掉了，肯定是不行的，唯一的方法就是从一楼一层层往上试。

比如现在还剩i个蛋有j层，想知道这么一个状态所需要的次数是多少，用f[i][j]表示当前状态。

暴力枚举现在的第i个蛋扔在第k层（k是暴力寻找的)，如果碎了，则现在只有i-1个蛋，我们需要在下面的k-1的层数中确定次数，状态为f[i-1][k-1]，如果没碎，则我们还剩i个蛋，我们需要在上面的j-k层中找到答案，状态为f[i][j-k]，由于是至少的次数，所以必定由f[i-1][k-1]和f[i][j-k]这两种转移过来，这两者需要取max(表示最不幸的情况)。
至于我们想求的f[i][j]，枚举k这么多个状态时，需要找到最好的一个答案，所以再对枚举的所有(min(f[i-1][k-1],f[i][j-1])+1)取max。
最后f[N][M]就是答案。
时间复杂度为O(N*M^2)。

核心代码：

for(int i=2;i<=50;i++)
	for(int j=1;j<=1000;j++){
		min1=100000000;
		for(int k=1;k<=j;k++)
			min1=min(min1,max(f[i-1][k-1],f[i][j-k])+1);
		f[i][j]=min1;
	}

完整代码：

#include<iostream>
using namespace std;
int f[60][1100];
int min1,test,t,x,y,z;
int main(){
	for(int i=0;i<=1000;i++)f[1][i]=i;
	for(int i=2;i<=50;i++)
		for(int j=1;j<=1000;j++){
			min1=100000000;
			for(int k=1;k<=j;k++)
				min1=min(min1,max(f[i-1][k-1],f[i][j-k])+1);
			f[i][j]=min1;
		}
	cin>>test;
	for(int t=1;t<=test;t++){
		cin>>x>>y>>z;
		cout<<x<<" "<<f[y][z]<<endl;
	}
	return 0;
}

参考视频：https://www.bilibili.com/video/BV1KE41137PK

方法二：
如果只有一组数据，则有个更快的方法，用f[i][j]表示当前用了i次的情况下用j个蛋最多能确定多少层，状态转移是f[i][j]=f[i-1][j-1]+f[i-1][j]+1，时间复杂度为O(N*M)。

核心代码：

for(int i=1;i<=m;i++){
	for(int j=1;j<=n;j++)
		f[i][j]=f[i-1][j-1]+f[i-1][j]+1;
	if(f[i][n]>=m){
		cout<<x<<" "<<i<<endl;
		break;
	}
}

完整代码：

#include<iostream>
using namespace std;
int test,x,n,m;
int f[1100][60];
int main(){
	cin>>test;
	for(int t=1;t<=test;t++){
		cin>>x>>n>>m;
		for(int i=1;i<=m;i++){
			for(int j=1;j<=n;j++)
				f[i][j]=f[i-1][j-1]+f[i-1][j]+1;
			if(f[i][n]>=m){
				cout<<x<<" "<<i<<endl;
				break;
			}
		}
	}
	return 0;
}

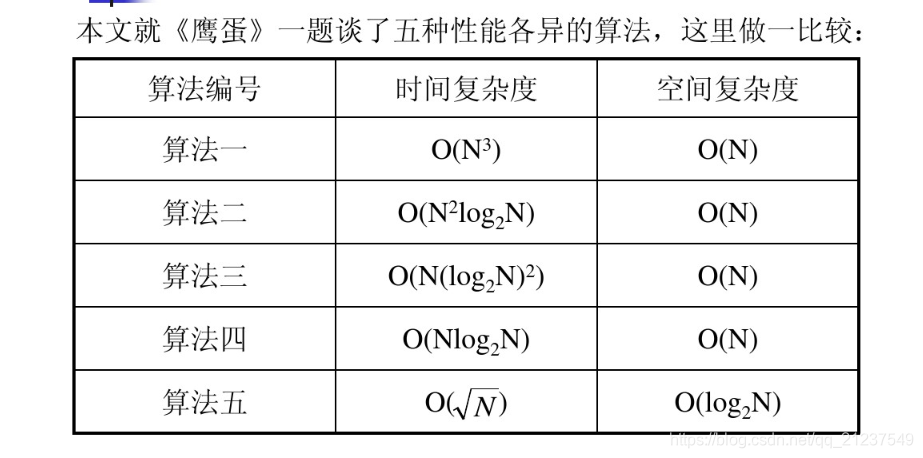
当然还有更快的sqrt(n)方法，参考国家队论文
算法合集之《从《鹰蛋》一题浅析对动态规划算法的优化》
论文地址：https://wenku.baidu.com/view/7d57940ef12d2af90242e6ac.html