有向图的遍历讨论

Directed graph traversal, orderings and applications to data-flow analysis

• 有向图遍历 排序 在数据流分析中的应用
• see details from https://eli.thegreenplace.net/2015/directed-graph-traversal-orderings-and-applications-to-data-flow-analysis/#id10
• When a directed graph is known to have no cycles, I may refer to it as a DAG (directed acyclic graph). When cycles are allowed, undirected graphs can be simply modeled as directed graphs where each undirected edge turns into a pair of directed edges.

depth first search and pre-order

Here is a simple implementation of DFS in Python

def dfs(graph, root, visitor): 
/*
    DFS over a graph.
    Start with node 'root', calling 'visitor' for every visited node.
*/
    visited = set()

    def dfs_walk(node):
        visited.add(node)
        visitor(node)                       /* 先对该节点执行visitor */
        for succ in graph.successors(node): /* successors 指子节点 */
            if not succ in visited:
                dfs_walk(succ)

    dfs_walk(root)

pre-order traversal on graphs is defined as the order in which the aforementioned（上述的） DFS algorithm visited the nodes.

there’s a subtle but important difference from tree pre-order. Whereas in trees, we may assume that in pre-order traversal we always see a node before all its successors, this isn’t true for graph pre-order. Consider this graph:

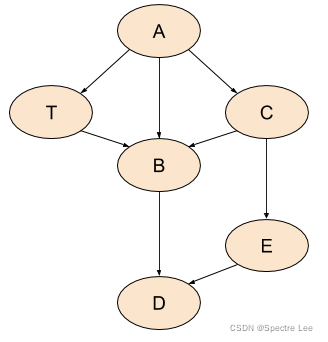
If we print the nodes in the order visited by DFS, we may get something like:A, C, B, D, E, T. So B comes before T, even though B is T’s successor

Post-order and reverse post-order

To present other orderings and algorithms, we’ll take the dfs function above and tweak it slightly. Here’s a post-order walk. It has the same general structure as dfs, but it manages additional information (order list) and doesn’t call a visitor function:

def postorder(graph, root):
    /* Return a post-order ordering of nodes in the graph. */
    visited = set()
    order = []

    def dfs_walk(node):
        visited.add(node)
        for succ in graph.successors(node):
            if not succ in visited:
                dfs_walk(succ)
        order.append(node)  /* 先将successor录入order[] 再登入node*/

    dfs_walk(root)
    return order

This algorithm adds a node to the order list when its traversal is fully finished; that is, when all its outgoing edges have been visited.

Reverse post-order (RPO) is exactly what its name implies. It’s the reverse of the list created by post-order traversal. In reverse post-order, if there is a path from V to W in the graph, V appears before W in the list. Note that this is actually a useful guarantee - we see a node before we see any other nodes reachable from it; for this reason, RPO is useful in many algorithms.

• Let’s see the orderings produced by pre-order, post-order and RPO for our sample DAG:

     Pre-order:     A, C, B, D, E, T 
     Post-order:    D, B, E, C, T, A 
     RPO:           A, T, C, E, B, D 

RPO actually guarantees that we see a node before all of its successors (again, this is in the absence of cycles, which we’ll deal with later).
逆后序遍历可以保证 对一个node的访问一定在其子节点之前

Topological sort (拓扑排序)

In fact, the RPO of a DAG has another name - topological sort. Indeed, listing a DAG’s nodes such that a node comes before all its successors is precisely what sorting it topologically means.

If nodes in the graph represent operations and edges represent dependencies between them (an edge from V to W meaning that V must happen before W) then topological sort gives us an order in which we can run the operations such that all the dependencies are satisfied (no operation runs before its dependencies).
如果图中的节点表示操作，边表示操作之间的依赖关系 ，则逆后序（拓扑排序）可以告诉我们一个顺序来保证一个节点的运行已经满足了之前的所有依赖节点。

DAGs with multiple roots 多个根节点的非循环有向图

Here’s another graph, where not all nodes are connected with each other. This graph has no pre-defined root. How do we still traverse all of it in a meaningful way?

The idea is a fairly simple modification of the DFS traversal shown earlier. We pick an arbitrary unvisited node in the graph, treat it as a root and start dutifully traversing. When we’re done, we check if there are any unvisited nodes remaining in the graph. If there are, we pick another one and restart. So on and so forth until all the nodes are visited:
选择任意一个node开始进行遍历，一个图遍历结束后，对仍然未经过的一个random node为root再次遍历

def postorder_unrooted(graph):
    /*Unrooted post-order traversal of a graph.

    Restarts traversal as long as there are undiscovered nodes. **Returns a list
    of lists**, each of which is a post-order ordering of nodes discovered while
    restarting the traversal.
    */
    allnodes = set(graph.nodes())
    visited = set()
    orders = []

    def dfs_walk(node):
        visited.add(node)
        for succ in graph.successors(node):
            if not succ in visited:
                dfs_walk(succ)
        orders[-1].append(node)
    while len(allnodes) > len(visited):

        /* While there are still unvisited nodes in the graph, pick one at random
         and restart the traversal from it.*/

        remaining = allnodes - visited
        root = remaining.pop()
        orders.append([])

        dfs_walk(root)
    return orders

and the result will be (in post-order)

[
 ['d', 'b', 'e', 'c'],
 ['j', 'f'],
 ['r', 'k'],
 ['p', 'q'],
 ['t', 'x']
]

While relative ordering between entirely unconnected pieces of the graph (like K and and X) is undefined, the ordering within each connected piece may be defined.
此时类似K and X 这种完全无连接的图是没有定义的，但有连接的部分被定义了
For example, even though we discovered T and X separately from D, B, E, C, there is a natural ordering between them. So a more sophisticated algorithm would attempt to amend this by merging the orders when that makes sense.
在随机选点时，like T and X 被分割开了，但它们和 D, B, E, C是存在自然联系的，我们可以把本身有联系的merge起来
Alternatively, we can look at all the nodes in the graph, find the ones without incoming edges and use these as roots to start from.
或者可以直接找到没有进入边的点并把它们作为起点

Directed graphs with cycles 有环有向图

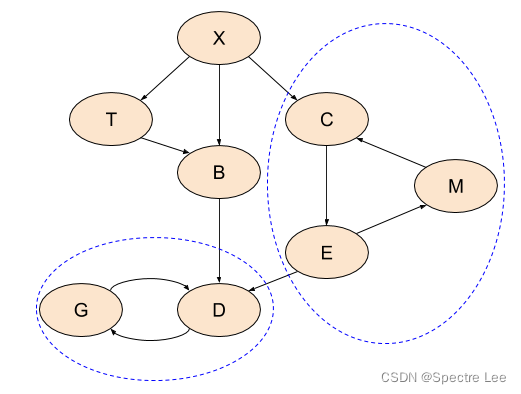
Here’s a sample graph with a couple of cycles:

In a graph with cycles, there is - by definition - no order of nodes where we can say that one comes before the other. Nodes can be visited before all their outgoing edges have been visited in post-order. Topological sort is simply undefined on graphs with cycles.
在有环图中 我们无法定义哪一个node在前。
Out post-order search will still run and terminate, visiting the whole graph, but the order it will visit the nodes is just not as clearly defined. Here’s what we get from postorder, starting with X as root:

['m', 'g', 'd', 'e', 'c', 'b', 't', 'x']

there’s no actual path from G and D to M, while a path in the other direction exists. So could we somehow “approximate” a post-order traversal of a graph with cycles, such that at least some high-level notion of order stays consistent (outside actual cycles)

Strongly Connected Components

the concept that helps us here is Strongly Connected Components (SCCs, hereafter). A graph with cycles is partitioned into SCCs, such that every component is strongly connected - every node within it is reachable from every other node. In other words, every component is a loop in the graph; we can then create a DAG of components. Here’s our loopy graph again, with the SCCs identified. All the nodes that don’t participate in loops can be considered as single-node components of themselves:

3-color DFS and edge classification

As we’ve seen above, while our postorder function manages to visit all nodes in a graph with cycles, it doesn’t do it in a sensical order and doesn’t even detect cycles. We’ll now examine a variation of the DFS algorithm that keeps track of more information during traversal, which helps it analyze cyclic graphs with more insight.
This version of graph DFS is actually something you will often find in books and other references; it colors every node white, grey or black, depending on how much traversal was done from it at any given time. This is why I call it the “3-color” algorithm, as opposed to the basic “binary” or “2-color” algorithm presented here earlier (any node is either in the “visited” set or not).
The following function implements this. The color dict replaces the visited set and tracks three different states for each node:

• Node not in the dict: not discovered yet (“white”).
• Node discovered but not finished yet (“grey”)
• Node is finished - all its outgoing edges were finished (“black”)

def postorder_3color(graph, root):
    /*
    Return a post-order ordering of nodes in the graph.
    Prints CYCLE notifications when graph cycles ("back edges") are discovered.
    */
    color = dict()
    order = []

    def dfs_walk(node):
        color[node] = 'grey'
        for succ in graph.successors(node):
            if color.get(succ) == 'grey': /* 遇到两个grey时认为有环，相当于做标记 */
                print 'CYCLE: {0}-->{1}'.format(node, succ)
            if succ not in color:
                dfs_walk(succ)
        order.append(node)
        color[node] = 'black'

    dfs_walk(root)
    return order

The edges between M and C and between G and D are called back edges. This falls under the realm of edge classification. In addition to back edges, graphs can have tree edges, cross edges and forward edges. All of these can be discovered during a DFS visit. Back edges are the most important for our current discussion since they help us identify cycles in the graph.

Data-flow analysis

In compilation, data-flow analysis is an important technique used for many optimizations. The compiler analyzes the control-flow graph (CFG) of a program, reasoning about how values can potentially change through its basic blocks.

Without getting into the specifics of data-flow analysis problems and algorithms, I want to mention a few relevant observations that bear strong relation to the earlier topics of this post. Broadly speaking, there are two kinds of data-flow problems: forward and backward problems. In forward problems, we use information learned about basic blocks to analyze their successors. In backward problems, it’s the other way around - information learned about basic blocks is used to analyze their predecessors.
在不讨论数据流分析问题和算法的细节的情况下，我想提到一些与本文前面的主题密切相关的观察结果。 广义上讲，有两种数据流问题:前向和后向问题。 在正向问题中，我们使用了解到的关于基本块的信息来分析它们的后继。 而在反向问题中，情况正好相反——从基本块中学到的信息被用来分析它们的前辈。
Therefore, it shouldn’t come as a surprise that the most efficient way to run forward data-flow analyses is in RPO. In the absence of cycles, RPO (topological order) makes sure we’ve seen all of a node’s predecessors before we get to it. This means we can perform the analysis in a single pass over the graph.
For a similar reason, the most efficient way to run backward data-flow analysis is post-order. In the absence of cycles, postorder makes sure that we’ve seen all of a node’s successors before we get to it.
One final note: some resources recommend to use RPO on a reverse CFG (CFG with all its edges inverted) instead of post-order on the original graph for backward data-flow. If your initial reaction is to question whether the two are equivalent - that’s not a bad guess, though it’s wrong. With cycles, the two orders can be subtly different. Consider this graph, for example:

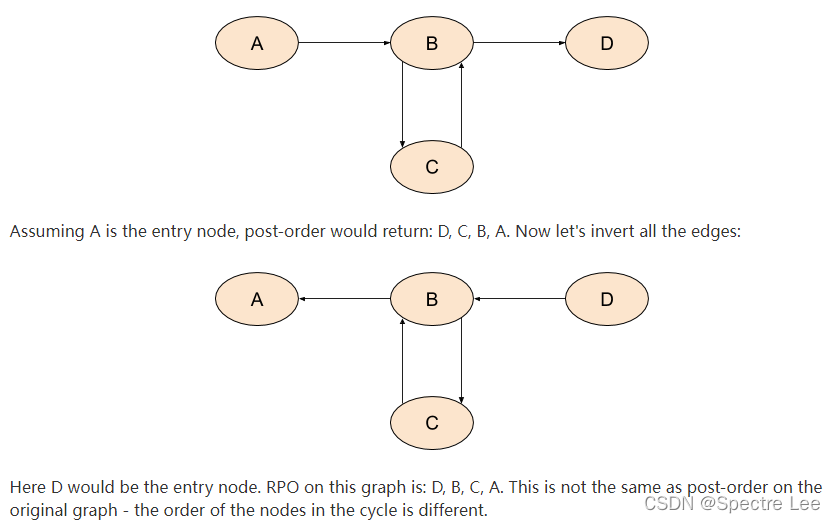
If I had to guess, I’d say that looking at the sample graph in this section, it makes some sense to examine B before C, because more of its successors were already visited. If we visit C before B, we don’t know much about successors yet because B wasn’t visited - and B is the only successor of C. But if we visit B before C, at least D (a successor of B in the original graph) was already visited.
按照顺序遍历，上面的图中B永远更 接近入口node~