强化学习导论(Reinforcement Learning: An Introduction)读书笔记四:动态规划
写在前面
~~~~~~~
由于专业学习的需要,最近开始学习强化学习的课程。目前看的书本是被誉为强化学习圣经的《Reinforcement Learning: An Introduction》,在学习过程中看到了两篇很好的笔记,强化学习导论(Reinforcement Learning: An Introduction)读书笔记(一):强化学习介绍.
强化学习导论(Reinforcement Learning: An Introduction)读书笔记(二):多臂赌博机(Multi-arm Bandits).
~~~~~~~
也用同样的风格写下第三章。
强化学习导论(Reinforcement Learning: An Introduction)读书笔记(三):有限马尔可夫决策过程.
~~~~~~~
但是由于水平有限,只能作为模仿,自我整理,向大佬致敬。这是第四章的读书笔记。
~~~~~~~
非常感谢强化学习系列(四):动态规划对于书中内容的整理,以及忆臻.文章,让我对动态规划有了更加深入的理解。
1.动态规划算法的核心
~~~~~~~
动态规划算法是为了在给定完整的环境模型的情况下,对马尔可夫决策过程MDP计算求解,得到最优策略的算法集合。其核心方法就是通过价值函数(value function)去寻求最优策略(optimal policy)。
~~~~~~~
在前一章我们得到了关于最优价值函数(optimal value function)
v
∗
v_*
v∗ 与
q
∗
q_*
q∗的方程:
v
∗
(
s
)
=
max
a
E
[
R
t
+
1
+
γ
v
∗
(
S
t
+
1
)
∣
S
t
=
s
,
A
t
=
a
]
=
max
a
∑
s
′
,
r
p
(
s
′
,
r
∣
s
,
a
)
[
r
+
γ
v
∗
(
s
′
)
]
\begin{aligned} v_*(s) &= \max_a\mathbb{E}[R_{t+1}+\gamma v_*(S_{t+1}) | S_t=s,A_t=a] \\ &= \max_a\sum_{s',r}p(s',r|s,a)[r+\gamma v_*(s')] \end{aligned}
v∗(s)=amaxE[Rt+1+γv∗(St+1)∣St=s,At=a]=amaxs′,r∑p(s′,r∣s,a)[r+γv∗(s′)]
q
∗
(
s
,
a
)
=
E
[
R
t
+
1
+
γ
max
a
′
q
∗
(
S
t
+
1
,
a
′
)
∣
S
t
=
s
,
A
t
=
a
]
=
∑
s
′
,
r
p
(
s
′
,
r
∣
s
,
a
)
[
r
+
γ
max
a
′
q
∗
(
s
′
,
a
′
)
]
,
\begin{aligned} q_*(s,a)& = \mathbb{E}[R_{t+1}+\gamma \max_{a'} q_*(S_{t+1},a') | S_t=s,A_t=a]\\ &=\sum_{s',r}p(s',r|s,a)[r+\gamma\max_{a'} q_*(s',a')], \end{aligned}
q∗(s,a)=E[Rt+1+γa′maxq∗(St+1,a′)∣St=s,At=a]=s′,r∑p(s′,r∣s,a)[r+γa′maxq∗(s′,a′)],
~~~~~~~
其中
s
∈
S
s\in\mathcal{S}
s∈S,
a
∈
A
(
s
)
a\in\mathcal{A}(s)
a∈A(s),以及
s
′
∈
S
+
s^\prime\in\mathcal{S^+}
s′∈S+。动态规划算法(Dynamic Programming) 就是将贝尔曼方程(Bellman equation) 改写为迭代更新的格式。
2. 策略价值评估
在DP中,对某种策略(policy) π \pi π的情况下,状态价值函数(state-value function) 的计算方式在MDP 过程中已经给出。针对于所有的 s ∈ S s\in\mathcal{S} s∈S:
v π ( s ) ≐ E π [ G t ∣ S t = s ] = E π [ R t + 1 + γ G t + 1 ∣ S t = s ] = E π [ R t + 1 + γ v π ( S t + 1 ) ∣ S t = s ] = ∑ a π ( a ∣ s ) ∑ s ′ , r p ( s ′ , r ∣ s , a ) [ r + γ v π ( s ′ ) ] \begin{aligned} v_\pi(s) & \doteq \mathbb{E_\pi}[G_t | S_t=s] \\ &= \mathbb{E_\pi}[R_{t+1} + \gamma G_{t+1} | S_t=s] \\ &= \mathbb{E_\pi}[R_{t+1}+\gamma v_\pi(S_{t+1}) | S_t=s] \\ &= \sum_a\pi(a|s)\sum_{s',r}p(s',r|s,a)[r+\gamma v_\pi(s')] \end{aligned} vπ(s)≐Eπ[Gt∣St=s]=Eπ[Rt+1+γGt+1∣St=s]=Eπ[Rt+1+γvπ(St+1)∣St=s]=a∑π(a∣s)s′,r∑p(s′,r∣s,a)[r+γvπ(s′)]
~~~~~~~
该方程是一个同时存在
∣
S
∣
|\mathcal{S}|
∣S∣个线性方程以及
∣
S
∣
|\mathcal{S}|
∣S∣个未知数的的线性方程组,其计算过程非常直白,但是计算量可能会非常大。因此,我们采用迭代的方式将价值函数进行更新。利用上述式子中的Bellman 方程 更新的规则为:
v
k
+
1
(
s
)
=
⋅
E
[
R
t
+
1
+
γ
v
k
(
S
t
+
1
)
∣
S
t
=
s
]
=
∑
a
π
(
a
∣
s
)
∑
s
′
,
r
p
(
s
′
,
r
∣
s
,
a
)
[
r
+
γ
v
k
(
s
′
)
]
,
\begin{aligned} v_{k+1}(s)& \overset{\cdot}{=}\mathbb{E}[R_{t+1}+\gamma v_k(S_{t+1}) | S_t=s] \\ &= \sum_{a}\pi(a|s)\sum_{s',r}p(s',r|s,a)[r+\gamma{v_k(s')}], \end{aligned}
vk+1(s)=⋅E[Rt+1+γvk(St+1)∣St=s]=a∑π(a∣s)s′,r∑p(s′,r∣s,a)[r+γvk(s′)],
~~~~~~~ 其中, s ∈ S s\in\mathcal{S} s∈S。随着 k k k值的不断变大, k → ∞ k\rightarrow\infty k→∞, { v k } \{v_k\} {vk}序列可以保证在广泛意义下收敛到 v π v_\pi vπ。该方法被称为 迭代策略评估 (iterative policy evaluation)
expected update: 状态 s s s的新的价值(new value) 是基于旧价值(old value) 的期望得到的,所以这种更新也被称为期望的更新。
2.1 两种迭代方式
两个数组: 两个数组是指在迭代过程中使用两个数组,一个用来存储旧的价值函数值,一个用来存储新的价值函数值。若第二数组被更新后,下一次更新继续覆盖第一个数组。该种更新方式就是整体得算价值函数,更新是全部的
s
s
s状态一起更新的。
一个数组: 一个数组的迭代就是,针对于任何一个状态
s
s
s,其状态价值更新后立刻覆盖旧的值。这样的计算收敛速度更快。
2.2 政策价值评估的算法
政策价值评估的算法流程图如下所示。其过程如下:

~~~~~~~ 需要注意的是,其他状态的初始值都是任意给定的,对于最终状态的价值,必须给0。
2.3 举例说明
~~~~~~~ 下图为一个4X4的矩阵,代表了一个gridword,其规则如下:
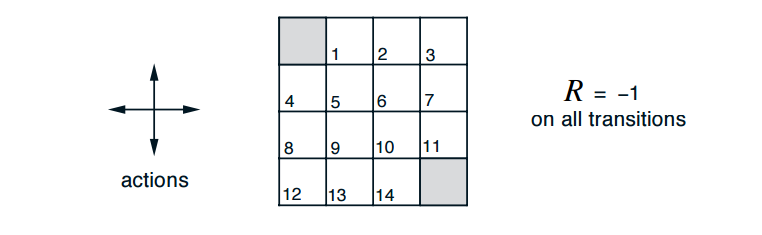
- 每个奖励的折扣因子 γ \gamma γ为1
- 格子1,2,3,…,14为非终止状态
- 两个灰色的格子为终止状态
- 到达非终止状态的奖励 (reward) 为 -1,终止状态奖励为 0
- 在非终止状态可以选择的动作为 A = { u p , d o w n , r i g h t , l e f t } \mathcal{A}=\{up, down, right, left\} A={up,down,right,left},四个动作的概率相同。
- 若执行动作后离开边界,下一个状态位置仍在原来保持不变。
基于这样的规则,可以迭代计算状态值来自知乎:叶强.

3.策略的改进与提升
3.1 如何提升策略
~~~~~~~
制定策略的目的是为了寻找最好的策略
π
∗
\pi_{*}
π∗,但是在刚刚开始时,由于我们对每个状态 (states) 的价值 (value) 并不了解,策略是随机制定的。在对策略进行评估 (Policy Evaluation) 后,才有改进策略的可能。
~~~~~~~
讨论这样一种情况,有一个新的策略
π
′
\pi'
π′,其和策略
π
\pi
π只在状态
s
s
s处不同,其余均一致。在状态
s
s
s下,动作价值函数的定义为:
q
π
(
s
,
a
)
≐
E
[
R
t
+
1
+
γ
v
π
(
S
t
+
1
)
∣
S
t
=
s
,
A
t
=
a
]
=
∑
s
′
,
r
p
(
s
′
,
r
∣
s
,
a
)
[
r
+
γ
v
π
(
s
′
)
]
\begin{aligned} q_\pi(s,a)& \doteq \mathbb{E}[R_{t+1}+\gamma v_\pi(S_{t+1}) | S_t=s,A_t=a] \\ &= \sum_{s',r}p(s',r|s,a)[r+\gamma v_\pi(s')] \end{aligned}
qπ(s,a)≐E[Rt+1+γvπ(St+1)∣St=s,At=a]=s′,r∑p(s′,r∣s,a)[r+γvπ(s′)]
~~~~~~~
假设新策略满足:
q
π
(
s
,
π
′
(
s
)
)
≥
v
π
(
s
)
q_\pi(s,\pi'(s)) \geq v_\pi(s)
qπ(s,π′(s))≥vπ(s)
~~~~~~~
那么策略
π
′
\pi'
π′ 必须与策略
π
\pi
π同样好或者比策略
π
\pi
π更好,即:
v
π
′
(
s
)
≥
v
π
(
s
)
v_\pi'(s) \geq v_\pi(s)
vπ′(s)≥vπ(s)
~~~~~~~
这样,我们就实现了我们的需求,我们的策略实现了提升 (policy improvement)
3.2 策略提升的证明
~~~~~~~ 策略提升理论的证明过程如下:
v
π
(
s
)
≤
q
π
(
s
,
π
′
(
s
)
)
=
E
[
R
t
+
1
+
γ
v
π
(
S
t
+
1
)
∣
S
t
=
s
,
A
t
=
π
′
(
s
)
]
=
E
π
′
[
R
t
+
1
+
γ
v
π
(
S
t
+
1
)
∣
S
t
=
s
]
≤
E
π
′
[
R
t
+
1
+
γ
q
π
(
S
t
+
1
,
π
′
(
S
t
+
1
)
)
∣
S
t
=
s
]
=
E
π
′
[
R
t
+
1
+
γ
E
π
′
[
R
t
+
2
+
γ
v
π
(
S
t
+
2
)
∣
S
t
+
1
,
A
t
=
π
′
(
s
+
1
)
]
∣
S
t
=
s
]
=
E
π
′
[
R
t
+
1
+
γ
R
t
+
2
+
γ
2
v
π
(
S
t
+
2
)
∣
S
t
=
s
]
≤
E
π
′
[
R
t
+
1
+
γ
R
t
+
2
+
γ
2
R
t
+
3
+
γ
3
v
π
(
S
t
+
3
)
∣
S
t
=
s
]
⋮
≤
E
π
′
[
R
t
+
1
+
γ
R
t
+
2
+
γ
2
R
t
+
3
+
γ
3
R
t
+
4
+
⋯
∣
S
t
=
s
]
=
v
π
′
(
s
)
\begin{aligned} v_\pi(s)& \leq q_\pi(s,\pi'(s))\\ &= \mathbb{E}[R_{t+1}+\gamma v_\pi(S_{t+1}) | S_t=s,A_t=\pi'(s)] & \\ &= \mathbb{E}_{\pi'}[R_{t+1}+\gamma v_\pi(S_{t+1}) | S_t=s] \\ & \leq\mathbb{E}_{\pi'}[R_{t+1}+\gamma q_\pi(S_{t+1},\pi'(S_{t+1})) | S_t=s] & \\ &= \mathbb{E}_{\pi'}[R_{t+1}+\gamma \mathbb{E}_{\pi'}[R_{t+2}+\gamma v_\pi(S_{t+2})| S_{t+1},A_t=\pi'(s+1) ] | S_t=s] \\ &= \mathbb{E}_{\pi'}[R_{t+1}+\gamma R_{t+2}+\gamma^2 v_\pi(S_{t+2}) | S_t=s] \\ & \leq\mathbb{E}_{\pi'}[R_{t+1}+\gamma R_{t+2}+\gamma^2 R_{t+3}+\gamma^3 v_\pi(S_{t+3}) | S_t=s] \\ & \vdots \\ & \leq \mathbb{E}_{\pi'}[R_{t+1}+\gamma R_{t+2}+\gamma^2R_{t+3}+\gamma^3R_{t+4}+\cdots | S_t=s] \\ &=v_{\pi'}(s) \end{aligned}
vπ(s)≤qπ(s,π′(s))=E[Rt+1+γvπ(St+1)∣St=s,At=π′(s)]=Eπ′[Rt+1+γvπ(St+1)∣St=s]≤Eπ′[Rt+1+γqπ(St+1,π′(St+1))∣St=s]=Eπ′[Rt+1+γEπ′[Rt+2+γvπ(St+2)∣St+1,At=π′(s+1)]∣St=s]=Eπ′[Rt+1+γRt+2+γ2vπ(St+2)∣St=s]≤Eπ′[Rt+1+γRt+2+γ2Rt+3+γ3vπ(St+3)∣St=s]⋮≤Eπ′[Rt+1+γRt+2+γ2Rt+3+γ3Rt+4+⋯∣St=s]=vπ′(s)
公式解读:
q
π
(
s
,
π
′
(
s
)
)
=
E
[
R
t
+
1
+
γ
v
π
(
S
t
+
1
)
∣
S
t
=
s
,
A
t
=
π
′
(
s
)
]
q_\pi(s,\pi'(s))= \mathbb{E}[R_{t+1}+\gamma v_\pi(S_{t+1}) | S_t=s,A_t=\pi'(s)]
qπ(s,π′(s))=E[Rt+1+γvπ(St+1)∣St=s,At=π′(s)]
~~~~~~~
这部分将价值函数展开,采用不等式:
q
π
(
s
,
π
′
(
s
)
)
≥
v
π
(
s
)
q_\pi(s,\pi'(s)) \geq v_\pi(s)
qπ(s,π′(s))≥vπ(s)。将
v
π
(
s
)
v_\pi(s)
vπ(s)替换为
q
π
(
s
,
π
′
(
s
)
)
q_\pi(s,\pi'(s))
qπ(s,π′(s)),之后对每个状态
s
s
s都进行替换,得到策略提升的证明结果!
4. 策略迭代
~~~~~~~
综合上面两部分讲,为了得到更好的策略,策略的评估 (Evaluation) 以及策略的提升 (improvement) 都非常重要。寻求一个最优策略意味着要反复利用这两点。
~~~~~~~
两者的反复组合就是策略迭代 (policy iteraction) 的过程。其变化过程可以表示为:
π
0
→
E
v
π
0
→
I
π
1
→
E
v
π
1
→
I
π
2
→
E
⋯
→
I
π
∗
→
E
v
∗
\pi_0 \overset{E}{\rightarrow} v_{\pi_0} \overset{I}{\rightarrow} \pi_1 \overset{E}{\rightarrow} v_{\pi_1} \overset{I}{\rightarrow} \pi_2 \overset{E}{\rightarrow} \cdots \overset{I}{\rightarrow} \pi_* \overset{E}{\rightarrow} v_{*}
π0→Evπ0→Iπ1→Evπ1→Iπ2→E⋯→Iπ∗→Ev∗
公式解读: 本质上来说,策略迭代包括了两个部分,第一部分是针对给的的策略
π
\pi
π,可以通过 Bellman 方程评估最优的价值函数,而通过上章内容,借助最优价值函数,我们可以对重新制定更好的策略
π
′
\pi'
π′…如此重复,就可以得到最优价值函数。
~~~~~~~
策略迭代的流程图 如下所示:

5. 价值迭代
~~~~~~~ 策略迭代的缺陷在于策略评估需要进行多次迭代。而我们其实是不需要等带价值函数 收敛的,对价值函数的迭代仅进行一次的迭代行为称为 价值迭代 (policy evaluation is stopped after just one sweep),价值迭代的示意图如下:

6.动态规划的扩展
原位动态规划(In-place dynamic programming)
~~~~~~~
直接原地更新下一个状态的v值,而不像同步迭代那样需要额外存储新的v值。在这种情况下,按何种次序更新状态价值有时候会比较有意义。
重要状态优先更新(Priortised Sweeping)
~~~~~~~
对于那些重要的状态先更新
写在最后
~~~~~~~ 关于这本《Reinforcement Learning: An Introduction》的英文原书,确实很难,自己看的也比较慢,希望可以继续坚持。希望能够和更多人一起交流!
链接: 这是《Reinforcement Learning: An Introduction》习题答案的链接,是一个博主自己写的。
链接: 这是《Reinforcement Learning: An Introduction》的代码示例,这个比较厉害.






















 1万+
1万+











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








