《剑指offer》之二叉搜索树(BST)与平衡二叉树(AVL树)专题
- 【前言】此文讲解BST和AVL,并配以剑指offer相关习题。
(一).二叉搜索树的查找,插入和删除操作
二叉搜索树又称为二叉查找树,二叉排序树(Binary Sort Tree),是满足以下条件的二叉树:1.左子树上的所有节点值均小于根节点值,2右子树上的所有节点值均不小于根节点值,3,左右子树也满足上述两个条件。(左小右大)
- 【查找】
//二叉树结构
private class TreeNode {
private int val;
private TreeNode leftChild;
private TreeNode rightChild;
private TreeNode parent;
public TreeNode(int val, TreeNode leftChild, TreeNode rightChild,
TreeNode parent) {
this.val = val;
this.leftChild = leftChild;
this.rightChild = rightChild;
this.parent = parent;
}
}//非递归查找方式
public TreeNode Search(TreeNode root,int key){
if(root==null){
return null;
}
TreeNode pNode = root;
while (pNode != null && pNode.val != key) {
if (key < pNode.val) {
pNode = pNode.leftChild;
} else {
pNode = pNode.rightChild;
}
}
return pNode;
} /**
* minElemNode: 获取二叉查找树中的最小关键字结点
*
* @return 二叉查找树的最小关键字结点
*
*
*/
public TreeNode minElemNode(TreeNode node) {
if (node == null) {
return null;
}
TreeNode pNode = node;
while (pNode.leftChild != null) {
pNode = pNode.leftChild;
}
return pNode;
}
/**
* maxElemNode: 获取二叉查找树中的最大关键字结点
*
* @return 二叉查找树的最大关键字结点
*
*
*/
public TreeNode maxElemNode(TreeNode node) {
if (node == null) {
return null ;
}
TreeNode pNode = node;
while (pNode.rightChild != null) {
pNode = pNode.rightChild;
}
return pNode;
} 【注意】:中序遍历二叉树得到的是递增序列,所以后继结点就是递增序列中该结点的下一位,分为三种情况:1.该结点有右子树,则右字数中最小值即为该结点后继结点 2.该结点无右子树且该结点是父节点的左子树,则该节点的父节点则为后继结点 3.该结点无右子树且该结点是父节点的右子树,则不断往父节点遍历。
/**
* successor: 获取给定结点在中序遍历顺序下的后继结点
*
* @param node
* 给定树中的结点
* @return 若该结点存在中序遍历顺序下的后继结点,则返回其后继结点;否则返回 null
* @throws Exception
*/
public TreeNode successor(TreeNode node) throws Exception {
if (node == null) {
return null;
}
// 若该结点的右子树不为空,则其后继结点就是右子树中的最小关键字结点
if (node.rightChild != null) {
return minElemNode(node.rightChild);
}
// 若该结点右子树为空
TreeNode parentNode = node.parent;
while (parentNode != null && node == parentNode.rightChild) {
node = parentNode;
parentNode = parentNode.parent;
}
return parentNode;
} - 【插入】
/**
* insert: 将给定关键字插入到二叉查找树中
*
* @param key
* 给定关键字
*/
public void insert(int key) {
TreeNode parentNode = null;
TreeNode newNode = new TreeNode(key, null, null, null);
TreeNode pNode = root;
if (root == null) {
root = newNode;
return;
}
while (pNode != null) {
parentNode = pNode;
if (key < pNode.key) {
pNode = pNode.leftChild;
} else if (key > pNode.key) {
pNode = pNode.rightChild;
} else {
// 树中已存在匹配给定关键字的结点,则什么都不做直接返回
return;
}
}
if (key < parentNode.key) {
parentNode.leftChild = newNode;
newNode.parent = parentNode;
} else {
parentNode.rightChild = newNode;
newNode.parent = parentNode;
}
} - 【删除给定的结点】
【注意】分为三种情况:1.删除结点是叶子结点,直接删除即可 2.删除结点仅有左或者右子树的结点,独子继承父业 3.删除结点左右子树都有结点,则删除该结点,并用该后继结点取代该结点 。
/**
* delete: 从二叉查找树中删除给定的结点.
*
* @param pNode
* 要删除的结点
*
* 前置条件: 给定结点在二叉查找树中已经存在
* @throws Exception
*/
private void delete(TreeNode pNode) throws Exception {
if (pNode == null) {
return;
}
if (pNode.leftChild == null && pNode.rightChild == null) { // 该结点既无左孩子结点,也无右孩子结点
TreeNode parentNode = pNode.parent;
if (pNode == parentNode.leftChild) {
parentNode.leftChild = null;
} else {
parentNode.rightChild = null;
}
return;
}
if (pNode.leftChild == null && pNode.rightChild != null) { // 该结点左孩子结点为空,右孩子结点非空
TreeNode parentNode = pNode.parent;
if (pNode == parentNode.leftChild) {
parentNode.leftChild = pNode.rightChild;
pNode.rightChild.parent = parentNode;
} else {
parentNode.rightChild = pNode.rightChild;
pNode.rightChild.parent = parentNode;
}
return;
}
if (pNode.leftChild != null && pNode.rightChild == null) { // 该结点左孩子结点非空,右孩子结点为空
TreeNode parentNode = pNode.parent;
if (pNode == parentNode.leftChild) {
parentNode.leftChild = pNode.leftChild;
pNode.rightChild.parent = parentNode;
} else {
parentNode.rightChild = pNode.leftChild;
pNode.rightChild.parent = parentNode;
}
return;
}
// 该结点左右孩子结点均非空,则删除该结点,并用该后继结点取代该结点
TreeNode successorNode = successor(pNode);
delete(successorNode);
pNode.key = successorNode.key;
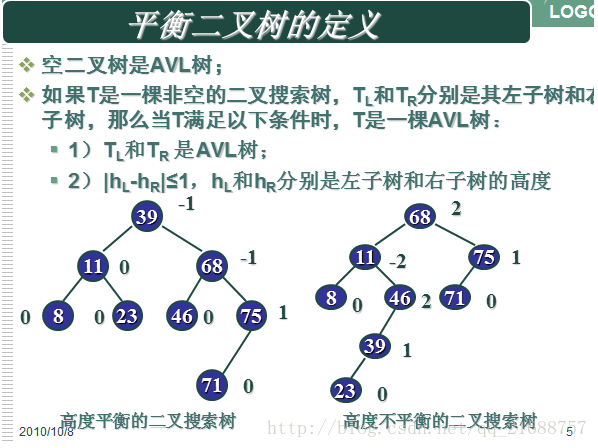
} (二).平衡二叉树(AVL树)
平衡二叉树是一种二叉搜索树,其中每一个节点的左子树和右子树的高度差至多等于1。将二叉树左子树的深度减去右子树的深度值称为平衡因子BF,那么平衡二叉树的所有结点的平衡因子只可能是-1,0和1。只要二叉树上有一个结点的平衡因子的绝对值大于1,则该二叉树就是不平衡的。
(三).《剑指offer》上二叉搜索树(BST)与平衡二叉树(AVL树)的题目
1.二叉搜索树的后序遍历序列
【题目】输入一个整数数组,判断该数组是不是某二叉搜索树的后序遍历的结果。如果是则输出Yes,否则输出No。假设输入的数组的任意两个数字都互不相同。
后序遍历的顺序:左右根
二叉搜索树左子树的值小于结点值,右子树的值大于结点值
最后一个为根结点,最重要是找到左字数和右字数的分界
举例:{5,7,6,9,11,10,8}
public class Solution {
/**
1.后序遍历的顺序:左右根
2.二叉搜索树左子树的值小于结点值,右子树的值大于结点值
3.最后一个为根结点,最重要是找到左字数和右字数的分界
4.举例:{5,7,6,9,11,10,8}
*/
public boolean VerifySquenceOfBST(int [] sequence) {
if(sequence.length==0){
return false;
}
if(sequence.length==1){
return true;
}
return ju(sequence,0,sequence.length-1);
}
public boolean ju(int[] a,int start,int end){
//跳出循环的条件
if(start>=end){
return true;
}
//根结点在最后一个,从后面找,找到右结点的第一个数
int i = end;
while(i>start && a[i-1]>a[end]){
i--;
}
//满足左子树所有值小于根结点
for(int j=start;j<i-1;j++){
if(a[j]>a[end]){
return false;
}
}
//对左右子树递归
return ju(a,start,i-1)&&ju(a,i,end-1);
}
}2.二叉搜索树的第k个结点
【题目】给定一颗二叉搜索树,请找出其中的第k大的结点。例如, 5 / \ 3 7 /\ /\ 2 4 6 8 中,按结点数值大小顺序第三个结点的值为4。
- 二叉搜索树中序遍历序列化之后为递增数列,对称中序遍历后为递减数列
- 引入计数器 count
/*
public class TreeNode {
int val = 0;
TreeNode left = null;
TreeNode right = null;
public TreeNode(int val) {
this.val = val;
}
}
*/
/**
1.二叉搜索树中序遍历序列化之后为递增数列,对称中序遍历后为递减数列
2.引入计数器 count
**/
public class Solution {
int count = 0;
TreeNode KthNode(TreeNode pRoot, int k)
{
if(pRoot == null || k==0){
return null;
}
TreeNode t = KthNode(pRoot.left,k);
//类似拦截,一旦返回非空就一直返回该结点
if(t!=null){
return t;
}
//先对count加一再和k比较
if(++count<k){
return KthNode(pRoot.right,k);
}else if(count == k){
return pRoot;
}
return null;
}
}3.二叉搜索树与双向链表
【题目】输入一棵二叉搜索树,将该二叉搜索树转换成一个排序的双向链表。要求不能创建任何新的结点,只能调整树中结点指针的指向。
/**
public class TreeNode {
int val = 0;
TreeNode left = null;
TreeNode right = null;
public TreeNode(int val) {
this.val = val;
}
}
*/
public class Solution {
//二叉搜索树中序遍历递增排序, 根 左 右
//双向链表的左边头结点和右边头结点
TreeNode leftNode = null;
TreeNode rightNode = null;
public TreeNode Convert(TreeNode pRootOfTree) {
//递归调用叶子节点的左右节点时返回null
if(pRootOfTree == null){
return null;
}
Convert(pRootOfTree.left);
//第一次遍历左子树里的最小值,把节点赋值给左边头结点和右边头结点
if(rightNode == null){
leftNode = rightNode = pRootOfTree;
}else{
//把遍历到的节点放到rightNode后边,把rightNode往后移一位
rightNode.right = pRootOfTree;
pRootOfTree.left = rightNode;
rightNode = pRootOfTree;
}
Convert(pRootOfTree.right);
return leftNode;
}4.平衡二叉树
【题目】 输入一棵二叉树,判断该二叉树是否是平衡二叉树。
- 平衡二叉树平衡因子不能大于|1|,所以关键是通过后序遍历得到左右子树的深度
public class Solution {
public boolean IsBalanced_Solution(TreeNode root) {
return isB(root)>=0;
}
private int isB(TreeNode root){
//递归循环跳出的条件
if(root == null){
return 0;
}
//后序遍历平衡二叉树,左 右 根,返回该结点的左右子树深度
int l = isB(root.left);
int r = isB(root.right);
//这句意义是一旦平衡因子超过1,不用比较,直接退出-1
if(l<0 || r<0){
return -1;
}
if(Math.abs(r-l)>1){
return -1;
}
//遍历一个结点,左右子树深度有一个加一
return r>l?r+1:l+1;
}
}






















 576
576

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








