节点定位方法
1. 节点定位的计算
在 WSNs 的定位中,未知节点通过一定的技术和方法能够获得定位自身所需的坐标、角度或距离信息,从而利用节点位置的计算方法计算自身位置。下面我们将介绍几种较为典型的位置计算方法:三边测量法、三角测量法、极大似然估计法、最小二乘法等。
1.1 三边测量法
在二维空间位置计算中,当未知节点获得三个 BS 节点的位置和距离信息时,可通过三边测量方法计算 MS 位置。
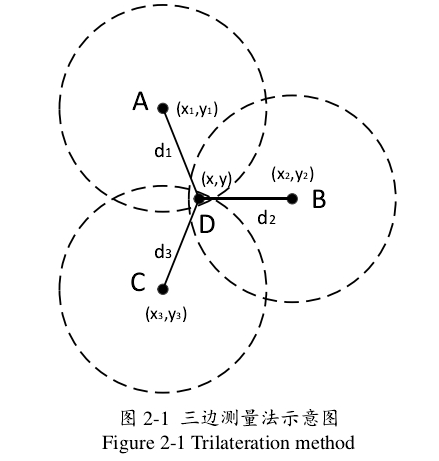
如图所示,未知节点 D,其坐标
(
x
,
y
)
(x,y)
(x,y) 未知;通信半径内有三个 BS 节点 A、B、C,三个 BS 节点的位置已知,分别为
(
x
1
,
y
1
)
,
(
x
2
,
y
2
)
,
(
x
3
,
y
3
)
(x_1,y_1),(x_2,y_2),(x_3,y_3)
(x1,y1),(x2,y2),(x3,y3),通过一定的方法估测出未知节点与 BS 节点之间的距离为
d
1
,
d
2
,
d
3
d_1,d_2,d_3
d1,d2,d3。由此可得
(
x
−
x
i
)
2
+
(
y
−
y
i
)
2
=
d
i
2
⇓
x
2
+
y
2
+
x
i
2
+
y
i
2
−
2
x
i
x
−
2
y
i
y
=
d
i
2
,
i
=
1
,
2
,
3.
(x-x_i)^2+(y-y_i)^2 = d_i^2 \\ \Downarrow \\ x^2+y^2+x_i^2+y_i^2-2x_ix-2y_iy = d_i^2,\quad i=1,2,3.
(x−xi)2+(y−yi)2=di2⇓x2+y2+xi2+yi2−2xix−2yiy=di2,i=1,2,3.
未知参数除了
x
,
y
x,y
x,y 还有
x
2
+
y
2
x^2+y^2
x2+y2,于是采用高斯消元法可得
d
3
2
−
d
1
2
=
2
(
x
1
−
x
3
)
x
+
2
(
y
1
−
y
3
)
y
+
x
3
2
−
x
1
2
+
y
3
2
−
y
1
2
d
3
2
−
d
2
2
=
2
(
x
2
−
x
3
)
x
+
2
(
y
2
−
y
3
)
y
+
x
3
2
−
x
2
2
+
y
3
2
−
y
2
2
\begin{aligned} d_3^2-d_1^2 &= 2(x_1-x_3)x+2(y_1-y_3)y+x_3^2-x_1^2+y_3^2-y_1^2 \\ d_3^2-d_2^2 &= 2(x_2-x_3)x+2(y_2-y_3)y+x_3^2-x_2^2+y_3^2-y_2^2 \end{aligned}
d32−d12d32−d22=2(x1−x3)x+2(y1−y3)y+x32−x12+y32−y12=2(x2−x3)x+2(y2−y3)y+x32−x22+y32−y22
现在转化为只含有两个未知数得方程组,因此可利用求逆得到解。
[
d
3
2
−
d
1
2
−
x
3
2
+
x
1
2
−
y
3
2
+
y
1
2
d
3
2
−
d
2
2
−
x
3
2
+
x
2
2
−
y
3
2
+
y
2
2
]
=
[
2
(
x
1
−
x
3
)
2
(
y
1
−
y
3
)
2
(
x
2
−
x
3
)
2
(
y
2
−
y
3
)
]
[
x
y
]
\begin{bmatrix} d_3^2-d_1^2-x_3^2+x_1^2-y_3^2+y_1^2 \\ d_3^2-d_2^2-x_3^2+x_2^2-y_3^2+y_2^2 \end{bmatrix} = \begin{bmatrix} 2(x_1-x_3)&2(y_1-y_3) \\ 2(x_2-x_3)&2(y_2-y_3) \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix}
[d32−d12−x32+x12−y32+y12d32−d22−x32+x22−y32+y22]=[2(x1−x3)2(x2−x3)2(y1−y3)2(y2−y3)][xy]
1.2 三角测量法
三角测量法利用 BS 节点与未知节点 MS 之间的角度信息,通过几何关系列出方程组,从而转化为三边测量计算方法的问题。

三角测量术常用到基于 AOA 方法的测距中, 它根据三个已知坐标的节点到未知节点的相对角度来确定节点坐标。三个 BS 节点 A、B、C 坐标分别为 ( x 1 , y 1 ) , ( x 2 , y 2 ) , ( x 3 , y 3 ) (x_1,y_1),(x_2,y_2),(x_3,y_3) (x1,y1),(x2,y2),(x3,y3),假设节点 D 的坐标为 ( x , y ) (x,y) (x,y),如图所示。
未知节点 D 到节点 A、B、C 之间的夹角分别为 ∠ A D B , ∠ A D C , ∠ B D C ∠ADB,∠ADC,∠BDC ∠ADB,∠ADC,∠BDC 已知。
通过节点 A、C 的坐标信息和角度
∠
A
D
C
\angle ADC
∠ADC 可唯一确定以
O
1
O_1
O1 为圆心,
d
1
d_1
d1 为半径的圆。则圆心为
(
x
O
1
,
y
O
1
)
(x_{O1},y_{O1})
(xO1,yO1),设
α
=
∠
A
O
1
C
=
2
(
18
0
∘
−
∠
A
D
C
)
\alpha=\angle AO_1C = 2(180^{\circ}-\angle ADC)
α=∠AO1C=2(180∘−∠ADC)。存在下列公式:
(
x
O
1
−
x
1
)
2
+
(
y
O
1
−
y
1
)
2
=
d
1
2
(
x
O
1
−
x
3
)
2
+
(
y
O
1
−
y
3
)
2
=
d
1
2
(
x
1
−
x
3
)
2
+
(
y
1
−
y
3
)
2
=
2
d
1
2
−
2
d
1
2
cos
α
\begin{aligned} (x_{O1}-x_1)^2+(y_{O1}-y_1)^2 &= d_1^2 \\ (x_{O1}-x_3)^2+(y_{O1}-y_3)^2 &= d_1^2 \\ (x_{1}-x_3)^2+(y_{1}-y_3)^2 &= 2d_1^2-2d_1^2\cos \alpha \end{aligned}
(xO1−x1)2+(yO1−y1)2(xO1−x3)2+(yO1−y3)2(x1−x3)2+(y1−y3)2=d12=d12=2d12−2d12cosα
由以上三式能够确定圆心
O
1
O_1
O1 的坐标和半径
d
1
2
=
(
x
1
−
x
3
)
2
+
(
y
1
−
y
3
)
2
2
(
1
−
cos
α
)
d_1^2 = \frac{(x_{1}-x_3)^2+(y_{1}-y_3)^2}{2(1-\cos \alpha)}
d12=2(1−cosα)(x1−x3)2+(y1−y3)2
同理可对 A、B、D 和 B、C、D 分别确定相应的圆心和半径,最后利用三边测量确定 D 的坐标。
1.3 极大似然估计法
该方法所运用的是求解最小误差点的原理,即存在一个点使得所有方程的误差最小。在极大似然估计法中,求解的是距离误差最小点。

如图所示,未知节点的通信范围内有
n
n
n 个 BS,且已知所有 BS 节点坐标,分别为
(
x
1
,
y
1
)
,
⋯
 
,
(
x
n
,
y
n
)
(x_1,y_1),\cdots,(x_n,y_n)
(x1,y1),⋯,(xn,yn)。通过某种方法获得了与各 BS 节点之间的距离
d
1
,
d
2
,
⋯
 
,
d
n
d_1,d_2,\cdots,d_n
d1,d2,⋯,dn。假设未知节点 A 的坐标为
(
x
,
y
)
(x,y)
(x,y)。由此可知
(
x
1
−
x
)
2
+
(
y
1
−
y
)
2
=
d
1
2
(
x
2
−
x
)
2
+
(
y
2
−
y
)
2
=
d
2
2
⋮
(
x
n
−
x
)
2
+
(
y
n
−
y
)
2
=
d
n
2
\begin{aligned} (x_{1}-x)^2+(y_{1}-y)^2 &= d_1^2 \\ (x_{2}-x)^2+(y_{2}-y)^2 &= d_2^2 \\ \vdots \\ (x_{n}-x)^2+(y_{n}-y)^2 &= d_n^2 \end{aligned}
(x1−x)2+(y1−y)2(x2−x)2+(y2−y)2⋮(xn−x)2+(yn−y)2=d12=d22=dn2
将方程组中的前
n
−
1
n-1
n−1 个方程减去第
n
n
n 个方程得
x
1
2
−
x
n
2
+
y
1
2
−
y
n
2
−
d
1
2
+
d
n
2
=
2
(
x
1
−
x
n
)
x
+
2
(
y
1
−
y
n
)
y
x
2
2
−
x
n
2
+
y
2
2
−
y
n
2
−
d
2
2
+
d
n
2
=
2
(
x
2
−
x
n
)
x
+
2
(
y
2
−
y
n
)
y
⋮
x
n
−
1
2
−
x
n
2
+
y
n
−
1
2
−
y
n
2
−
d
n
−
1
2
+
d
n
2
=
2
(
x
n
−
1
−
x
n
)
x
+
2
(
y
n
−
1
−
y
n
)
y
\begin{aligned} x_1^2-x_n^2+y_1^2-y_n^2-d_1^2+d_n^2 &= 2(x_1-x_n)x+2(y_1-y_n)y \\ x_2^2-x_n^2+y_2^2-y_n^2-d_2^2+d_n^2 &= 2(x_2-x_n)x+2(y_2-y_n)y \\ \vdots \\ x_{n-1}^2-x_n^2+y_{n-1}^2-y_n^2-d_{n-1}^2+d_n^2 &= 2(x_{n-1}-x_n)x+2(y_{n-1}-y_n)y \end{aligned}
x12−xn2+y12−yn2−d12+dn2x22−xn2+y22−yn2−d22+dn2⋮xn−12−xn2+yn−12−yn2−dn−12+dn2=2(x1−xn)x+2(y1−yn)y=2(x2−xn)x+2(y2−yn)y=2(xn−1−xn)x+2(yn−1−yn)y
即
[
x
1
2
−
x
n
2
+
y
1
2
−
y
n
2
−
d
1
2
+
d
n
2
x
2
2
−
x
n
2
+
y
2
2
−
y
n
2
−
d
2
2
+
d
n
2
⋮
x
n
−
1
2
−
x
n
2
+
y
n
−
1
2
−
y
n
2
−
d
n
−
1
2
+
d
n
2
]
=
[
2
(
x
1
−
x
n
)
2
(
y
1
−
y
n
)
2
(
x
2
−
x
n
)
2
(
y
2
−
y
n
)
⋮
2
(
x
n
−
1
−
x
n
)
2
(
y
n
−
1
−
y
n
)
]
[
x
y
]
\begin{bmatrix} x_1^2-x_n^2+y_1^2-y_n^2-d_1^2+d_n^2 \\ x_2^2-x_n^2+y_2^2-y_n^2-d_2^2+d_n^2 \\ \vdots \\ x_{n-1}^2-x_n^2+y_{n-1}^2-y_n^2-d_{n-1}^2+d_n^2 \end{bmatrix} = \begin{bmatrix} 2(x_1-x_n)&2(y_1-y_n) \\ 2(x_2-x_n)&2(y_2-y_n) \\ \vdots \\ 2(x_{n-1}-x_n)&2(y_{n-1}-y_n) \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix}
⎣⎢⎢⎢⎡x12−xn2+y12−yn2−d12+dn2x22−xn2+y22−yn2−d22+dn2⋮xn−12−xn2+yn−12−yn2−dn−12+dn2⎦⎥⎥⎥⎤=⎣⎢⎢⎢⎡2(x1−xn)2(x2−xn)⋮2(xn−1−xn)2(y1−yn)2(y2−yn)2(yn−1−yn)⎦⎥⎥⎥⎤[xy]
因此得到
D
=
K
X
D = KX
D=KX。此时利用 LS 来解。


























 1881
1881

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








