本文详细介绍了无线传感器网络中节点定位的三种常见方法：三边测距法、三角测距法和极大似然估计法。三边测距法基于距离信息，通过建立方程组求解；三角测距法利用角度和外接圆计算；极大似然估计法则结合多个信标节点的距离信息进行坐标估算。这些方法对于无线网络监控和目标追踪等应用至关重要。
计算节点位置的基本方法
在传感器节点定位过程中，通常根据未知节点（被监测节点）相对相邻信标节点的距离、角度进行计算位置。通常采用三边测距法、三角测距法或极大似然估计法进行计算。
三边测距法(Trilateration)
三边测距法的原理如下，已知未知节点D
(
x
,
y
)
(x, y)
(x,y)与相邻的三个信标节点
A
(
x
1
,
y
1
)
、
B
(
x
2
,
y
2
)
、
C
(
x
3
,
y
3
)
A(x_1, y_1)、B(x_2, y_2)、C(x_3, y_3)
A(x1,y1)、B(x2,y2)、C(x3,y3)间的距离分别为
d
a
、
d
b
、
d
c
d_a、d_b、d_c
da、db、dc，其示意图如下所示：
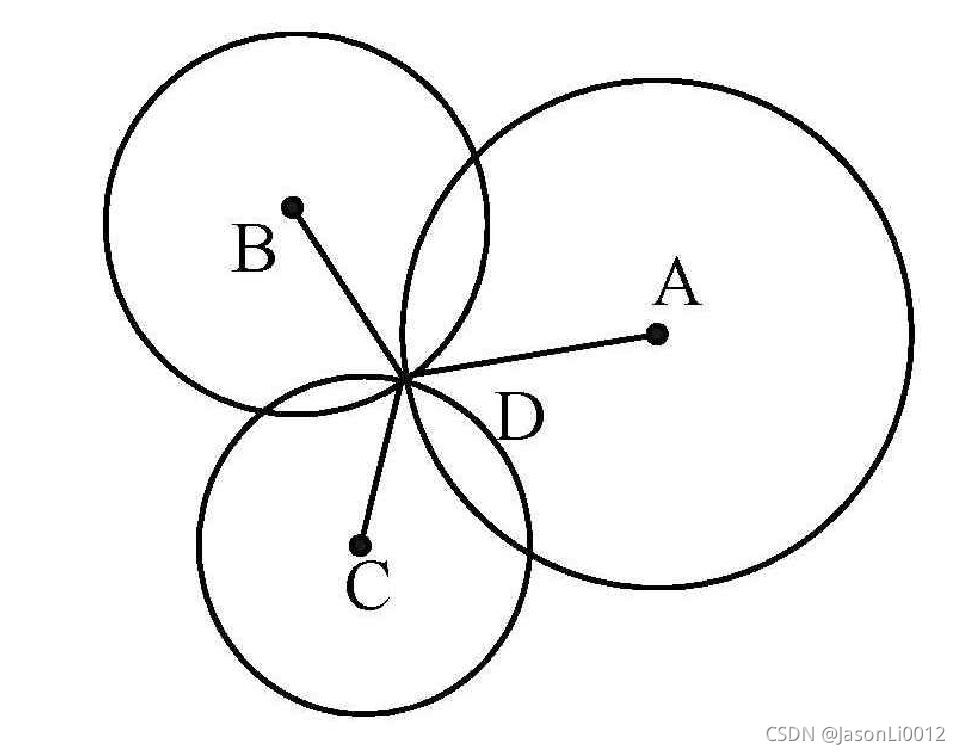
根据距离公式可罗列如下方程式：
{
(
x
a
−
x
)
2
+
(
y
a
−
y
)
2
=
d
a
(
x
b
−
x
)
2
+
(
y
b
−
y
)
2
=
d
b
(
x
c
−
x
)
2
+
(
y
c
−
y
)
2
=
d
c
\begin{cases} \sqrt{(x_a-x)^2 + (y_a-y)^2} = d_a \\ \sqrt{(x_b-x)^2 + (y_b-y)^2} = d_b \\ \sqrt{(x_c-x)^2 + (y_c-y)^2} = d_c \\ \end{cases}
⎩⎪⎨⎪⎧(xa−x)2+(ya−y)2=da(xb−x)2+(yb−y)2=db(xc−x)2+(yc−y)2=dc
求得结果如下：
[
x
y
]
=
[
2
(
x
a
−
x
c
)
2
(
y
a
−
y
c
)
2
(
x
b
−
x
c
)
2
(
y
b
−
y
c
)
]
−
1
[
x
a
2
−
x
c
2
+
y
a
2
−
y
c
2
+
d
c
2
−
d
a
2
x
b
2
−
x
c
2
+
y
b
2
−
y
c
2
+
d
c
2
−
d
b
2
]
\begin{bmatrix}x \\ y\end{bmatrix} = \begin{bmatrix} 2(x_a-x_c) & 2(y_a-y_c) \\ 2(x_b-x_c) & 2(y_b-y_c) \\ \end{bmatrix}^{-1} \begin{bmatrix} x_a^2 - x_c^2 + y_a^2 - y_c^2 + d_c^2 - d_a^2 \\ x_b^2 - x_c^2 + y_b^2 - y_c^2 + d_c^2 - d_b^2 \\ \end{bmatrix}
[xy]=[2(xa−xc)2(xb−xc)2(ya−yc)2(yb−yc)]−1[xa2−xc2+ya2−yc2+dc2−da2xb2−xc2+yb2−yc2+dc2−db2]
三角测距法(Triangulation)
三角测距法的原理如下，已知未知节点O ( x , y ) (x, y) (x,y)与相邻的三个信标节点 A ( x 1 , y 1 ) 、 B ( x 2 , y 2 ) 、 C ( x 3 , y 3 ) A(x_1, y_1)、B(x_2, y_2)、C(x_3, y_3) A(x1,y1)、B(x2,y2)、C(x3,y3)之间的夹角分别为 ∠ A O C 、 ∠ A O B 、 ∠ B O C ∠AOC、∠AOB、∠BOC ∠AOC、∠AOB、∠BOC，可唯一确定 △ A O B \triangle AOB △AOB、 △ A O C \triangle AOC △AOC、 △ B O C \triangle BOC △BOC的外接圆 O 1 、 O 2 、 O 3 O_1、O_2、O_3 O1、O2、O3。
其示意图如下所示：
为确定外接圆圆心坐标
O
1
(
x
O
1
,
y
O
1
)
O_1(x_{O_1}, y_{O_1})
O1(xO1,yO1)及其半径
r
1
r_1
r1，根据余弦公式、距离公式可罗列如下方程式：
{
(
x
O
1
−
x
1
)
2
+
(
y
O
1
−
y
1
)
2
=
r
1
(
x
O
1
−
x
2
)
2
+
(
y
O
1
−
y
2
)
2
=
r
1
(
x
1
−
x
2
)
2
+
(
y
1
−
y
2
)
2
=
2
r
1
2
−
2
r
1
2
⋅
cos
A
O
1
B
∠
A
O
1
B
=
2
π
−
∠
A
O
B
\begin{cases} \sqrt{(x_{O_1}-x_1)^2 + (y_{O_1}-y_1)^2} = r_1 \\ \sqrt{(x_{O_1}-x_2)^2 + (y_{O_1}-y_2)^2} = r_1 \\ (x_1 - x_2)^2 + (y_1 - y_2)^2 = 2r_1^2 - 2r_1^2\cdot\cos{AO_1B} \\ ∠AO_1B = 2\pi - ∠AOB \end{cases}
⎩⎪⎪⎪⎨⎪⎪⎪⎧(xO1−x1)2+(yO1−y1)2=r1(xO1−x2)2+(yO1−y2)2=r1(x1−x2)2+(y1−y2)2=2r12−2r12⋅cosAO1B∠AO1B=2π−∠AOB
同理，对于外接圆圆心坐标
O
2
(
x
O
2
,
y
O
2
)
、
O
3
(
x
O
3
,
y
O
3
)
O_2(x_{O_2}, y_{O_2})、O_3(x_{O_3}, y_{O_3})
O2(xO2,yO2)、O3(xO3,yO3)及其半径
r
2
、
r
3
r_2、r_3
r2、r3，可以罗列类似方程求出。最后，再利用三边测距法即可计算处节点
O
(
x
,
y
)
O(x, y)
O(x,y)的坐标。
{
(
x
O
1
−
x
)
2
+
(
y
O
1
−
y
)
2
=
r
1
(
x
O
2
−
x
)
2
+
(
y
O
2
−
y
)
2
=
r
2
(
x
O
3
−
x
)
2
+
(
y
O
3
−
y
)
2
=
r
3
\begin{cases} \sqrt{(x_{O_1}-x)^2 + (y_{O_1}-y)^2} = r_1 \\ \sqrt{(x_{O_2}-x)^2 + (y_{O_2}-y)^2} = r_2 \\ \sqrt{(x_{O_3}-x)^2 + (y_{O_3}-y)^2} = r_3 \\ \end{cases}
⎩⎪⎨⎪⎧(xO1−x)2+(yO1−y)2=r1(xO2−x)2+(yO2−y)2=r2(xO3−x)2+(yO3−y)2=r3
求得结果如下：
[
x
y
]
=
[
2
(
x
O
1
−
x
O
3
)
2
(
y
O
1
−
y
O
3
)
2
(
x
O
2
−
x
O
3
)
2
(
y
O
2
−
y
O
3
)
]
−
1
[
x
O
1
2
−
x
O
3
2
+
y
O
1
2
−
y
O
3
2
+
r
3
2
−
r
1
2
x
O
2
2
−
x
O
3
2
+
y
O
2
2
−
y
O
3
2
+
r
3
2
−
r
2
2
]
\begin{bmatrix}x \\ y\end{bmatrix} = \begin{bmatrix} 2(x_{O_1}-x_{O_3}) & 2(y_{O_1}-y_{O_3}) \\ 2(x_{O_2}-x_{O_3}) & 2(y_{O_2}-y_{O_3}) \\ \end{bmatrix}^{-1} \begin{bmatrix} x_{O_1}^2 - x_{O_3}^2 + y_{O_1}^2 - y_{O_3}^2 + r_3^2 - r_1^2 \\ x_{O_2}^2 - x_{O_3}^2 + y_{O_2}^2 - y_{O_3}^2 + r_3^2 - r_2^2 \\ \end{bmatrix}
[xy]=[2(xO1−xO3)2(xO2−xO3)2(yO1−yO3)2(yO2−yO3)]−1[xO12−xO32+yO12−yO32+r32−r12xO22−xO32+yO22−yO32+r32−r22]
极大似然估计法(Maximum Likelihood Estimation)
极大似然估计法原理如下，已知未知节点 D ( x , y ) D(x, y) D(x,y)附件存在n个信标节点，其坐标分别为 ( x 1 , y 1 ) 、 ( x 2 , y 2 ) 、 ( x 3 , y 3 ) … … ( x n , y n ) (x_1, y_1)、(x_2, y_2)、(x_3, y_3)……(x_n, y_n) (x1,y1)、(x2,y2)、(x3,y3)……(xn,yn)且各信标节点到未知节点的距离分别为 d 1 、 d 2 、 d 3 … … d n d_1、d_2、d_3……d_n d1、d2、d3……dn。
其示意图如下所示：
根据距离公式，可以罗列出如下方程式：
{
(
x
1
−
x
)
2
+
(
y
1
−
y
)
2
=
d
1
2
(
x
2
−
x
)
2
+
(
y
2
−
y
)
2
=
d
2
2
…
…
(
x
n
−
x
)
2
+
(
y
n
−
y
)
2
=
d
n
2
\begin{cases} (x_1 - x)^2 + (y_1 - y)^2 = d_1^2\\ (x_2 - x)^2 + (y_2 - y)^2 = d_2^2\\ ……\\ (x_n - x)^2 + (y_n - y)^2 = d_n^2 \end{cases}
⎩⎪⎪⎪⎨⎪⎪⎪⎧(x1−x)2+(y1−y)2=d12(x2−x)2+(y2−y)2=d22……(xn−x)2+(yn−y)2=dn2
对上述方程式，分别用每一个方程减去最后一个方程，可得到如下形式的方程式：
{
2
(
x
1
−
x
n
)
x
+
2
(
y
1
−
y
n
)
y
=
x
1
2
−
x
n
2
+
y
1
2
−
y
n
2
−
d
1
2
+
d
n
2
2
(
x
2
−
x
n
)
x
+
2
(
y
2
−
y
n
)
y
=
x
2
2
−
x
n
2
+
y
2
2
−
y
n
2
−
d
2
2
+
d
n
2
…
…
2
(
x
n
−
1
−
x
n
)
x
+
2
(
y
n
−
1
−
y
n
)
y
=
x
n
−
1
2
−
x
n
2
+
y
n
−
1
2
−
y
n
2
−
d
n
−
1
2
+
d
n
2
\begin{cases} 2(x_1 - x_n)x + 2(y_1 - y_n)y = x_1^2 - x_n^2 + y_1^2 - y_n^2 - d_1^2 + d_n^2\\ 2(x_2 - x_n)x + 2(y_2 - y_n)y = x_2^2 - x_n^2 + y_2^2 - y_n^2 - d_2^2 + d_n^2\\ ……\\ 2(x_{n-1} - x_n)x + 2(y_{n-1} - y_n)y = x_{n-1}^2 - x_n^2 + y_{n-1}^2 - y_n^2 - d_{n-1}^2 + d_n^2\\ \end{cases}
⎩⎪⎪⎪⎨⎪⎪⎪⎧2(x1−xn)x+2(y1−yn)y=x12−xn2+y12−yn2−d12+dn22(x2−xn)x+2(y2−yn)y=x22−xn2+y22−yn2−d22+dn2……2(xn−1−xn)x+2(yn−1−yn)y=xn−12−xn2+yn−12−yn2−dn−12+dn2
将方程式转换为
A
X
=
b
AX=b
AX=b形式，则：
A
=
[
2
(
x
1
−
x
n
)
2
(
y
1
−
y
n
)
2
(
x
2
−
x
n
)
2
(
y
2
−
y
n
)
…
…
2
(
x
n
−
1
−
x
n
)
2
(
y
n
−
1
−
y
n
)
]
，
b
=
[
x
1
2
−
x
n
2
+
y
1
2
−
y
n
2
−
d
1
2
+
d
n
2
x
2
2
−
x
n
2
+
y
2
2
−
y
n
2
−
d
2
2
+
d
n
2
…
…
x
n
−
1
2
−
x
n
2
+
y
n
−
1
2
−
y
n
2
−
d
n
−
1
2
+
d
n
2
]
，
X
=
[
x
y
]
A = \begin{bmatrix} 2(x_1 - x_n) & 2(y_1 - y_n) \\ 2(x_2 - x_n) & 2(y_2 - y_n) \\ …&…\\ 2(x_{n-1} - x_n) & 2(y_{n-1} - y_n) \end{bmatrix}，b = \begin{bmatrix} x_1^2 - x_n^2 + y_1^2 - y_n^2 - d_1^2 + d_n^2 \\ x_2^2 - x_n^2 + y_2^2 - y_n^2 - d_2^2 + d_n^2 \\ ……\\ x_{n-1}^2 - x_n^2 + y_{n-1}^2 - y_n^2 - d_{n-1}^2 + d_n^2 \end{bmatrix}，X = \begin{bmatrix} x \\ y \end{bmatrix}
A=⎣⎢⎢⎡2(x1−xn)2(x2−xn)…2(xn−1−xn)2(y1−yn)2(y2−yn)…2(yn−1−yn)⎦⎥⎥⎤，b=⎣⎢⎢⎡x12−xn2+y12−yn2−d12+dn2x22−xn2+y22−yn2−d22+dn2……xn−12−xn2+yn−12−yn2−dn−12+dn2⎦⎥⎥⎤，X=[xy]
通过标准最小均方差估计可以计算得出未知节点D的坐标： X ^ = ( A T A ) − 1 A T b \hat{X} = (A^TA)^{-1}A^Tb X^=(ATA)−1ATb
扫一扫
3127
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
