波束空间 MIMO （二）

波束空间 MIMO （二）

A. Saleh-Valenzuela 信道模型

Saleh-Valenzuela 信道模型，简称 S-V信道模型，是一个室内多径信道统计模型。目前 IEEE 802.15.3c 协议所使用的标准信道模型，即为经过扩充后的 S-V 信道模型。
考虑时不变信道，首先定义阵列响应向量：
a ( θ ) = 1 N [ exp ⁡ ( − j 2 π θ v ) ] v ∈ { i − N − 1 2 ;   i = 0 , 1 , . . . , N − 1 } \mathbf a(\theta) = \frac{1}{\sqrt N} \Big[\exp(-j 2\pi \theta v)\Big]_{\large{ v \in \{ i -\frac{N - 1}{2}; \ i = 0,1,...,N - 1\} }} a(θ)=N ​1​[exp(−j2πθv)]v∈{i−2N−1​; i=0,1,...,N−1}​
这里 $\mathbf{a}(\theta )\in {\mathbb{C}}^{N\times 1}$。
索引内容如下：
v ∈ { − N − 1 2 , − N − 3 2 , ⋯   , 0 , ⋯   , N − 3 2 , N − 1 2 } v \in \{ -\frac{N - 1}{2}, -\frac{N - 3}{2}, \cdots, 0, \cdots, \frac{N - 3}{2}, \frac{N - 1}{2}\} v∈{−2N−1​,−2N−3​,⋯,0,⋯,2N−3​,2N−1​}
且由于 $d=0.5\lambda$，$\theta =\frac{d\sin \varphi }{\lambda }=\frac{\sin \varphi }{2}$。如下图，注意 $\varphi \in [-\pi /2,\pi /2]$。

移动用户 $k$ 的的接收信号经历的信道向量为 $\mathbf{H}$ 矩阵中的第 $k$ 列 ${\mathbf{h}}_k$，相当于 MISO 系统。由于在毫米波频率下传播的高度定向和准光学性质，LoS（Line-of-Sight）直射传播是主要的传播方式，且可能存在多径分量。可以推出 S-V 信道模型中第 $k$ 个用户的 MP（Multipath）多径分量的信道向量为
$${\mathbf{h}}_k={\beta }_{k,0}\mathbf{a}({\theta }_{k,0})+\sum _{i=1}^L{\beta }_{k,i}\mathbf{a}({\theta }_{k,i})$$
这里公式第一项代表 LOS 成分，${\beta }_{k,i}$ 表示第 $k$ 个用户第 $i$ 条 NLOS 路径对应的路径损耗。$L$ 是 NLOS 路径数目。多径分量的幅度 $|{\beta }_{k,i}|$ 通常比 LoS 成分 $|{\beta }_{k,0}|$ 小 5 到 10 dB。

---

B. 波束空间信道表示

根据阵列响应向量 $\mathbf{a}({\theta }_{k,i})$，可以构造酉矩阵 $\mathbf{U}$（预定义的空间方向）。矩阵 $\mathbf{U}$ 的列对应了 $N$ 个固定空间频率/角度的阵列响应向量（覆盖了整个空间的 $N$ 个正交阵列导向矢量，作用是移动做内积即卷积，映射到稀疏的最大的几个方向），如下：
$$\mathbf{U}={\left[\mathbf{a}({\bar{\theta }}_1),\mathbf{a}({\bar{\theta }}_2),\cdots ,\mathbf{a}({\bar{\theta }}_N)\right]}^{\mathrm{H}}$$
其中
θ ˉ n = 1 N ( n − N − 1 2 ) ,    n ∈ { 0 , 1 , 2 , ⋯   , ( N − 1 ) } \bar{\theta}_n = \frac{1}{N} \left(n-\frac{N-1}{2} \right),\ \ n \in \{0,1,2,\cdots,(N-1)\} θˉn​=N1​(n−2N−1​),  n∈{0,1,2,⋯,(N−1)}
等价于如下形式：
θ ˉ n = 1 N ( n − N + 1 2 ) ,    n ∈ { 1 , 2 , ⋯   , N } \bar{\theta}_n = \frac{1}{N} \left(n-\frac{N+1}{2} \right),\ \ n \in \{1,2,\cdots,N\} θˉn​=N1​(n−2N+1​),  n∈{1,2,⋯,N}
且该形式在论文中更为常见。
索引内容如下：
N θ ˉ ∈ { − N − 1 2 , − N − 3 2 , ⋯   , 0 , ⋯   , N − 3 2 , N − 1 2 } N\bar{\theta} \in \{ -\frac{N - 1}{2}, -\frac{N - 3}{2}, \cdots, 0, \cdots, \frac{N - 3}{2}, \frac{N - 1}{2}\} Nθˉ∈{−2N−1​,−2N−3​,⋯,0,⋯,2N−3​,2N−1​}
至此，即可完成对 S-V 模型的波束空间转换。将信道矩阵变换到角域下，然后可以利用波束选择算法的基础就是波束空间下的信道矩阵具有稀疏性。

已知波束空间表示为 $\tilde{\mathbf{H}}=\mathbf{U}\mathbf{H}$，我们对于 ${\tilde{\mathbf{h}}}_k$ 用户向量的第 $n$ 元素 ${\tilde{\mathbf{h}}}_{k,n}$ 进行研究：

h ~ k = U h k = [ a ( θ ˉ 1 ) , a ( θ ˉ 2 ) , ⋯   , a ( θ ˉ N ) ] H ∑ i = 0 L β k , i a ( θ k , i ) = [ a H ( θ ˉ 1 ) a H ( θ ˉ 2 ) ⋮ a H ( θ ˉ N ) ] ∑ i = 0 L β k , i a ( θ k , i ) J = { v − N − 1 2 ;   v = 0 , 1 , . . . , N − 1 } h ~ k , n = a H ( θ ˉ n ) ∑ i = 0 L β k , i a ( θ k , i ) = 1 N ∑ i = 0 L β k , i exp ⁡ ( + j 2 π θ ˉ n J ) exp ⁡ ( − j 2 π θ k , i J ) = 1 N ∑ i = 0 L β k , i ∑ v ∈ J exp ⁡ [ − j 2 π ( θ k , i − θ ˉ n ) v ] = 1 N ∑ i = 0 L β k , i sin ⁡ ( π N ( θ k , i − θ ˉ n ) ) sin ⁡ ( π ( θ k , i − θ ˉ n ) ) = 1 N ∑ i = 0 L β k , i Υ ( θ k , i − θ ˉ n ) = 1 N ∑ i = 0 L β k , i Υ N ( θ ˉ n − θ k , i ) \begin{aligned} \widetilde{\mathbf h}_{k} &= \mathbf U\mathbf h_k \\ &= \left[\mathbf {a}(\bar{\theta}_1),\mathbf {a}(\bar{\theta}_2),\cdots,\mathbf {a}(\bar{\theta}_N) \right]^{\rm H} \sum_{i=0}^{L} \beta_{k,i} \mathbf{ \large a}(\theta_{k,i}) \\ &=\begin{bmatrix} \mathbf {a}^{\rm H}(\bar{\theta}_1)\\ \mathbf {a}^{\rm H}(\bar{\theta}_2)\\ \vdots \\ \mathbf {a}^{\rm H}(\bar{\theta}_N) \end{bmatrix}\sum_{i=0}^{L} \beta_{k,i} \mathbf{ \large a}(\theta_{k,i}) \\ \\ \mathcal J &= \{ v -\frac{N - 1}{2}; \ v= 0,1,...,N - 1\} \\ \\ \widetilde{\mathbf h}_{k,n} &=\mathbf {a}^{\rm H}(\bar{\theta}_n)\sum_{i=0}^{L} \beta_{k,i} \mathbf{ \large a}(\theta_{k,i}) \\ &=\frac{1}{N}\sum_{i=0}^{L} \beta_{k,i} \exp(+j 2\pi \bar{\theta}_n \mathcal J) \exp(-j 2\pi \theta_{k,i} \mathcal J)\\ &=\frac{1}{N}\sum_{i=0}^{L} \beta_{k,i} \sum_{v \in \mathcal J}\exp\bigg[ -j 2\pi \Big(\theta_{k,i}-\bar{\theta}_n \Big) v\bigg] \\ &=\frac{1}{N}\sum_{i=0}^{L} \beta_{k,i} \frac{\sin \Big(\pi N(\theta_{k,i}-\bar{\theta}_n)\Big)} {\sin \Big(\pi (\theta_{k,i}-\bar{\theta}_n)\Big)} \\ &=\frac{1}{N}\sum_{i=0}^{L} \beta_{k,i} \Upsilon(\theta_{k,i}-\bar{\theta}_n) =\frac{1}{N}\sum_{i=0}^{L} \beta_{k,i} \Upsilon_N(\bar{\theta}_n-\theta_{k,i}) \end{aligned} h k​Jh k,n​​=Uhk​=[a(θˉ1​),a(θˉ2​),⋯,a(θˉN​)]Hi=0∑L​βk,i​a(θk,i​)=⎣⎢⎢⎢⎡​aH(θˉ1​)aH(θˉ2​)⋮aH(θˉN​)​⎦⎥⎥⎥⎤​i=0∑L​βk,i​a(θk,i​)={v−2N−1​; v=0,1,...,N−1}=aH(θˉn​)i=0∑L​βk,i​a(θk,i​)=N1​i=0∑L​βk,i​exp(+j2πθˉn​J)exp(−j2πθk,i​J)=N1​i=0∑L​βk,i​v∈J∑​exp[−j2π(θk,i​−θˉn​)v]=N1​i=0∑L​βk,i​sin(π(θk,i​−θˉn​))sin(πN(θk,i​−θˉn​))​=N1​i=0∑L​βk,i​Υ(θk,i​−θˉn​)=N1​i=0∑L​βk,i​ΥN​(θˉn​−θk,i​)​
其中，${{\rm Y}}_N(t)=\frac{\sin (\pi Nt)}{\sin (\pi t)}$ 是 Dirichlet sinc function（偶函数性质）。
图像为 $N=10$ 的例子：

这里有对于该函数性质的图例（$N$ 取偶数和奇数的图像趋势不同）：

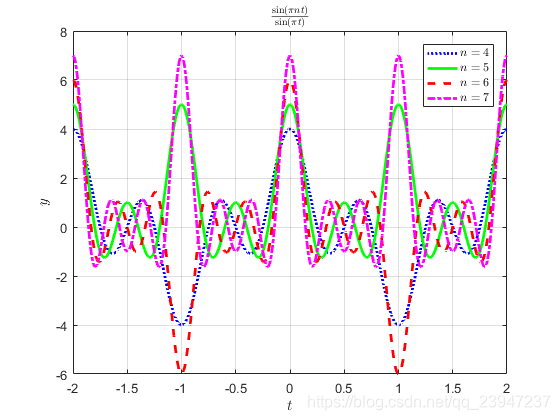
我们发现，当 $N$ 是奇数时，函数是 $t$ 的周期函数，且 $t$ 的周期为 $T=1$。

B. 实验仿真

下面对 mmWave Beamspace MIMO 信道矩阵进行仿真分析。
首先给出实验参数设置：

• 发射端有 $N=64$ 根天线
• 存在 $K=16$ 个用户
• 多径条数为 $L=2$
• LOS 以及 NLOS 对应的信道衰减 ${\beta }_{k,0}\sim \mathcal{C}\mathcal{N}(0,1)$，${\beta }_{k,i}\sim \mathcal{C}\mathcal{N}(0,10^{-1})$
• LOS 以及 NLOS 对应的角度参数服从相同的均匀分布 $\theta \sim \text{U}(-\frac{1}{2},\frac{1}{2})$
• 信噪比 $\text{SNR}=30\text{dB}$

效果如下：

• 原始信道矩阵
  
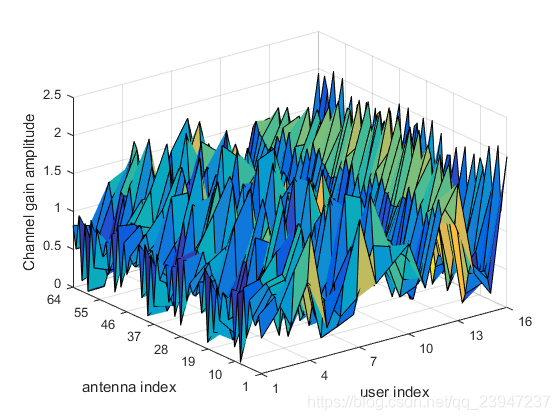
• 波束空间信道矩阵
  

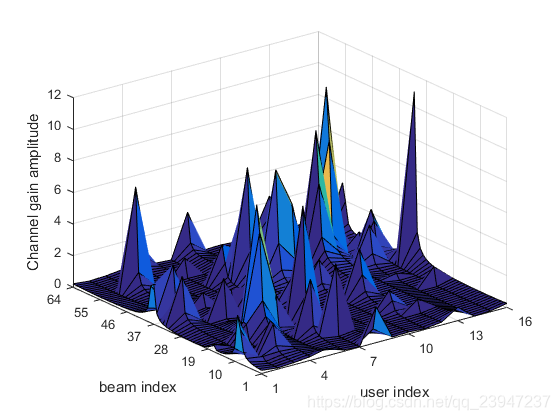
由图可知，物理空间下的信道矩阵是不具备稀疏性的。信道矩阵转换到波束空间后，幅值呈离散的尖状，也就是说波束空间下信道矩阵是稀疏的。所以可以选择发送部分波束，仅发送幅值对应为尖状处的波束序号对应的波束即可，这也就是波束选择的概念。